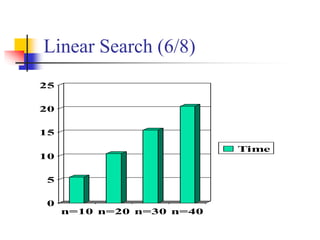
This document contains a lecture on various searching algorithms, including linear search, binary search, and interpolation search. It provides descriptions of each algorithm, pseudocode, examples, and complexity analyses. Linear search has a complexity of O(n) but is simple to implement. Binary search has a better complexity of O(log n) but requires the list to be sorted. Interpolation search has an even better complexity of O(log log n) when values are evenly distributed.







![Linear Search-Pseudo Code (2/8)
LINEAR_SEARCH(A,v)
1. for i←1 to n
2. do if A[i]=v
3. then return I
4. return NIL
DSAL-4,P-13](https://image.slidesharecdn.com/chapter11ds-190904110931/85/Chapter-11-ds-8-320.jpg)










![Binary Search-Pseudo Code-1
(6/10)
RECURSIVE_BINARY _SEARCH (A, v, low, high )
1. if low > high
2. then return NIL
3. mid ←
4. If v = A[mid]
5. then return mid
6. If v > A[mid]
7. then return RECURSIVE_BINARY _SEARCH (A, v, mid+1, high )
8. else return RECURSIVE_BINARY _SEARCH (A, v, low, mid-1)
DSAL-4,P-18
( )/2low high ](https://image.slidesharecdn.com/chapter11ds-190904110931/85/Chapter-11-ds-20-320.jpg)
![Binary Search-Pseudo Code-2
(7/10)
ITERATIVE_BINARY _SEARCH (A, v, low, high )
1. While low high
2. do mid ←
3. If v = A[mid]
4. then return mid
5. else if v > A[mid]
6. then low ← mid+1
7. else high← mid-1
8. return NIL
DSAL-4,P-18
( )/2low high
](https://image.slidesharecdn.com/chapter11ds-190904110931/85/Chapter-11-ds-21-320.jpg)




![Interpolation Search
Interpolation is the process of using known
values to guess where an unknown value lies.
We use the indexes of known values in the
list to guess what index the target value
should have.
Interpolation search selects the dividing point
by interpolation using the following code
m = l + (x – A[l])*(r-l)/(A[r]-A[l])](https://image.slidesharecdn.com/chapter11ds-190904110931/85/Chapter-11-ds-26-320.jpg)

![Interpolation Search
Compare x to A[m]
If x = A[m]: Found.
If x<A[m]: set r = m-1
If x > A[m]: set l = m + 1
If searching is still not finish, continue searching
with new l and r.
Stop searching when Found or x<A[l] or x>A[r].
D:Data StructuresHanif_SearchSearchingLecture 08 - Searching Algorithms.ppt](https://image.slidesharecdn.com/chapter11ds-190904110931/85/Chapter-11-ds-29-320.jpg)
![Interpolation Search
Example: Find the key x = 32 in the list
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 4 7 9 9 12 13 17 19 21 24 32 36 44 45 54 55 63 66 70
1: l=1, r=20 -> m=1+(32-1)*(20-1)/(70-1) = 10
a[10]=21<32=x -> l=11
2: l=11, r=20 -> m=11+(30-24)*(20-11)/(70-24) = 12
a[12]=32=x -> Found at m = 12](https://image.slidesharecdn.com/chapter11ds-190904110931/85/Chapter-11-ds-30-320.jpg)
![Interpolation Search
Example: Find the key x = 30 in the list
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 4 7 9 9 12 13 17 19 21 24 32 36 44 45 54 55 63 66 70
1: l=1, r=20 -> m=1+(30-1)*(20-1)/(70-1) = 9
a[9]=19<30=x -> l=10
2: l=10, r=20 -> m=10+(30-21)*(20-10)/(70-21) = 12
a[12]=32>30=x -> r = 11
3: l=10, r=11 -> m=10+(30-24)*(11-10)/(24-21) = 12
m=12>11=r: Not Found](https://image.slidesharecdn.com/chapter11ds-190904110931/85/Chapter-11-ds-31-320.jpg)
![Interpolation Search-Pseudo
Code (1/2)
Private Sub Interpolation(a[]: Int, x: Int, n: Int,
Found: Boolean)
l = 1: r = n
Do While (r > l)
m = l + ((x – a[l]) / (a[r] – a[l])) * (r - l)
‘Verify and Decise What to do next
Loop
End Sub](https://image.slidesharecdn.com/chapter11ds-190904110931/85/Chapter-11-ds-32-320.jpg)
![Interpolation Search-Pseudo
Code (2/2)
‘Verify and Decide what to do next
If (a[m] = x) Or (m < l) Or (m > r) Then
Found = iif(a[m] = x, True, False)
Exit Do
ElseIf (a[m] < x) Then
l = m + 1
ElseIf (a[m] > x) Then
r = m – 1
End If](https://image.slidesharecdn.com/chapter11ds-190904110931/85/Chapter-11-ds-33-320.jpg)

