Heapsort is a sorting algorithm with average-case time complexity of O(n log n). It works by first constructing a max-heap from the input array and then extracting elements from the heap and placing them in sorted order in the array. The key procedures are MAX-HEAPIFY, which maintains the heap property by floating elements down the heap, and BUILD-MAX-HEAP, which constructs a max-heap from an unsorted array in linear time O(n) by calling MAX-HEAPIFY on successive subtrees.

1. Chapter 10
Heapsort
Dr. Muhammad Hanif Durad
Department of Computer and Information Sciences
Pakistan Institute Engineering and Applied Sciences
hanif@pieas.edu.pk
Some slides have bee adapted with thanks from some other lectures
available on Internet. It made my life easier, as life is always
miserable at PIEAS (Sir Muhammad Yusaf Kakakhil )

2. Dr. Hanif Durad 2
Lecture Outline
 Heap
 Binary Heap
 Heap Property
 Building A Heap
 The HeapSort Algorithm

3. Introduction
 Heapsort
 Running time: O(n lg n)
 Like merge sort
 Sort in place: only a constant number of array elements are
stored outside the input array at any time
 Like insertion sort
 Heap
 A data structure used by Heapsort to manage information
during the execution of the algorithm
 Can be used as an efficient priority queue
D:DSAL5165 Advanced Algorithm and Programming Languageunit06.ppt

4. Binary Heap
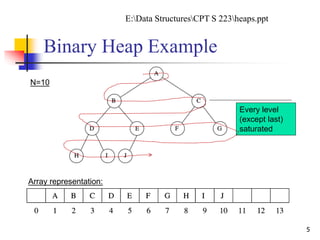
 A heap can be seen as a complete binary tree
 The tree is completely filled on all levels except possibly the
lowest.
 In practice, heaps are usually implemented as arrays
 An array A that represent a heap is an object with two attributes:
A[1 .. length[A]]
 length[A]: # of elements in the array
 heap-size[A]: # of elements in the heap stored within array A, where heap-
size[A] ≤ length[A]
 No element past A[heap-size[A]] is an element of the heap
 max-heap and min-heap
16 14 10 8 7 9 3 2 4 1A =
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

5. Binary Heap Example
5
Every level
(except last)
saturated
Array representation:
N=10
E:Data StructuresCPT S 223heaps.ppt

6. A Max-Heap
D:DSAL5165 Advanced Algorithm and Programming Languageunit06.ppt

7. 7
Referencing Heap Elements
 The root node is A[1]
 Node i is A[i]
 Parent(i)
 return i/2
 Left(i)
 return 2*i
 Right(i)
 return 2*i + 1
1 2 3 4 5 6 7 8 9 10
16 15 10 8 7 9 3 2 4 1
Level: 3 2 1 0
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

8. Heap Property
 Heap property – the property that the values in the node
must satisfy
 Max-heap property: for every node i other than the root
 A[PARENT(i)]  A[i]
 The value of a node is at most the value of its parent
 The largest element in a max-heap is stored at the root
 The subtree rooted at a node contains values on larger than that
contained at the node itself
 Min-heap property: for every node i other than the root
 A[PARENT(i)]  A[i]
D:DSAL5165 Advanced Algorithm and Programming Languageunit06.ppt

9. Heap Height
 The height of a node in a heap is the number of edges on the
longest simple downward path from the node to a leaf
 The height of a heap is the height of its root
 The height of a heap of n elements is (lg n)
D:DSAL5165 Advanced Algorithm and Programming Languageunit06.ppt

10. 10
# of nodes in each level
 Fact: an n-element heap has at most 2h-k nodes of level k,
where h is the height of the tree
 for k = h (root level)  2h-h = 20 = 1
 for k = h-1  2h-(h-1) = 21 = 2
 for k = h-2  2h-(h-2) = 22 = 4
 for k = h-3  2h-(h-3) = 23 = 8
 …
 for k = 1  2h-1 = 2h-1
 for k = 0 (leaves level) 2h-0 = 2h
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

11. 11
Heap Height
 A heap storing n keys has height h = lg n = (lg n)
 Due to heap being complete, we know:
 The maximum # of nodes in a heap of height h
 2h + 2h-1 + … + 22 + 21 + 20 =
  i=0 to h 2i=(2h+1–1)/(2–1) = 2h+1 - 1
 The minimum # of nodes in a heap of height h
 1 + 2h-1 + … + 22 + 21 + 20 =
  i=0 to h-1 2i + 1 = (2h-1+1–1)/(2–1) + 1 = 2h
 Therefore
 2h  n  2h+1 - 1
 h  lg n & lg(n+1) – 1  h
 lg(n+1) – 1  h  lg n
 which in turn implies:
 h = lg n = (lg n)
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

12. Heap Procedures
 MAX-HEAPIFY: maintain the max-heap property
 O(lg n)
 BUILD-MAX-HEAP: produces a max-heap from an unordered
input array
 O(n)
 HEAPSORT: sorts an array in place
 O(n lg n)
 MAX-HEAP-INSERT, HEAP-EXTRACT, HEAP-INCREASE-
KEY, HEAP-MAXIMUM: allow the heap data structure to be
used as a priority queue
 O(lg n)
D:DSAL5165 Advanced Algorithm and Programming Languageunit06.ppt

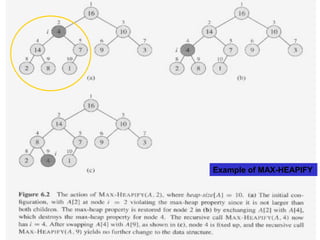
13. Maintaining the Heap Property
 MAX-HEAPIFY
 Inputs: an array A and an index i into the array
 Assume the binary tree rooted at LEFT(i) and
RIGHT(i) are max-heaps, but A[i] may be smaller
than its children (violate the max-heap property)
 MAX-HEAPIFY let the value at A[i] floats down in
the max-heap
IA, P-130 Solved in notes
DSALN1-1, P-21
D:DSAL5165 Advanced Algorithm and Programming Languageunit06.ppt

14. MAX-HEAPIFY
Extract the indices of LEFT and RIGHT
children of i
Choose the largest of A[i], A[l], A[r]
Float down A[i] recursively
D:DSAL5165 Advanced Algorithm and Programming Languageunit06.ppt

15. 15
MAX-HEAPIFY Example
16
4 10
14 7 9 3
2 8 1
16 4 10 14 7 9 3 2 8 1A =
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

16. 16
16
4 10
14 7 9 3
2 8 1
16 10 14 7 9 3 2 8 1A = 4
MAX-HEAPIFY Example
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

17. 17
16
4 10
14 7 9 3
2 8 1
16 10 7 9 3 2 8 1A = 4 14
MAX-HEAPIFY Example
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

18. 18
16
14 10
4 7 9 3
2 8 1
16 14 10 4 7 9 3 2 8 1A =
MAX-HEAPIFY Example
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

19. 19
16
14 10
4 7 9 3
2 8 1
16 14 10 7 9 3 2 8 1A = 4
MAX-HEAPIFY Example
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

20. 20
16
14 10
4 7 9 3
2 8 1
16 14 10 7 9 3 2 1A = 4 8
MAX-HEAPIFY Example
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

21. 21
16
14 10
8 7 9 3
2 4 1
16 14 10 8 7 9 3 2 4 1A =
MAX-HEAPIFY Example
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

22. 22
16
14 10
8 7 9 3
2 4 1
16 14 10 8 7 9 3 2 1A = 4
MAX-HEAPIFY Example
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

23. 23
16
14 10
8 7 9 3
2 4 1
16 14 10 8 7 9 3 2 4 1A =
MAX-HEAPIFY Example
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

24. Example of MAX-HEAPIFY

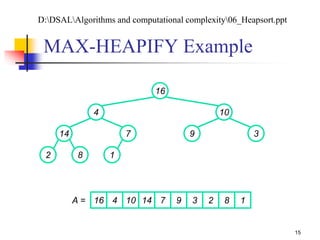
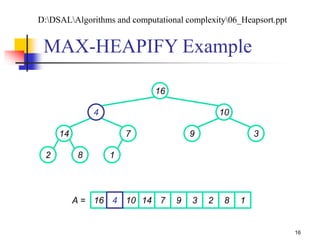
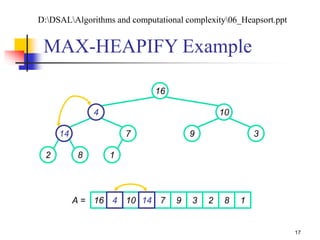
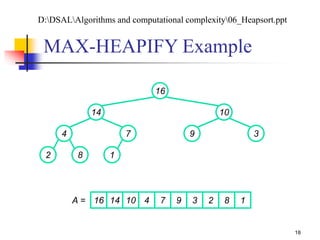
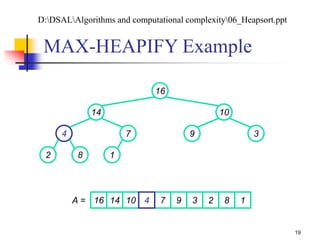
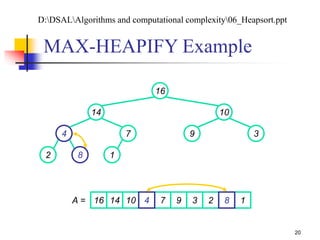
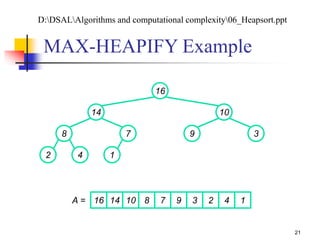
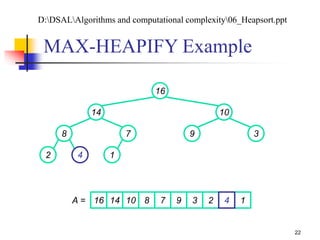
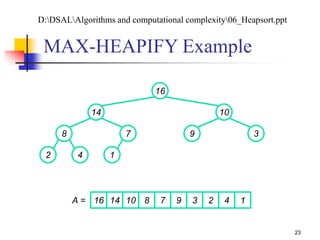
25. Analyzing MAX-HEAPIFY (1/2)
 (1) to find out the largest among A[i], A[LEFT(i)], and
A[RIGHT(i)]
 Plus the time to run MAX-HEAPIFY on a subtree rooted
at one of the children of node i
 The children’s subtrees each have size at most 2n/3 – the worst
case occurs when the last row of the tree is exactly half full
 T(n)  T(2n/3) + (1)
 By case 2 of the master theorem: T(n) = O(lg n)
D:DSAL5165 Advanced Algorithm and Programming Languageunit06.ppt

26. Analyzing MAX-HEAPIFY (2/2)
 Alternately, Heapify takes T(n) = Θ(h)
 h = height of heap = lg n
 T(n) = Θ(lg n)
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

27. Building A Heap

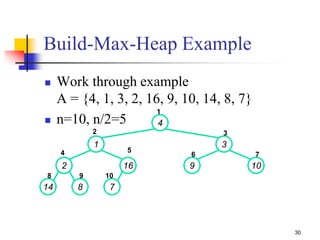
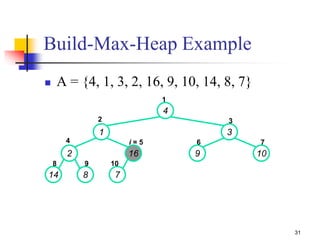
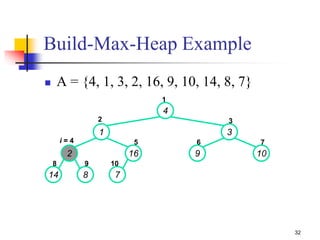
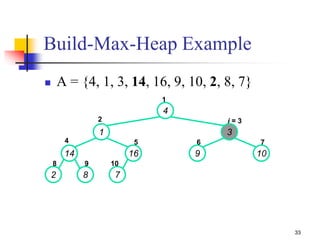
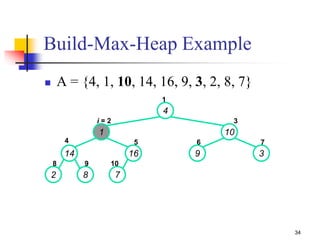
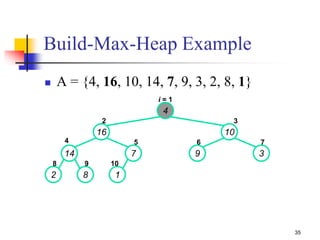
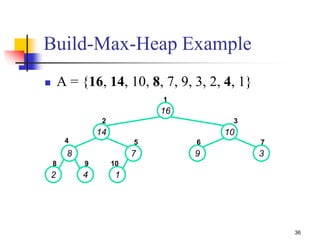
28. Build-Max-Heap (1/2)
 We can build a heap in a bottom-up manner by running
Build-Max-Heap() on successive subarrays
 Fact: for array of length n, all elements in range
A[n/2 + 1, n/2 + 2 .. n] are heaps (Why?)
 These elements are leaves, they do not have children
 We also know that the leave-level has at most 2h nodes = n/2
nodes
 and other levels have a total of n/2 nodes
 Walk backwards through the array from n/2 to 1, calling
Build-Max-Heap() on each node.
D:DSALAlgorithms and computational complexity06_Heapsort.ppt
IA, P-133

29. Build-Max-Heap (2/2)
// given an unsorted array A, make A a heap
 The Build-Max-Heap () procedure, which runs in linear time,
produces a max-heap from an unsorted input array.
 However, the MAX-HEAPIFY() procedure, which runs in
O(lg n) time, is the key to maintaining the heap property.
D:DSALAlgorithms and computational complexity06_Heapsort.ppt
IA, P-133

30. 30
Build-Max-Heap Example
 Work through example
A = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7}
 n=10, n/2=5 4
1 3
2 16 9 10
14 8 7
1
2 3
4 5
6 7
8 9 10

31. 31
 A = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7}
4
1 3
2 16 9 10
14 8 7
1
2 3
4 i = 5 6 7
8 9 10
Build-Max-Heap Example

32. 32
 A = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7}
4
1 3
2 16 9 10
14 8 7
1
2 3
i = 4 5 6 7
8 9 10
Build-Max-Heap Example

33. 33
 A = {4, 1, 3, 14, 16, 9, 10, 2, 8, 7}
4
1 3
14 16 9 10
2 8 7
1
2 i = 3
4 5 6 7
8 9 10
Build-Max-Heap Example

34. 34
 A = {4, 1, 10, 14, 16, 9, 3, 2, 8, 7}
4
1 10
14 16 9 3
2 8 7
1
i = 2 3
4 5 6 7
8 9 10
Build-Max-Heap Example

35. 35
 A = {4, 16, 10, 14, 7, 9, 3, 2, 8, 1}
4
16 10
14 7 9 3
2 8 1
i = 1
2 3
4 5 6 7
8 9 10
Build-Max-Heap Example

36. 36
 A = {16, 14, 10, 8, 7, 9, 3, 2, 4, 1}
16
14 10
8 7 9 3
2 4 1
1
2 3
4 5 6 7
8 9 10
Build-Max-Heap Example

37. 16 14 10 8 7 9 3 2 1A = 4

38. 38
Analyzing Build-Max-Heap (1/2)
 Each call to MAX-HEAPIFY takes O(lg n) time
 There are O(n) such calls (specifically, n/2)
 Thus the running time is O(n lg n)
 Is this a correct asymptotic upper bound?
 YES
 Is this an asymptotically tight bound?
 NO
 A tighter bound is O(n)
 How can this be? Is there a flaw in the above reasoning?
 We can derive a tighter bound by observing that the time for MAX-HEAPIFY
to run at a node varies with the height of the node in the tree, and the heights of
most nodes are small.
 Fact: an n-element heap has at most 2h-k nodes of level k, where h is
the height of the tree.
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

39. 39
 The time required by MAX-HEAPIFY on a node of height k is O(k). So we
can express the total cost of Build-Max-Heap as
k=0 to h 2h-k O(k) = O(2h k=0 to h k/2k)
= O(n k=0 to h k(½)k)
From: k=0 to ∞ k xk = x/(1-x)2 where x =1/2
So, k=0 to  k/2k = (1/2)/(1 - 1/2)2 = 2
Therefore, O(n k=0 to h k/2k) = O(n)
 So, we can bound the running time for building a heap from an
unordered array in linear time
Analyzing Build-Max-Heap (2/2)
IA, P-135
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

40. The HeapSort Algorithm

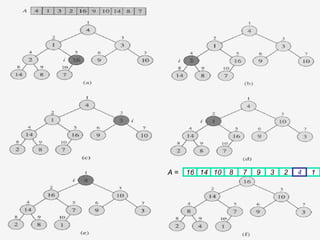
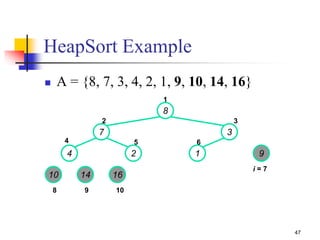
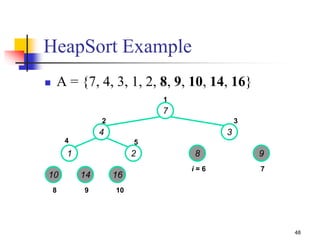
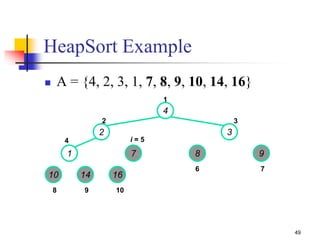
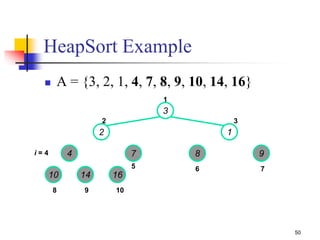
41. 41
Heapsort
 Given Build-Max-Heap an in-place sorting
algorithm is easily constructed:
 Maximum element is at A[1]
 Discard by swapping with element at A[n]
 Decrement heap_size[A]
 A[n] now contains correct value
 Restore heap property at A[1] by calling MAX-
HEAPIFY
 Repeat, always swapping A[1] for
A[heap_size(A)]

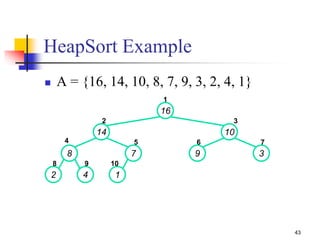
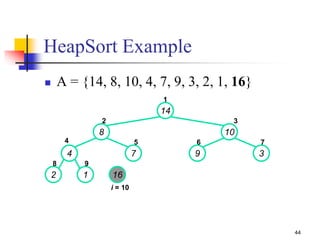
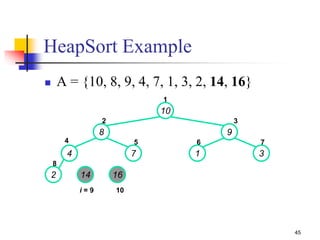
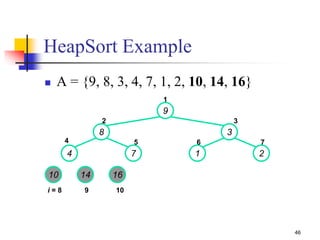
42. 42
HEAPSORT(A)
{
1. Build-MAX-Heap(A)
2. for i  length[A] downto 2
3. do exchange A[1]  A[i]
4. heap-size[A]  heap-size[A] - 1
5. MAX- Heapify(A, 1)
}
Heapsort

43. 43
HeapSort Example
 A = {16, 14, 10, 8, 7, 9, 3, 2, 4, 1}
16
14 10
8 7 9 3
2 4 1
1
2 3
4 5 6 7
8 9 10

44. 44
 A = {14, 8, 10, 4, 7, 9, 3, 2, 1, 16}
14
8 10
4 7 9 3
2 1 16
1
2 3
4 5 6 7
8 9
i = 10
HeapSort Example

45. 45
 A = {10, 8, 9, 4, 7, 1, 3, 2, 14, 16}
10
8 9
4 7 1 3
2 14 16
1
2 3
4 5 6 7
8
10i = 9
HeapSort Example

46. 46
 A = {9, 8, 3, 4, 7, 1, 2, 10, 14, 16}
9
8 3
4 7 1 2
10 14 16
1
2 3
4 5 6 7
9 10i = 8
HeapSort Example

47. 47
 A = {8, 7, 3, 4, 2, 1, 9, 10, 14, 16}
8
7 3
4 2 1 9
10 14 16
1
2 3
4 5 6
8 9 10
i = 7
HeapSort Example

48. 48
 A = {7, 4, 3, 1, 2, 8, 9, 10, 14, 16}
7
4 3
1 2 8 9
10 14 16
1
2 3
4 5
7
8 9 10
i = 6
HeapSort Example

49. 49
 A = {4, 2, 3, 1, 7, 8, 9, 10, 14, 16}
4
2 3
1 7 8 9
10 14 16
1
2 3
4
6 7
8 9 10
i = 5
HeapSort Example

50. 50
 A = {3, 2, 1, 4, 7, 8, 9, 10, 14, 16}
3
2 1
4 7 8 9
10 14 16
1
2 3
5 6 7
8 9 10
i = 4
HeapSort Example

51. 51
 A = {2, 1, 3, 4, 7, 8, 9, 10, 14, 16}
2
1 3
4 7 8 9
10 14 16
1
2
4
5 6 7
8 9 10
i = 3
HeapSort Example

52. 52
 A = {1, 2, 3, 4, 7, 8, 9, 10, 14, 16}
1
2 3
4 7 8 9
10 14 16
1
3
4
5 6 7
8 9 10
i =2
HeapSort Example

53. 53
Analyzing Heapsort (1/2)
 The call to BUILD-MAX-HEAP() takes O(n) time
 Each of the n - 1 calls to MAX- HEAPIFY() takes
O(lg n) time
 Thus the total time taken by HEAPSORT()
= O(n) + (n - 1) O(lg n)
= O(n) + O(n lg n)
= O(n lg n)

54. 54
Analyzing Heapsort (2/2)
 The O(n log n) run time of heap-sort is much better
than the O(n2) run time of selection and insertion sort
 Although, it has the same run time as Merge sort, but
it is better than Merge Sort regarding memory space
 Heap sort is in-place sorting algorithm
 But not stable
 Does not preserve the relative order of elements with equal
keys
 Sorting algorithm (stable) if 2 records with same key stay in
original order

55. Example of HeapSort
Next Slide

56. 14
1
14
10
1
14
10
9
1
Example of HeapSort (Cont.)

57. Priority Queues

58. 58
Max-Priority Queues
 A data structure for maintaining a set S of elements,
each with an associated value called a key.
 Applications:
 scheduling jobs on a shared computer
 prioritizing events to be processed based on their predicted
time of occurrence.
 Printer queue
 Heap can be used to implement a max-priority queue
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

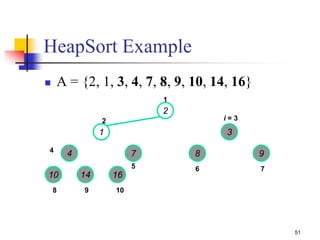
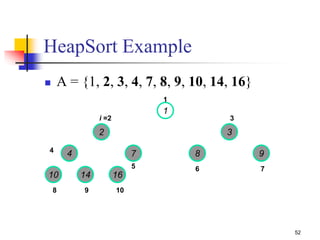
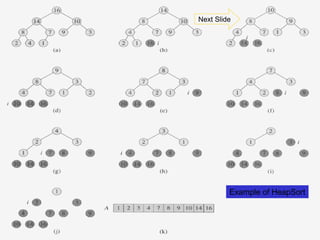
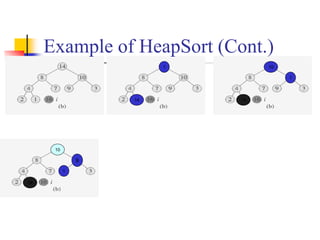
59. 59
Max-Priority Queue: Basic
Operations
 Maximum(S): return A[1]
 returns the element of S with the largest key (value)
 Extract-Max(S):
 removes and returns the element of S with the largest key
 Increase-Key(S, x, k):
 increases the value of element x’s key to the new value k,
x.value  k
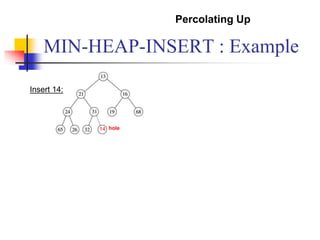
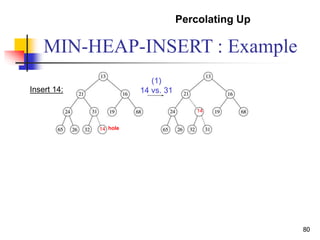
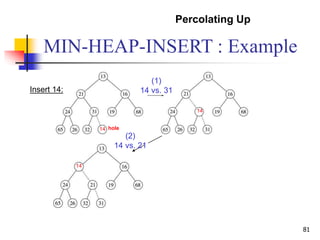
 Insert(S, x):
 inserts the element x into the set S, i.e. S  S  {x}

60. HEAP-MAXIMUM
(1)
D:DSAL5165 Advanced Algorithm and Programming Languageunit06.ppt

61. 61
HEAP-Extract-Max(A)
1. if heap-size[A] < 1 // zero elements
2. then error “heap underflow”
3. max  A[1] // max element in first position
4. A[1]  A[heap-size[A]]
// value of last position assigned to first position
5. heap-size[A]  heap-size[A] – 1
6. Heapify(A, 1)
7. return max
Running time : Dominated by the running time of MaxHeapify
= O(lg n)
D:DSAL5165 Advanced Algorithm and Programming Languageunit06.ppt+
E:DSALCOMP 550-00108-heapsort.ppt

62. HEAP-Extract-MIN(A)
 Write a pseudo-code code similar to HEAP-
Extract-MIN(A)

63. HEAP-Extract-MIN
 Minimum element is always at the root in min-
heap
 Heap decreases by one in size
 Move last element into hole at root
 Percolate down while heap-order property not
satisfied
E:Data StructuresCPT S 223heaps.ppt,P-21

64. HEAP-Extract-MIN : Example
Make this
position
empty
Percolating down…

65. 65
Is 31 > min(14,16)?
•Yes - swap 31 with min(14,16)
Make this
position
empty
Copy 31 temporarily
here and move it down
Percolating down…
HEAP-Extract-MIN : Example

66. Is 31 > min(19,21)?
•Yes - swap 31 with min(19,21)
Percolating down…
31
HEAP-Extract-MIN : Example

67. 67
Is 31 > min(65,26)?
•Yes - swap 31 with min(65,26)
Is 31 > min(19,21)?
•Yes - swap 31 with min(19,21)
Percolating down…
Percolating down…
31
31
HEAP-Extract-MIN : Example

68. Percolating down…
Percolating down…
31
HEAP-Extract-MIN : Example

69. 69
Heap order prop
Structure prop
Percolating down…
31
HEAP-Extract-MIN : Example

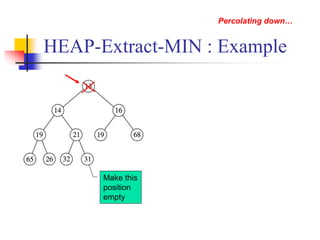
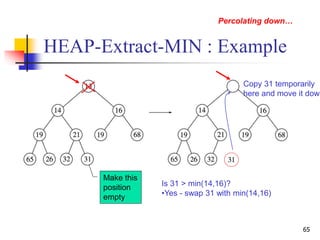
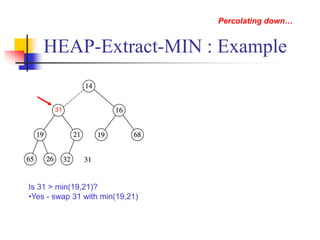
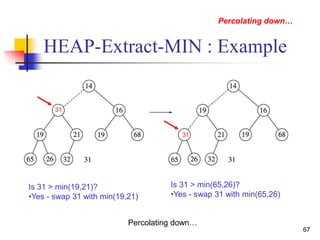
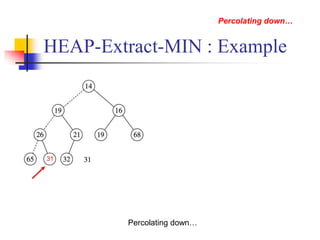
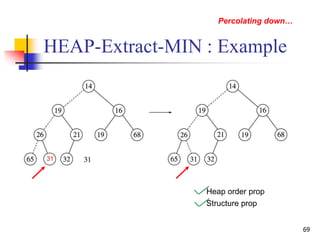
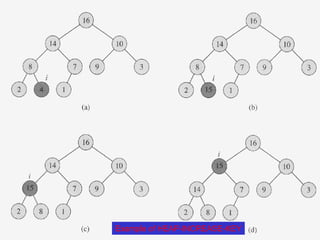
70. HEAP-INCREASE-KEY
 Increase the job priority
 Steps
 Update the key of A[i] to its new value
 May violate the max-heap property
 Traverse a path from A[i] toward the root to find a
proper place for the newly increased key
D:DSAL5165 Advanced Algorithm and Programming Languageunit06.ppt

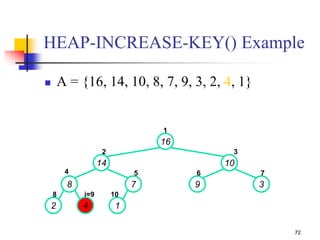
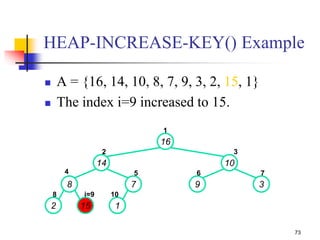
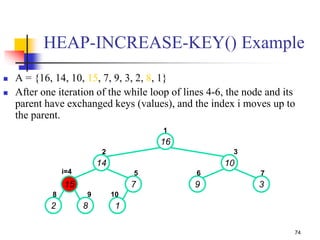
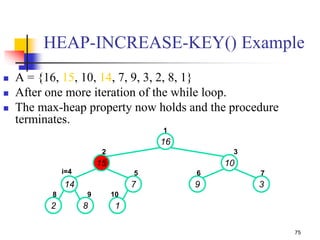
71. 71
HEAP-INCREASE-KEY(A, i, key)
// increase a value (key) in the array
1. if key < A[i]
2. then error “new key is smaller than current key”
3. A[i]  key
4. while i > 1 and A[Parent(i)] < A[i]
5. do exchange A[i]  A[Parent(i)]
6. i  Parent(i) // move index up to parent
O(lg n)
D:DSALAlgorithms and computational complexity06_Heapsort.ppt

72. 72
HEAP-INCREASE-KEY() Example
 A = {16, 14, 10, 8, 7, 9, 3, 2, 4, 1}
16
14 10
8 7 9 3
2 4 1
1
2 3
4 5 6 7
8 i=9 10

73. 73
 A = {16, 14, 10, 8, 7, 9, 3, 2, 15, 1}
 The index i=9 increased to 15.
16
14 10
8 7 9 3
2 15 1
1
2 3
4 5 6 7
8 i=9 10
HEAP-INCREASE-KEY() Example

74. 74
 A = {16, 14, 10, 15, 7, 9, 3, 2, 8, 1}
 After one iteration of the while loop of lines 4-6, the node and its
parent have exchanged keys (values), and the index i moves up to
the parent.
16
14 10
15 7 9 3
2 8 1
1
2 3
i=4 5 6 7
8 9 10
HEAP-INCREASE-KEY() Example

75. 75
 A = {16, 15, 10, 14, 7, 9, 3, 2, 8, 1}
 After one more iteration of the while loop.
 The max-heap property now holds and the procedure
terminates.
16
15 10
14 7 9 3
2 8 1
1
2 3
i=4 5 6 7
8 9 10
HEAP-INCREASE-KEY() Example

76. Example of HEAP-INCREASE-KEY

77. MAX-HEAP-INSERT
O(lg n)
D:DSAL5165 Advanced Algorithm and Programming Languageunit06.ppt+
E:DSALCOMP 550-00108-heapsort.ppt
Running time is O(lg n)
The path traced from the new leaf to the root has
length O(lg n)

78. MIN-HEAP-INSERT
 Insert new element into the heap at the next
available slot (“hole”)
 According to maintaining a complete binary
tree
 Then, “percolate” the element up the heap
while heap-order property not satisfied
78Cpt S 223. School of EECS, WSU
E:Data StructuresCPT S 223heaps.ppt, P-14

79. MIN-HEAP-INSERT : Example
Insert 14:
hole14
Percolating Up

80. 80
Insert 14:
(1)
14 vs. 31
hole
14
Percolating Up
14
MIN-HEAP-INSERT : Example

81. 81
Insert 14:
(1)
14 vs. 31
(2)
14 vs. 21
Percolating Up
hole
14
14
14
MIN-HEAP-INSERT : Example

82. 82
Insert 14:
(1)
14 vs. 31
(3)
14 vs. 13
Heap order prop
Structure prop
hole
14
Percolating Up
14
(2)
14 vs. 21
Path of percolation up
MIN-HEAP-INSERT : Example