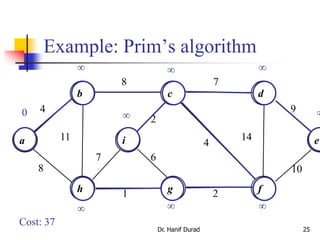
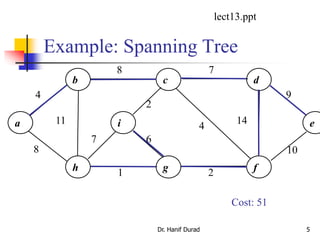
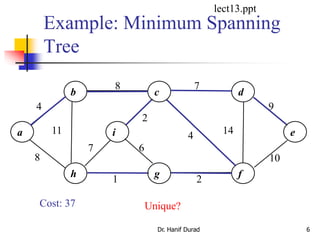
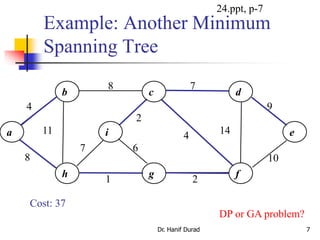
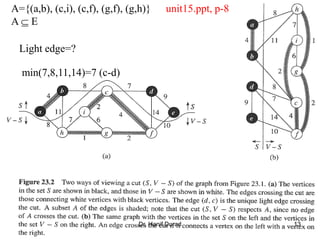
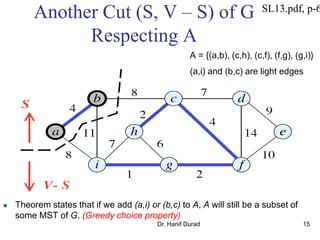
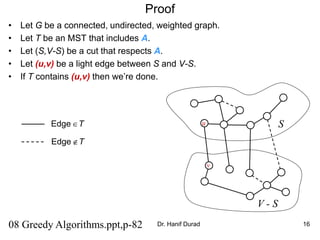
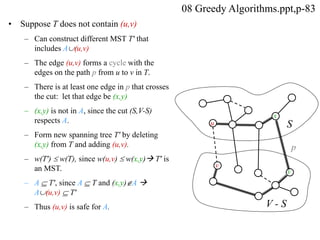
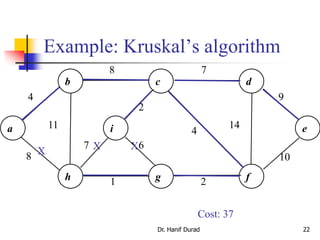
This document summarizes key concepts about minimum spanning trees from a lecture by Dr. Muhammad Hanif Durad. It discusses motivation for finding minimum spanning trees, properties of MSTs, and algorithms like Kruskal's algorithm and Prim's algorithm for finding an MST in polynomial time. Kruskal's algorithm finds the MST by greedily adding the minimum weight edge that connects two components in a forest. Prim's algorithm finds the MST by growing a tree by greedily adding the minimum weight edge connecting the growing tree to a vertex not yet included.

1. Chapter 24
Minimum Spanning Trees
Dr. Muhammad Hanif Durad
Department of Computer and Information Sciences
Pakistan Institute Engineering and Applied Sciences
hanif@pieas.edu.pk
Some slides have bee adapted with thanks from some other lectures
available on Internet. It made my life easier, thanks to Allah
Almighty .

2. Lecture Outline
 Motivation
 Properties of minimum spanning trees
 Kruskal’s algorithm
 Prim’s algorithm
lect13.ppt

3. Facts about (Free) Trees
 A tree with n vertices has exactly n-1 edges
(|E| = |V| - 1)
 There exists a unique path between any two
vertices of a tree
 Adding any edge to a tree creates a unique cycle;
breaking any edge on this cycle restores a tree
For details see CLRS Appendix B.5.1
Dr. Hanif Durad 3
24.ppt, p-7

4. Motivation
 Given a set of nodes and possible connections with weights
between them, find the subset of connections that connects
all the nodes and whose sum of weights is the smallest.
 Examples:
 Communication networks
 Circuit design
 Layout of highway systems
 The nodes and subset of connections form a tree!
 This tree is called the Minimum Spanning Tree (MST)
4
lect13.ppt + 24.ppt, p-1

5. Example: Spanning Tree
Dr. Hanif Durad 5
b c d
h g f
ia e
8 7
1 2
11 14
4
8
7 6
2
4
9
10
Cost: 51
lect13.ppt

6. Example: Minimum Spanning
Tree
Dr. Hanif Durad 6
b c d
h g f
ia e
8 7
1 2
11 14
4
8
7 6
2
4
9
10
Cost: 37
lect13.ppt
Unique?

7. Example: Another Minimum
Spanning Tree
Dr. Hanif Durad 7
b c d
h g f
ia e
8 7
1 2
11 14
4
8
7 6
2
4
9
10
Cost: 37
24.ppt, p-7
DP or GA problem?

8. Optimal Substructure
• Removing one edge (e.g., (c,f)) partitions T into two trees T1 and T2.
 Consider a generic tree T. Let T be the MST of G (other edges of G not shown).
T1 is MST of G1(V1, E1), the subgraph of G induced by the vertices in V1
T2 is MST of G2(V2, E2), the subgraph of G induced by the vertices in V2
Claim
SL13.pdf, p-6
Proof:
 w(T) = w(c,f) + w(T1) + w(T2)
 There can not be better trees than T1 or T2, or T would be suboptimal
Dr. Hanif Durad 8

9. Formal Definition of MST
 Given a connected, undirected, graph G = (V, E), a
spanning tree is an acyclic subset of edges T E that
connects all the vertices together.
 Assuming G is weighted, we define the cost of a
spanning tree T to be the sum of edge weights in the
spanning tree
w(T) = (u,v)T w(u,v)
 A minimum spanning tree (MST) is a spanning tree of
minimum weight.
24.ppt, p-3
Dr. Hanif Durad 9

10. Intuition Behind Greedy MST
 We maintain in a subset of edges A, which will initially
be empty, and we will add edges one at a time, until
equals the MST. We say that a subset A E is viable if
A is a subset of edges in some MST. We say that an
edge (u,v)  E-A is safe if A{(u,v)} is viable.
 Basically, the choice (u,v) is a safe choice to add so that
A can still be extended to form an MST. Note that if A is
viable it cannot contain a cycle. A generic greedy
algorithm operates by repeatedly adding any safe edge to
the current spanning tree.
Dr. Hanif Durad 10
24.ppt, p-8

11. Generic-MST (G, w)
1. A   // A trivially satisfies invariant
// lines 2-4 maintain the invariant
2. while A does not form a spanning tree
3. do find an edge (u,v) that is safe for A
4. A  A  {(u,v)}
5. return A // A is now a MST
Dr. Hanif Durad 11
24.ppt, p-8

12. How to Find A Safe Edge?
 Cut of undirected graph is a partition of its node
set into two parts
 An edge crosses the cut if its endpoints are in
different parts
 A cut respects set of edges A if no edge in A
crosses the cut
 A crossing edge with minimal cost is a light
edge
12
lecture12_minimum_spanning_tree.pdf, p-6
Dr. Hanif Durad

13. Dr. Hanif Durad 13
unit15.ppt, p-8
Light edge=?
min(7,8,11,14)=7 (c-d)
A={(a,b), (c,i), (c,f), (g,f), (g,h)}
A  E

14. Greedy Choice Property
Theorem 23.1:
SL13.pdf, p-7+ 08 Greedy Algorithms.ppt,p-81
 Let
 A be a subset of some MST
 (S,V-S) be a cut that respects A
 (u,v) be a light edge crossing (S,V-S)
 Then
 (u,v) is safe for A.
A
Basis for a greedy algorithm 14Dr. Hanif Durad

15. Another Cut (S, V – S) of G
Respecting A
A = {(a,b), (c,h), (c,f), (f,g), (g,i)}
SL13.pdf, p-6
 Theorem states that if we add (a,i) or (b,c) to A, A will still be a subset of
some MST of G. (Greedy choice property)
(a,i) and (b,c) are light edges
15Dr. Hanif Durad

16. Proof
• Let G be a connected, undirected, weighted graph.
• Let T be an MST that includes A.
• Let (S,V-S) be a cut that respects A.
• Let (u,v) be a light edge between S and V-S.
• If T contains (u,v) then we’re done.
u
v
S
V - S
Edge T
Edge T
16Dr. Hanif Durad08 Greedy Algorithms.ppt,p-82

17. u
x
v
y
S
V - S
• Suppose T does not contain (u,v)
– Can construct different MST T' that
includes A(u,v)
– The edge (u,v) forms a cycle with the
edges on the path p from u to v in T.
– There is at least one edge in p that crosses
the cut: let that edge be (x,y)
– (x,y) is not in A, since the cut (S,V-S)
respects A.
– Form new spanning tree T' by deleting
(x,y) from T and adding (u,v).
– w(T')  w(T), since w(u,v)  w(x,y) T' is
an MST.
– A  T', since A  T and (x,y)A 
A(u,v)  T'
– Thus (u,v) is safe for A.
p
08 Greedy Algorithms.ppt,p-83

18. Assignment 1
 Problems 23.1-1 23.1-7, 23.1-10 Page 566
567
 Last Date
 Tuesday -22 June 2010
Dr. Hanif Durad 18

19. Greedy Algorithms
 Different greedy rules can be used to select the
next vertex to add to the MST being built
1. Krushkal’s Algorithm
2. Prim’s Algorithm
Dr. Hanif Durad 19
SL13.pdf, p-7

20. Two algorithms to find an MST
There are two ways of adding a safe edge:
1. Kruskal’s algorithm: the set A is a forest and
the safe edge added is always the least-weight
edge in the graph connecting two distinct
components.
2. Prim’s algorithm: the set A is a tree and the
safe edge added is always the least-weight edge
connecting A to a vertex not in A
Dr. Hanif Durad 20
lect13.ppt

21. Kruskal’s algorithm
MST-Kruskal(G)
A  
for each vertex vV do
Make-Set(v)
sort the edges in E in non-decreasing weight order
for each edge e = (u,v)E do
if Find-Set(u) ≠ Find-Set(v) /* the trees are distinct */
then
A  A  {e}
Union(u,v) /* combine two trees */
return A 21
lect13.ppt

22. Example: Kruskal’s algorithm
Dr. Hanif Durad 22
b c d
h g f
ia e
8 7
1 2
11 14
4
8
7 6
2
4
9
10
XX
Cost: 37
X

23. Analysis of Kruskal’s algorithm
Dr. Hanif Durad 23
Correctness: follows directly from Theorem 23.1.
Complexity: Depends on the implementation of the set
operations! A naïve implementation takes O(|V| |E|).
 Sorting the edges takes O(|E| lg |E|).
 the for loop goes over every edge and performs two
Find-Set and one Union operation. These can be
implemented to take O(1) amortized time.
The total running time is O(|E| lg |E|) = O(|E| lg |V|)

24. Prim’s algorithm
MST-Prim(G, root)
for each vertex vV do
key(v)  ∞; π[v]  null
key(root)  0; Q  V
while Q is not empty do
u  Extract-Min(Q)
for each v that is a neighbor of u do
if vQ and w(u,v) < key(v)
then π[v]  u
key(v)  w(u,v) /*decrease value of key */
Note: A = {(v, [v]) : v  v - {r} - Q}.
21-greedy.ppt

25. Example: Prim’s algorithm
Dr. Hanif Durad 25
b c d
h g f
ia e
8 7
1 2
11 14
4
8
7 6
2
4
9
10
Cost: 37
∞0
∞ ∞ ∞
∞
∞∞∞

26. Analysis of Prim’s algorithm
Correctness: follows directly from the Theorem 1.
Complexity: Depends on the implementation of the
minimum priority queue. With a binary mean-heap, we
have:
 Building the initial heap takes O(|V|).
 Extract-Min takes O(lg |V|) per vertex  total O(|V| lg |V|)
 The for loop is executed O(|E|).
 Membership test is O(1). Decreasing a key is O(lg |V|).
Overall, the running time is O(|V| lg |V| + |E| lg |V|) = O(|E|
lg |V|).
Dr. Hanif Durad 26

27. Assignment 2
 Section Problems 23.2-1 23.2-5, 23.2-8 Page
574 574
 Chapter Problems 23-1, 23-323-4
 C++ coding for Kruskal’s and Prim’s
Algorithms
 Last Date
 Tuesday -22 June 2010
Dr. Hanif Durad 27