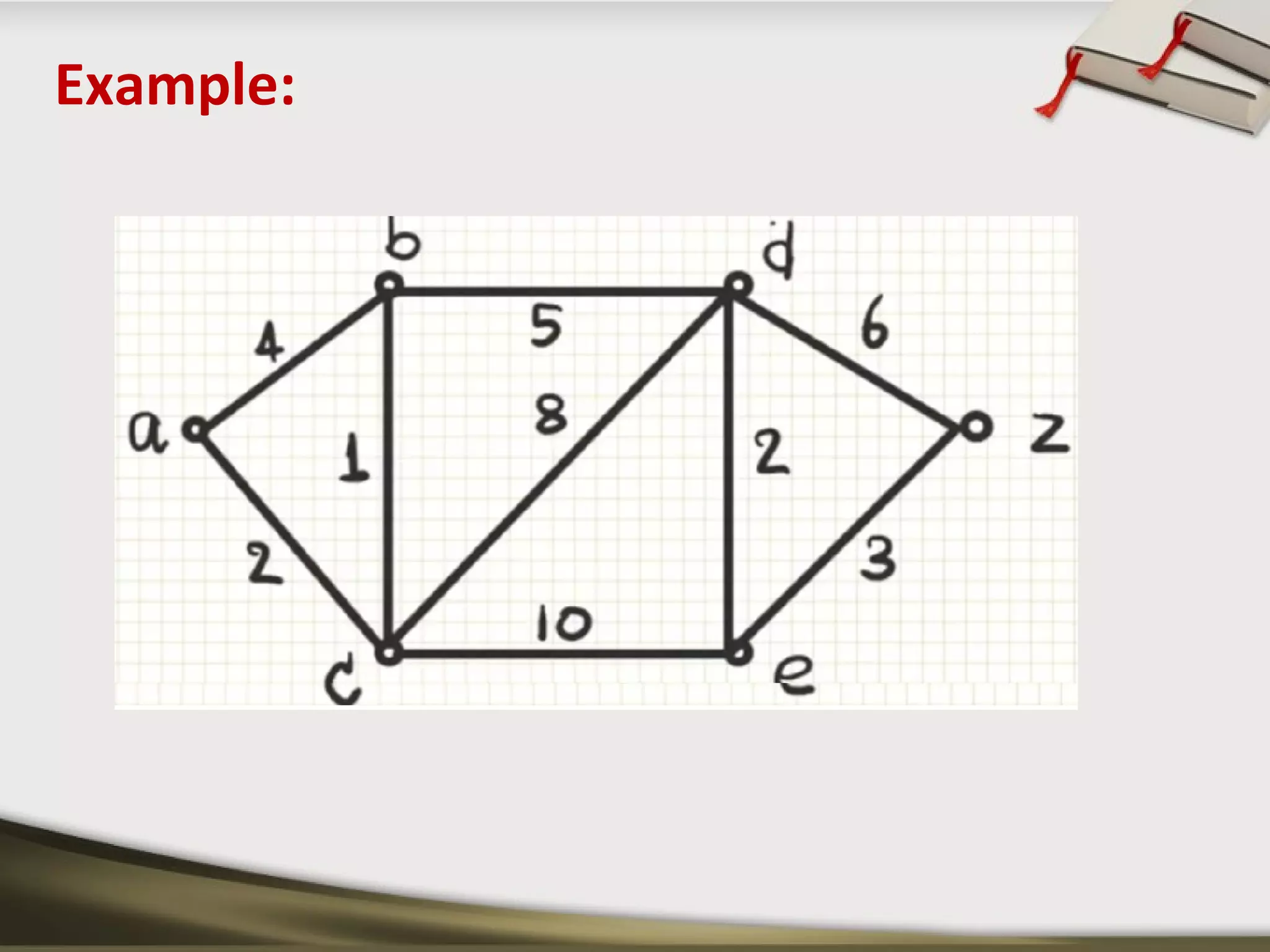
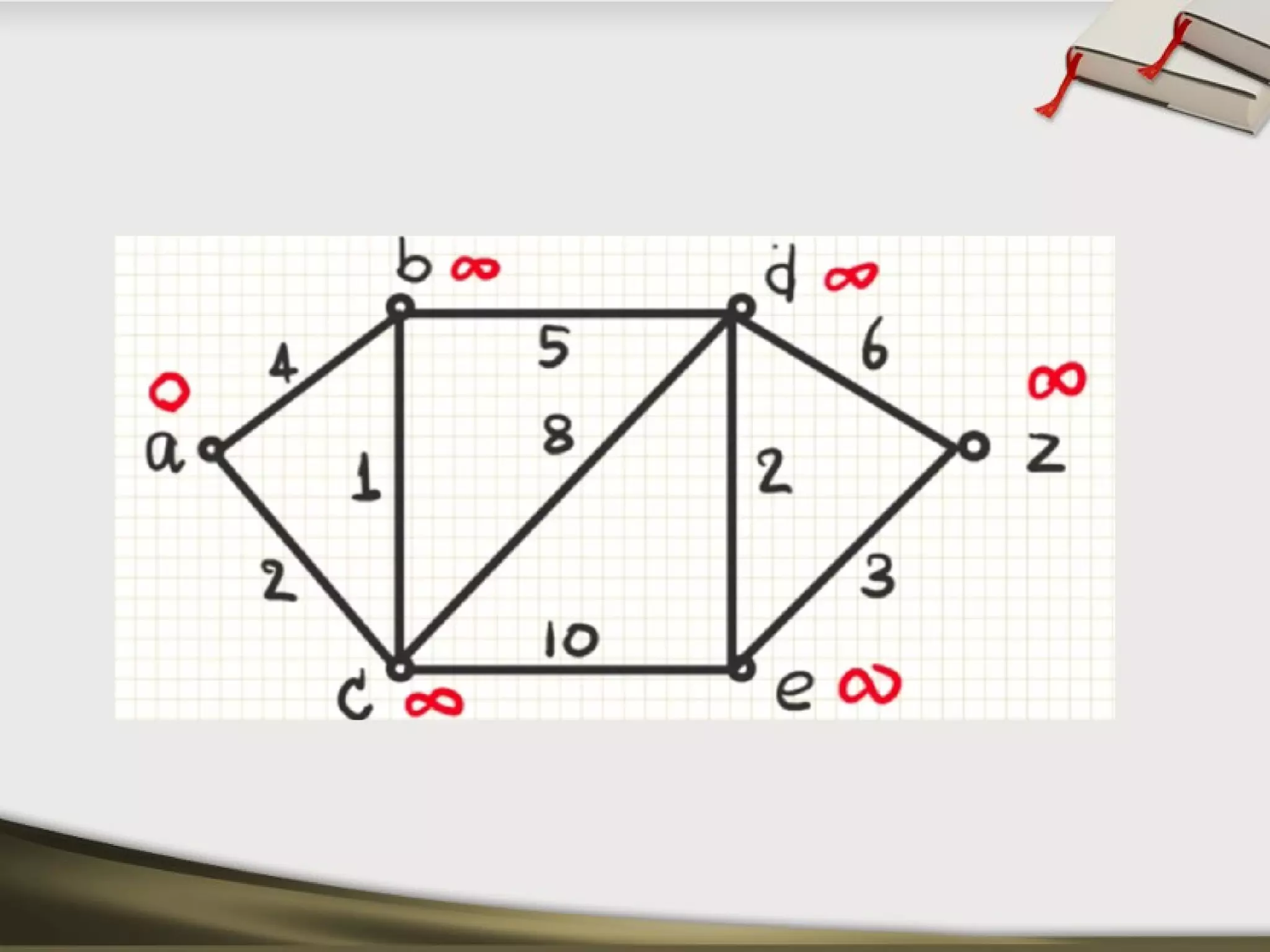
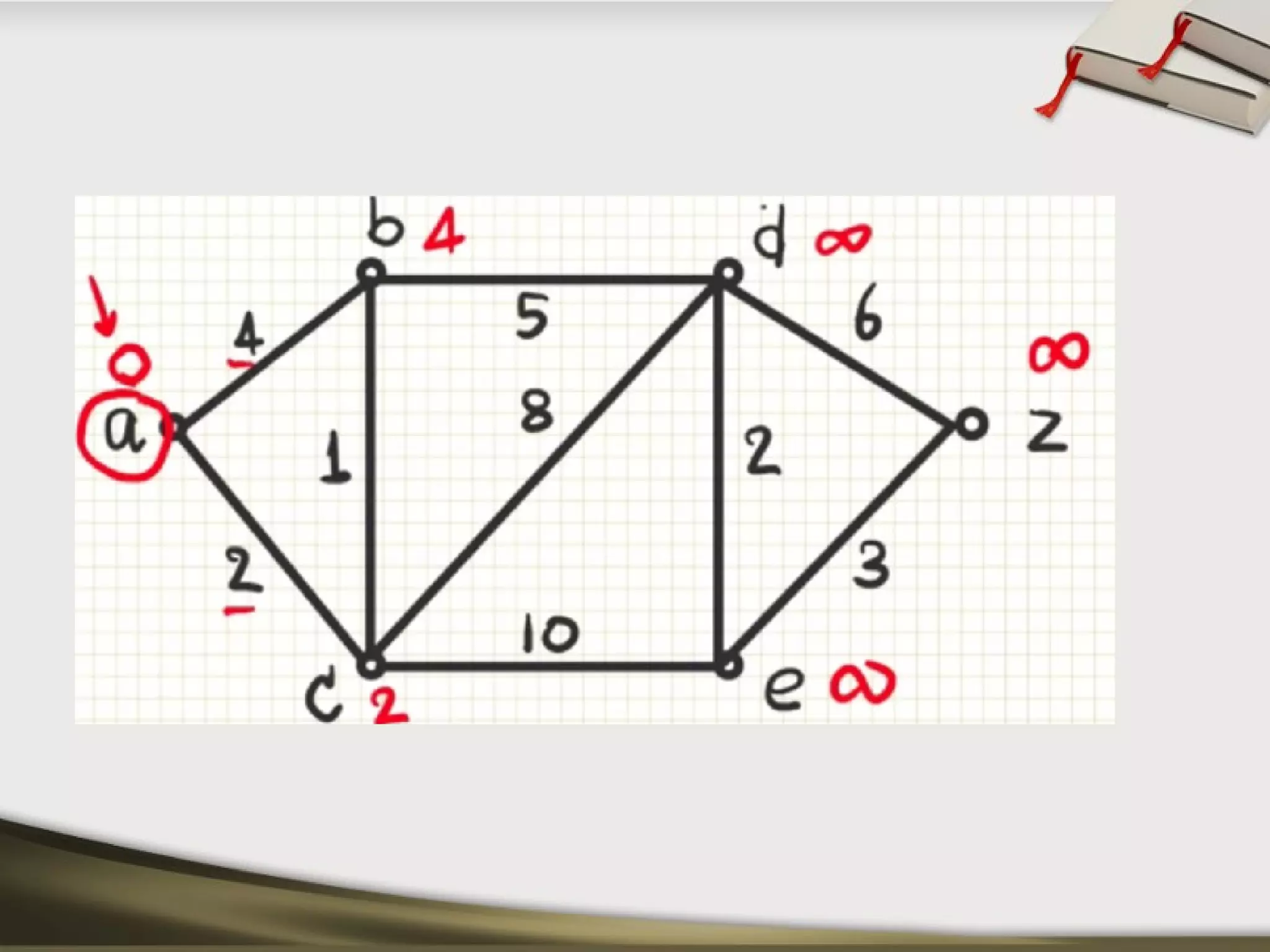
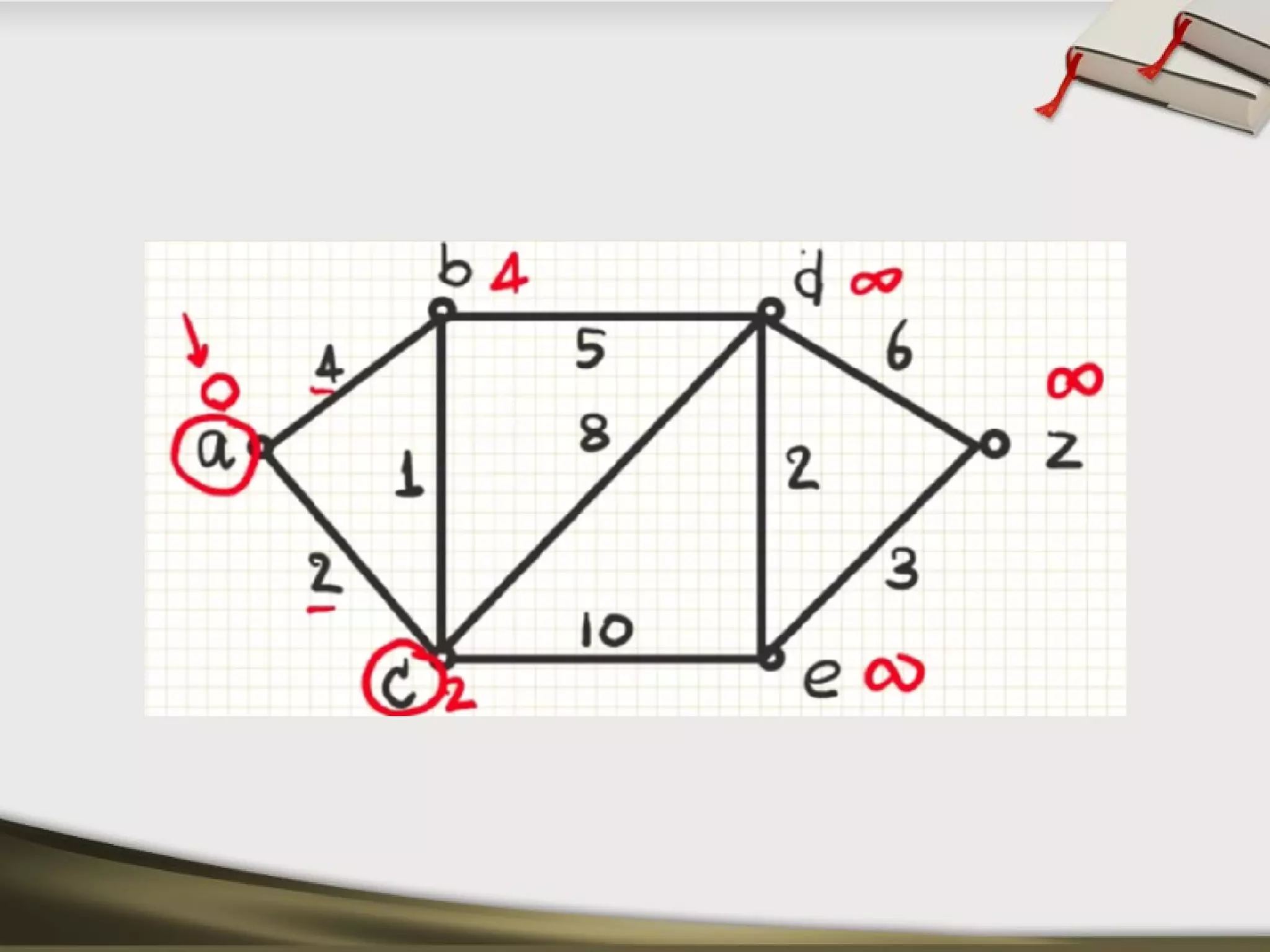
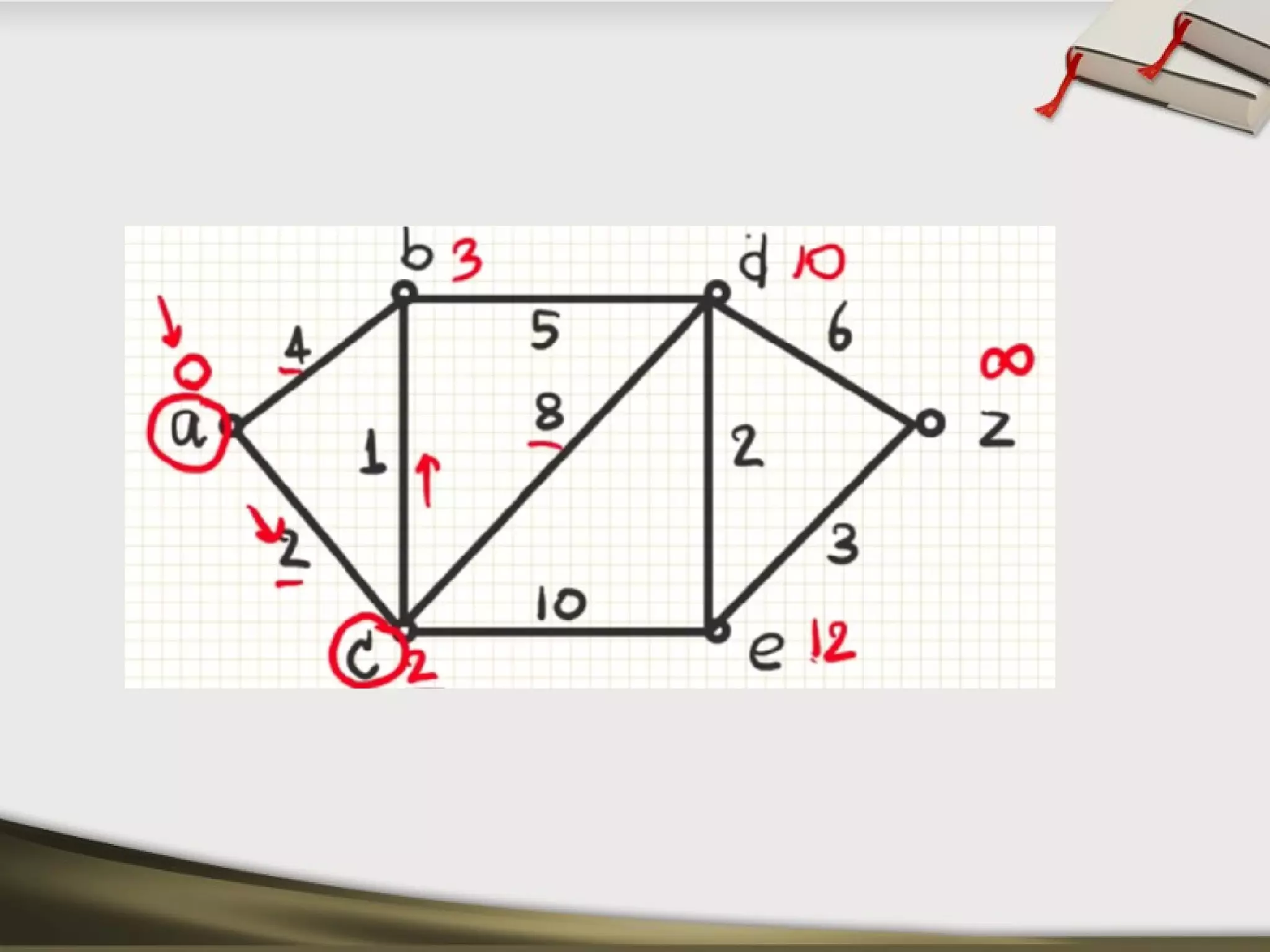
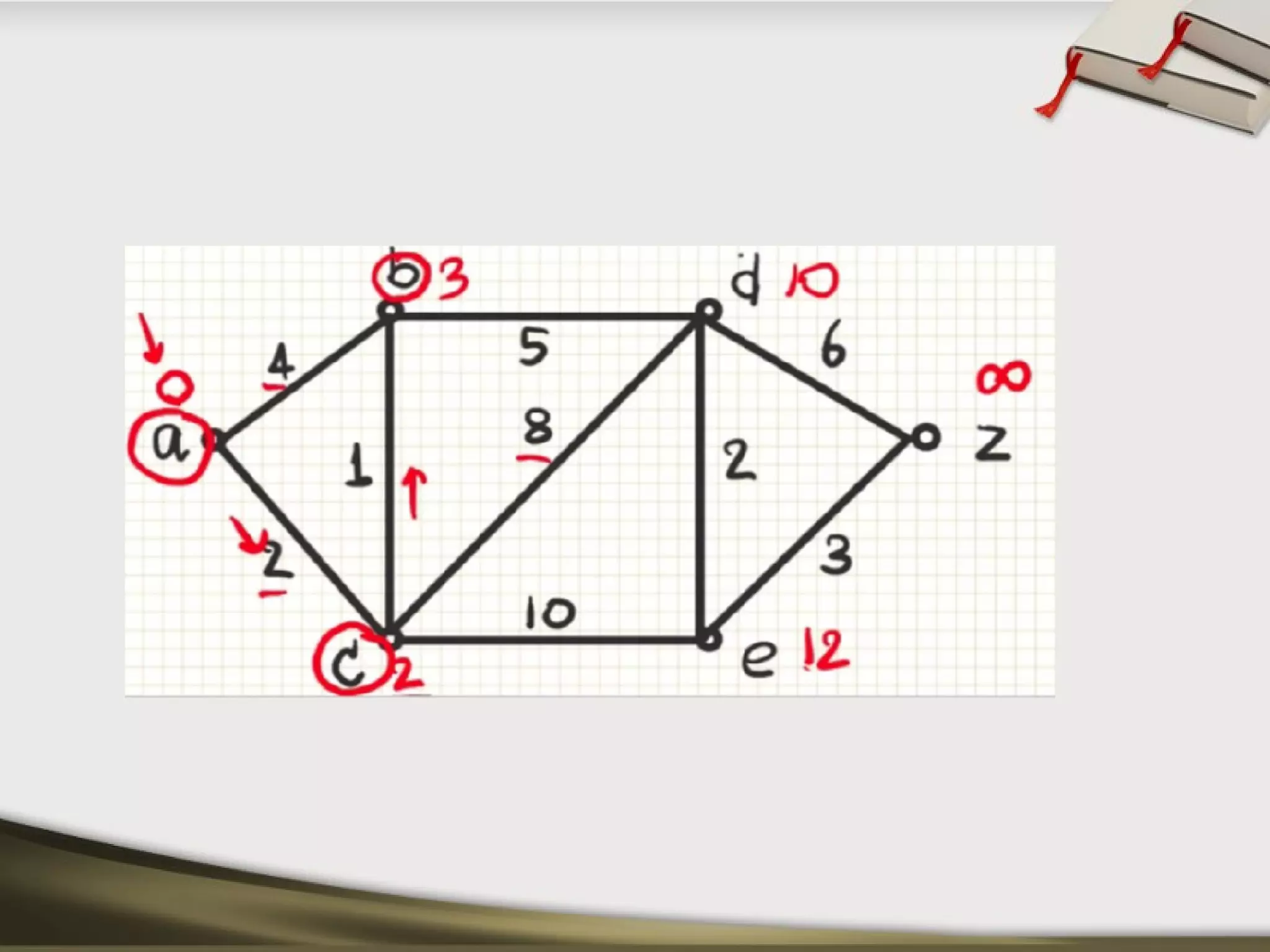
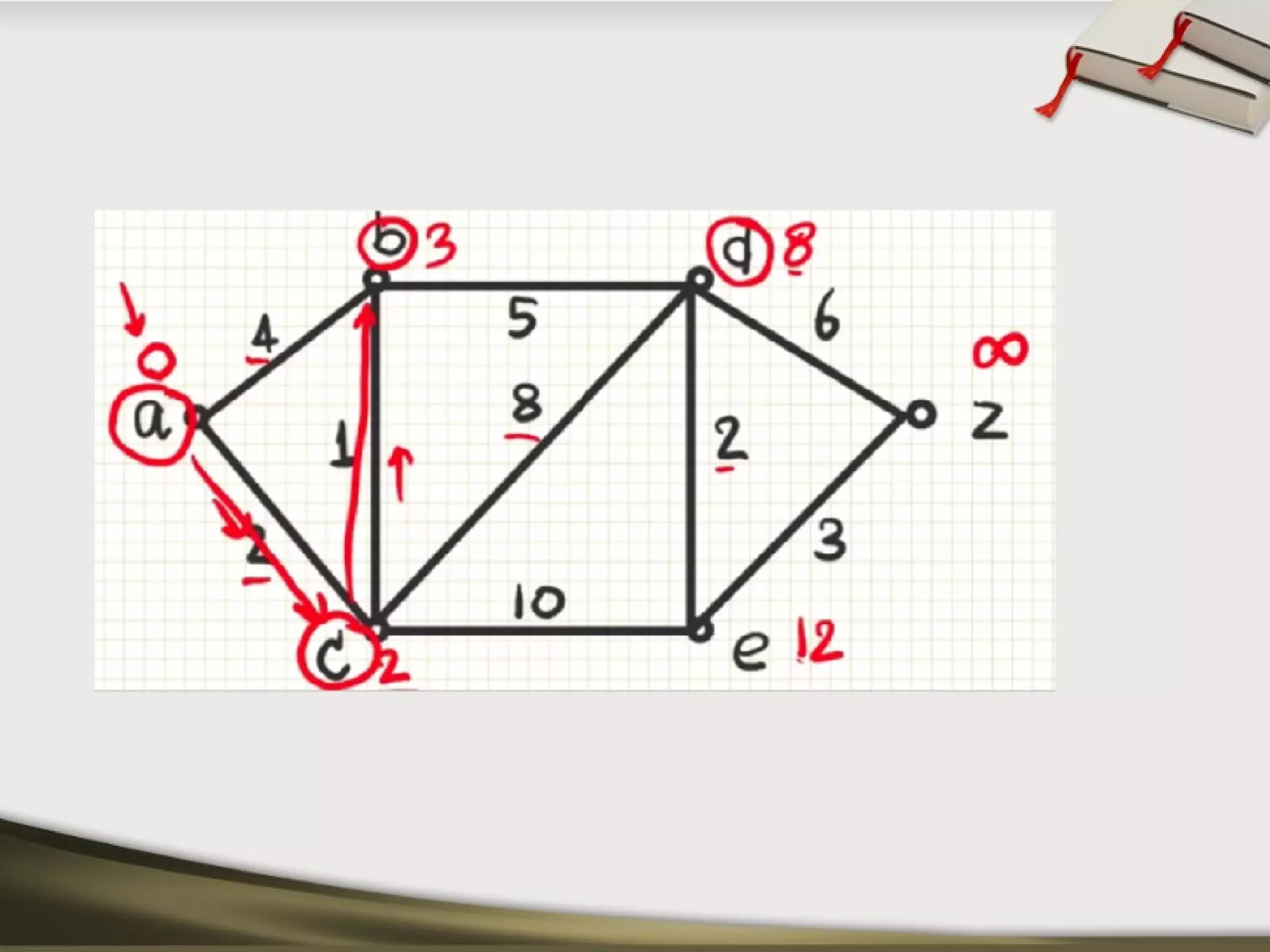
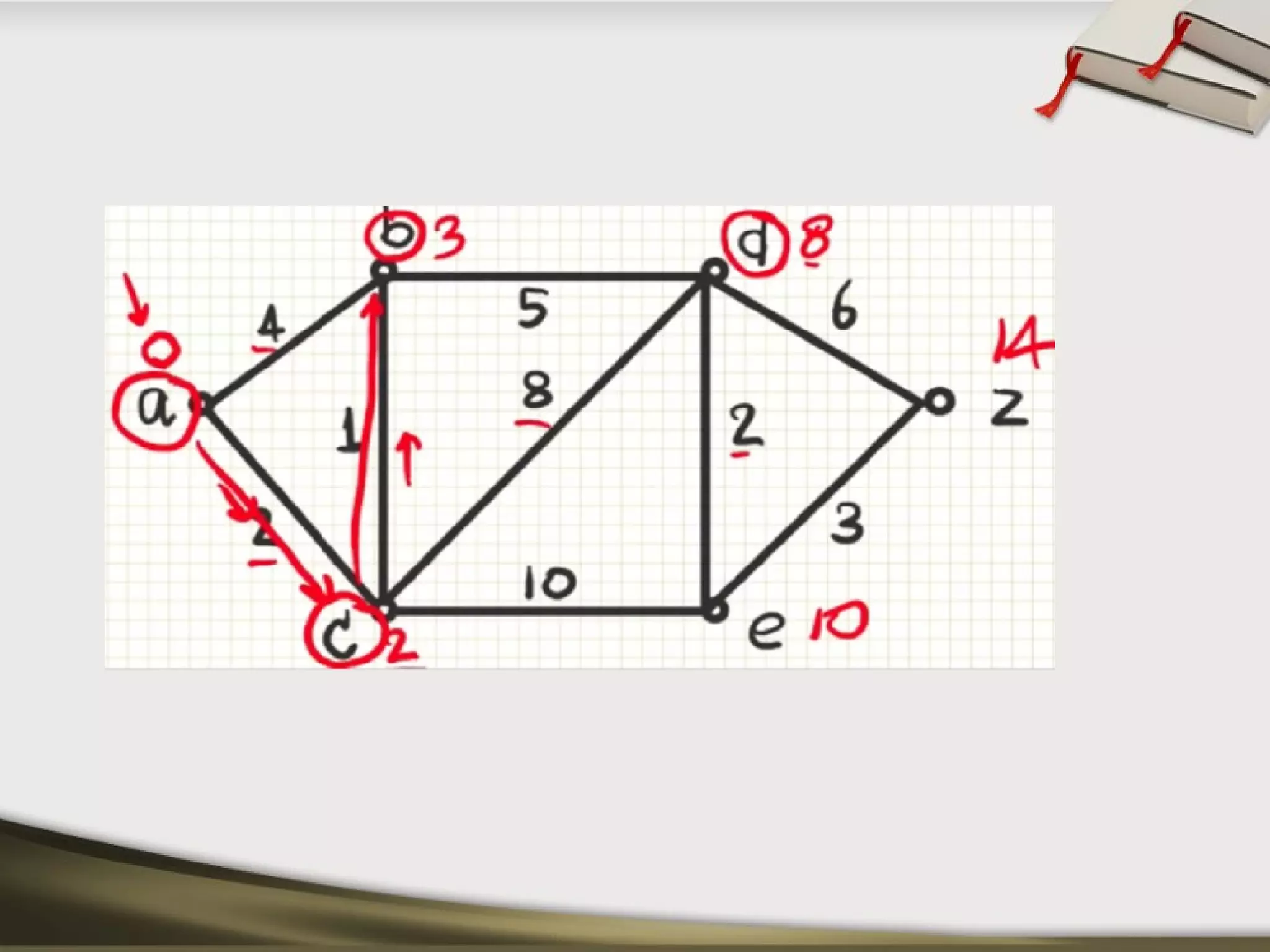
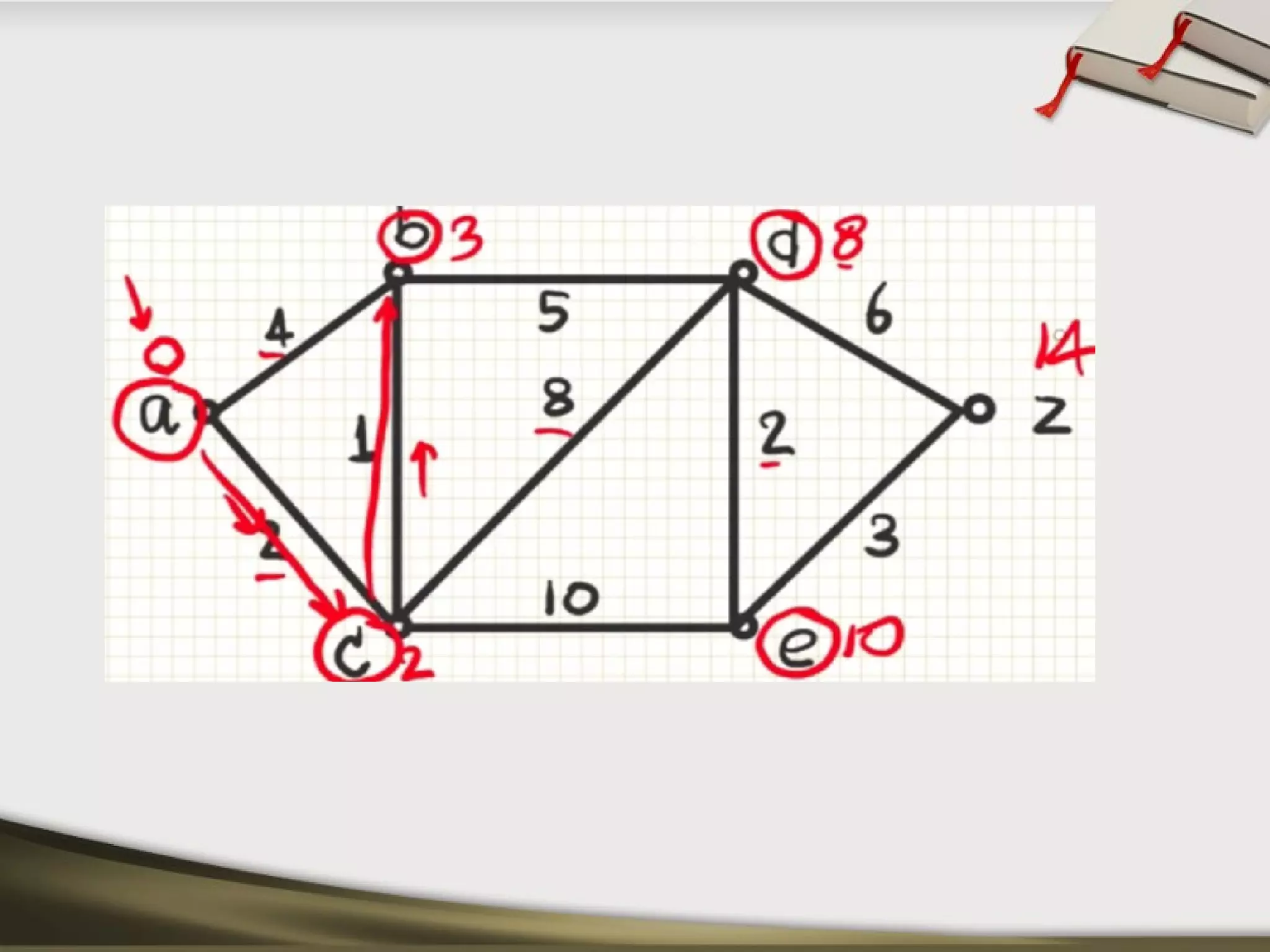
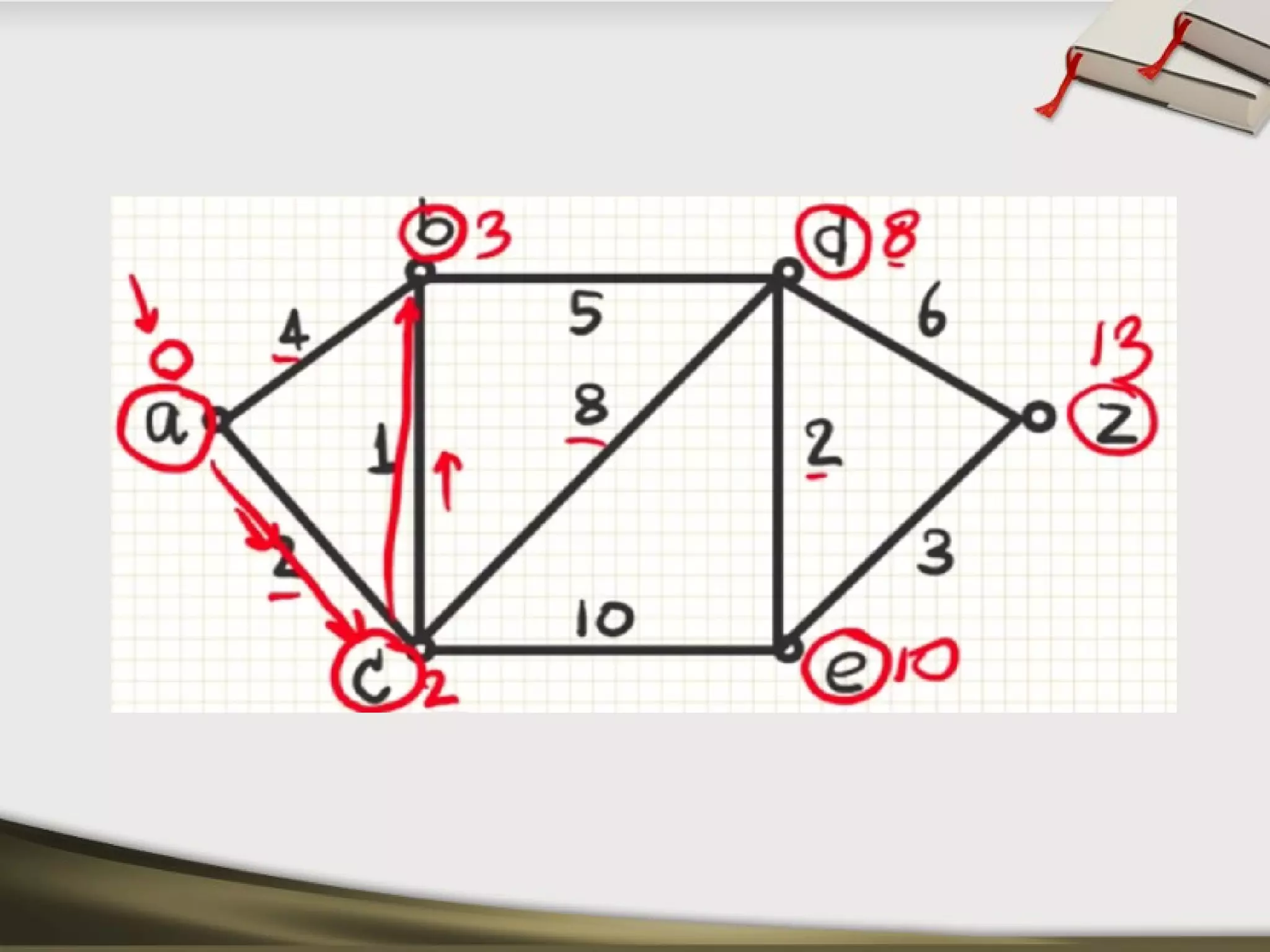
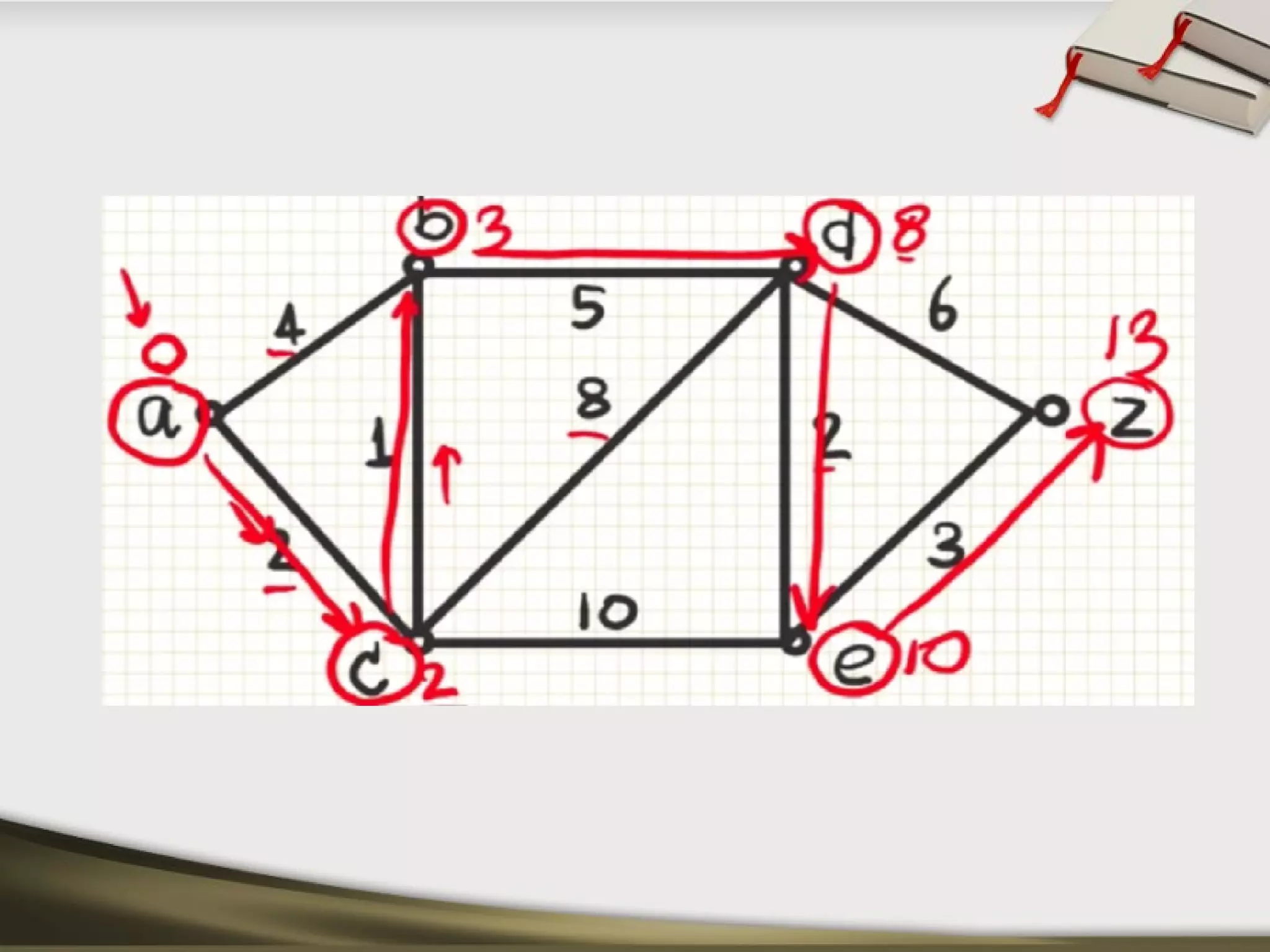
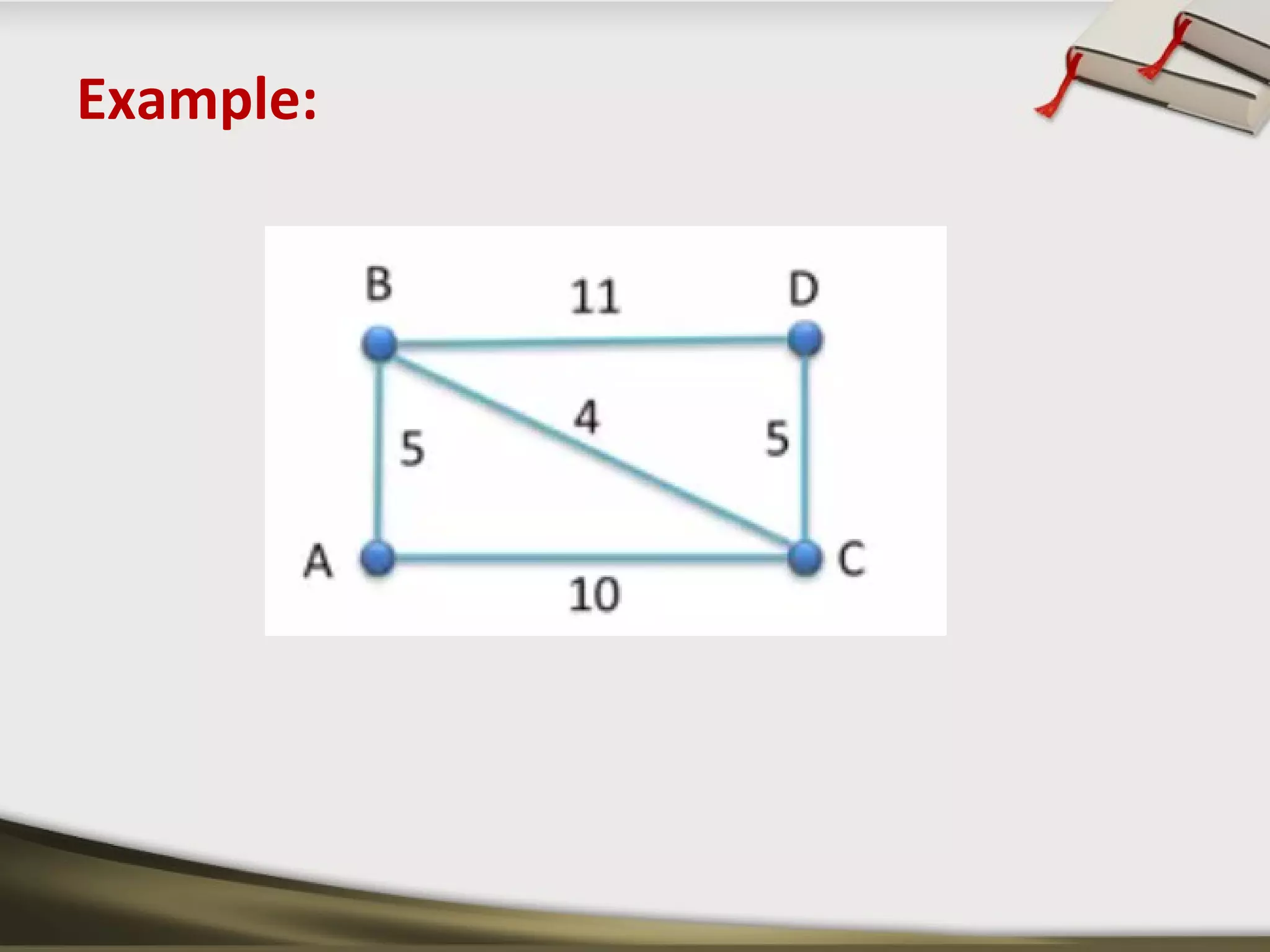
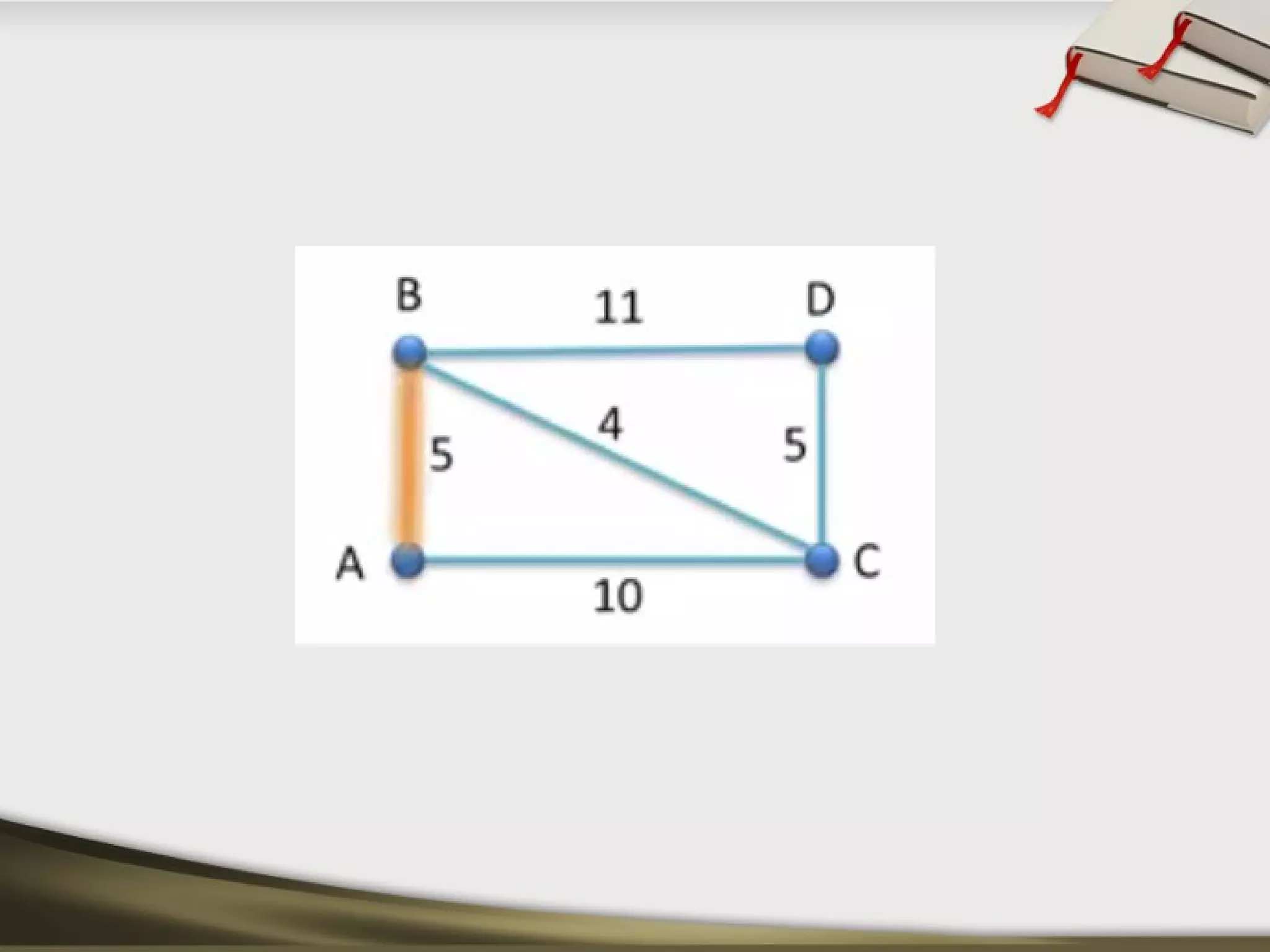
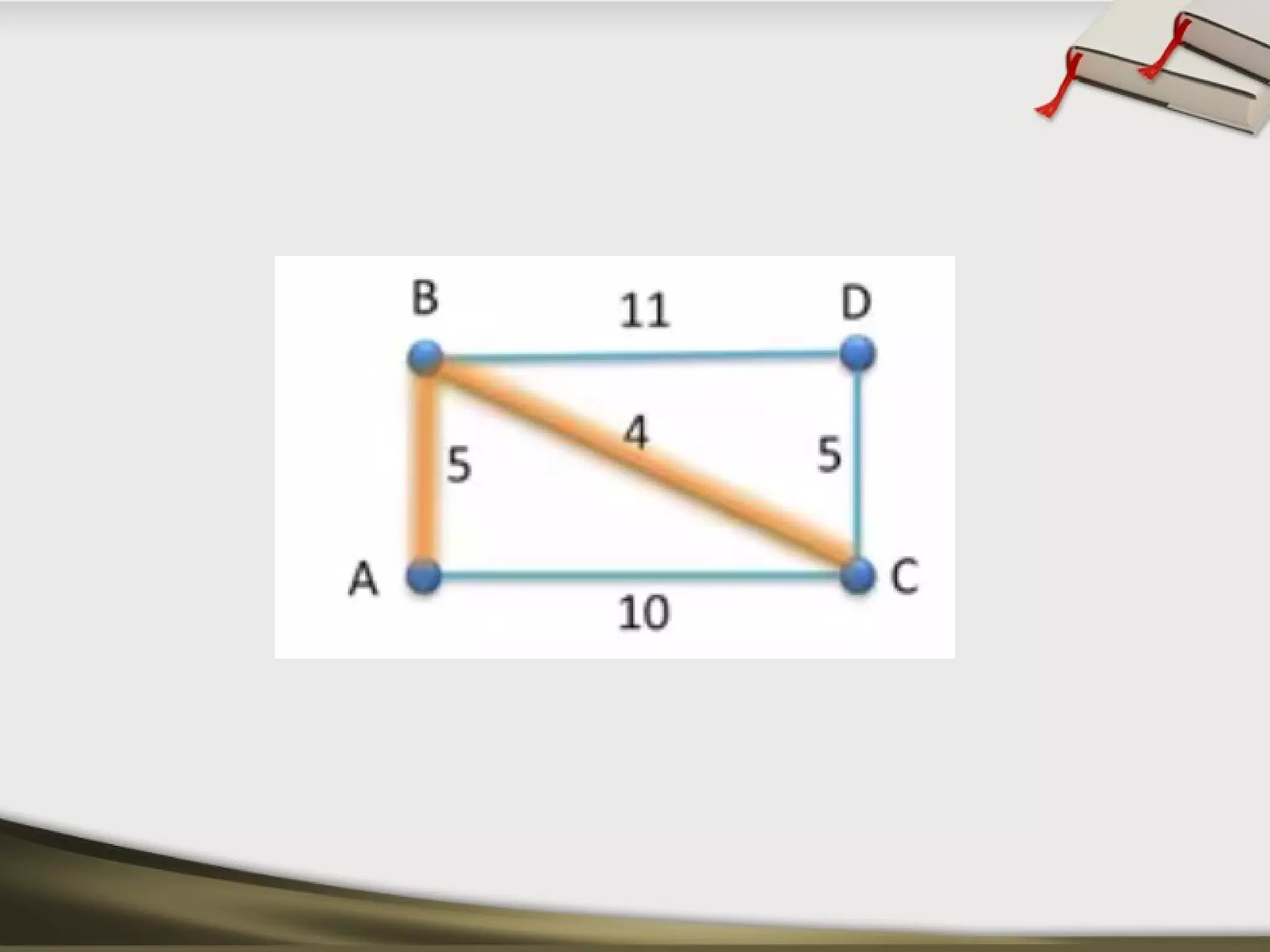
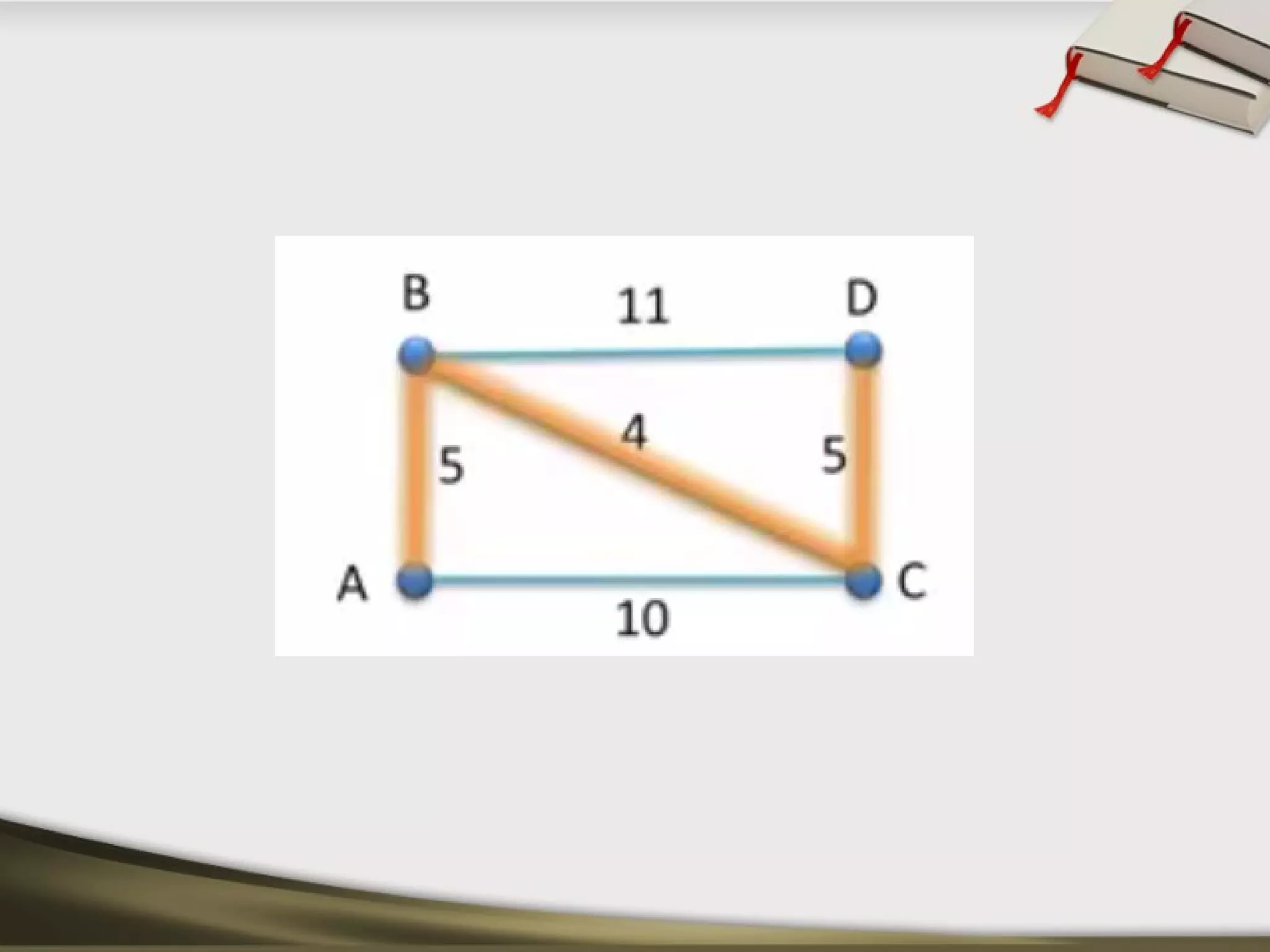
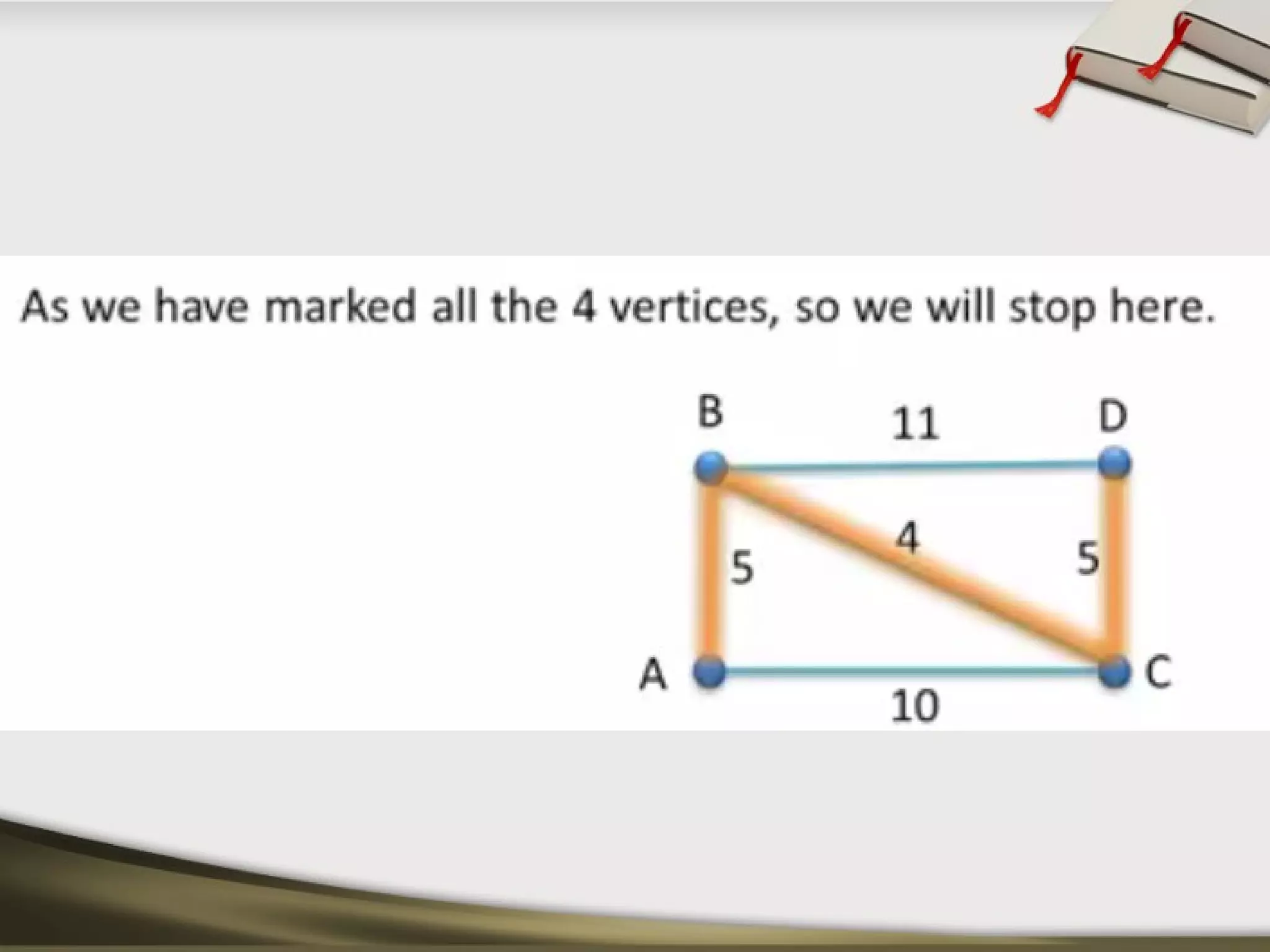
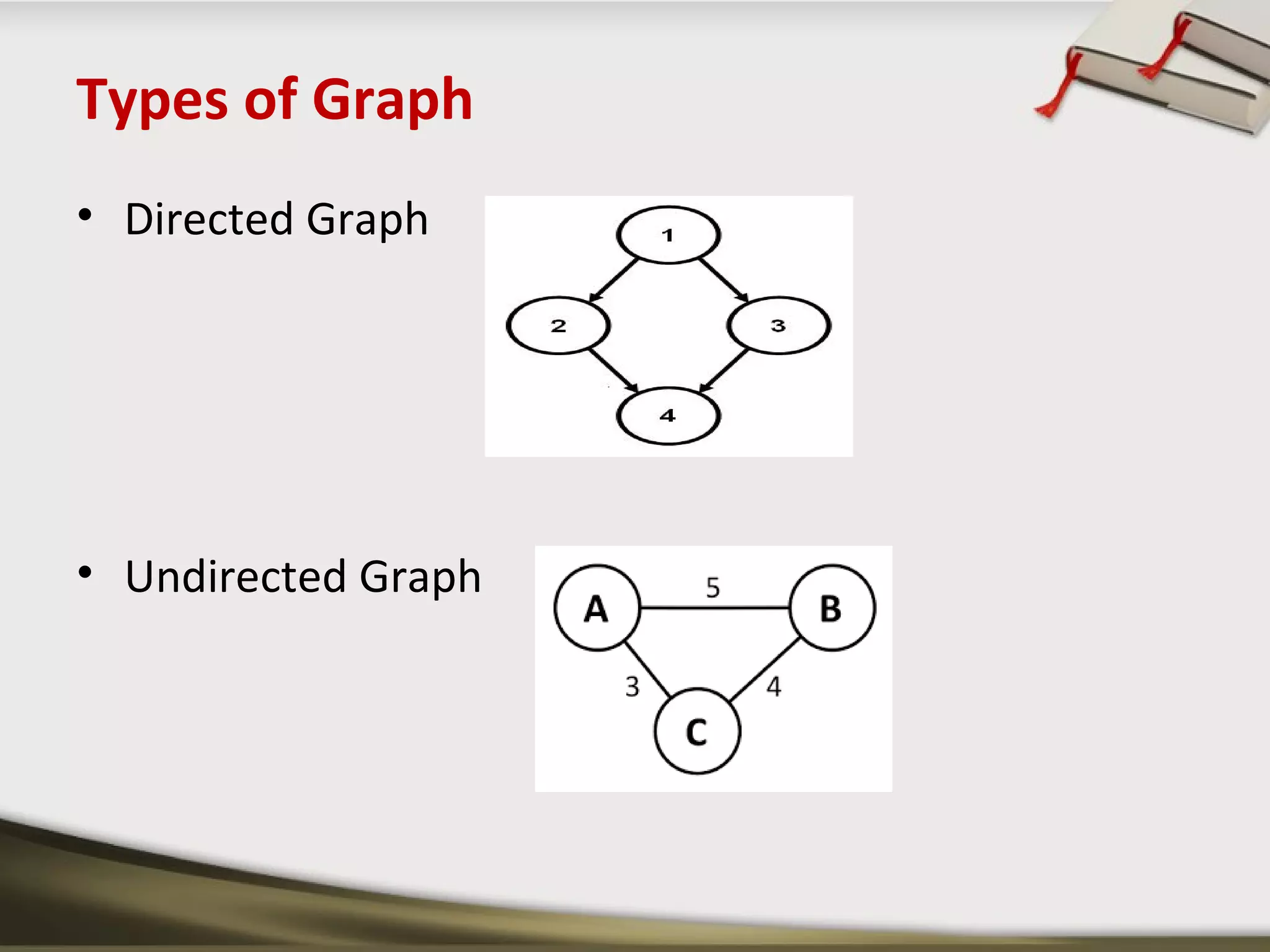
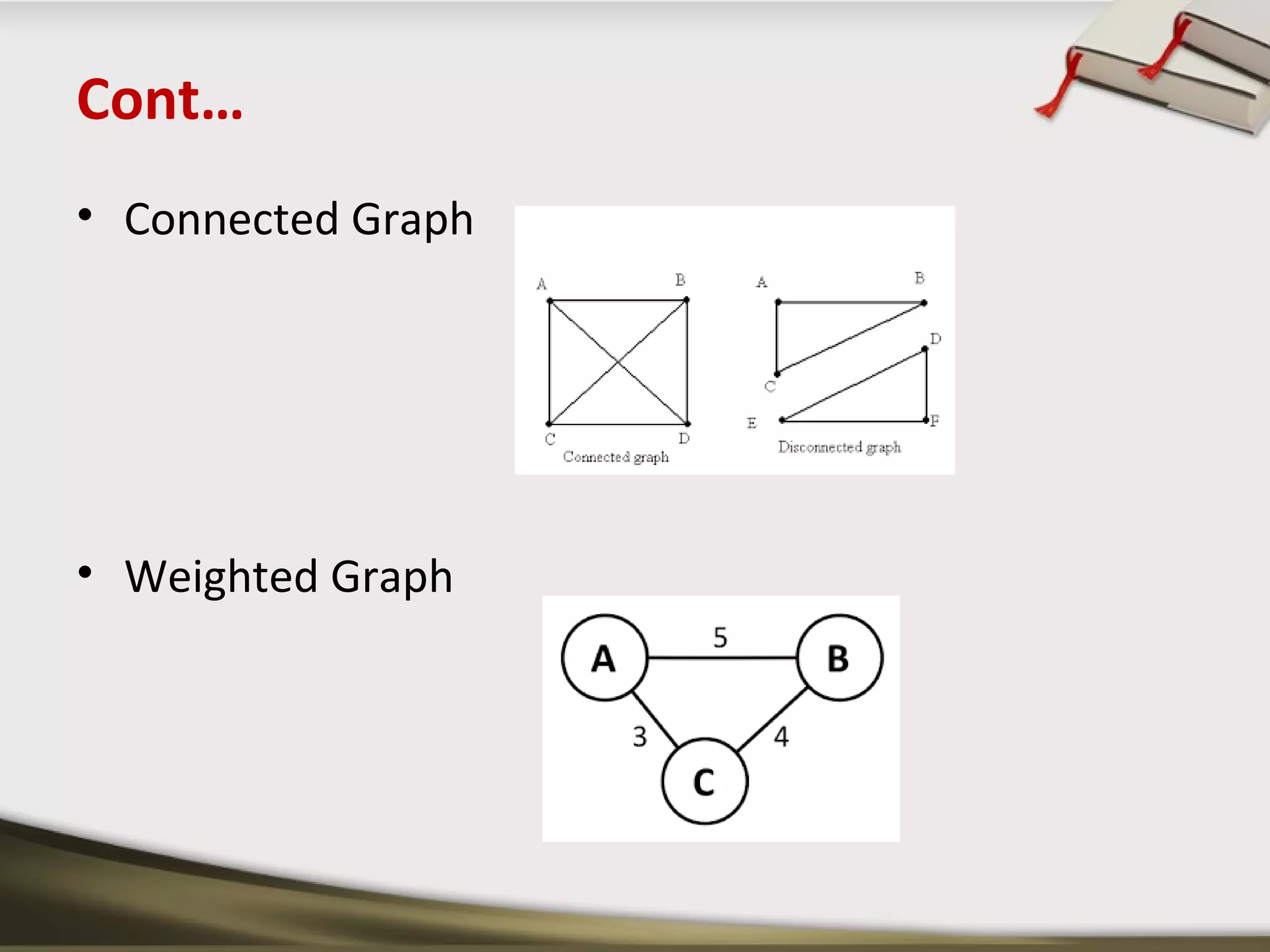
The document discusses shortest path problems and algorithms for finding shortest paths in graphs. It describes Dijkstra's algorithm for finding the shortest path between two nodes in a graph with non-negative edge weights. Prim's algorithm is presented for finding a minimum spanning tree, which is a subgraph connecting all nodes with minimum total edge weight. An example graph is given and steps are outlined for applying Prim's algorithm to find its minimum spanning tree.

1. SHORTEST PATH PROBLEM
Submitted to: Submitted by:
Mrs. Priyanka Soni Krati Katyal
MCA 2nd
Sem

2. Topic Covered
• GRAPH
• SHORTEST PATH PROBLEM
• DIJKISTRA’S ALGORITHM
• EXAMPLE
• SPANNING TREE
• PRIM’S ALGORITHM
• EXAMPLE

3. Graph
• A graph is a structure consisting of a set of arrays
(also called dimensions) and a set of edges .
• An edge is a pair of vertices and the two vertices are
called the edge endpoints.
• It is represented as G(V,E).
• Edges(n(n-1)/2)
• Vertices(n)

4. Types of Graph
• Directed Graph
• Undirected Graph

5. Cont…
• Connected Graph
• Weighted Graph

6. • In graph theory, the degree (or valency ) of a vertex of
a graph is the number of edges incident to the vertex,
with loops counted twice.
• The degree of a vertex is denoted or . The maximum
degree of a graph G, denoted by Δ(G), and the minimum
degree of a graph, denoted by δ(G).
• In a regular graph, all degrees are the same, and so we
can speak of the degree of the graph.
Degree

7. • the number of head endpoints adjacent to a node is
called the indegree of the node and the number of
tail endpoints adjacent to a node is its outdegree.
• The indegree is denoted as deg-(v) and the
outdegree as deg+(v).
Indegree and Outdegree

8. Shortest Path Problem
• If all the edges in a graph have non-negative weights,
then it is possible to find the shortest path from any
two vertices.
• For example, lets assume in a figure, the shortest
path from B to F is { B, A, C, E, F } with a total cost of
nine.
• Thus, the problem is well defined for a graph that
contains non-negative weights.

9. • In an weighted graph, the weight of an edge measures
the cost of traveling that edge.
• For example, in a graph representing a network of
airports, the weights could represent: distance, cost or
time.
• Such a graph could be used to answer any of the
following:
– What is the fastest way to get from A to B?
– Which route from A to B is the least expensive?
– What is the shortest possible distance from A to B?
Shortest Path Problem

10. Dijkistra’s Algorithm
function Dijkstra(Graph, source):
dist[source] ← 0
prev[source] ← undefined
for each vertex v in Graph:
if v ≠ source
dist[v] ← infinity
prev[v] ← undefined
end if
add v to Q
end for

11. while Q is not empty:
u ← vertex in Q with min dist[u]
remove u from Q
for each neighbor v of u:
alt ← dist[u] + length(u, v)
if alt < dist[v]
dist[v] ← alt
prev[v] ← u
end if
end for
end while
Cont…

12. return dist[], prev[]
end function

13. Example:

24. 1.Given a road map of Europe find the distance from
Wien to all other capitals on the map. - Represent cities
as vertices, roads as edges and distances between
cities as edge weights. Then, find the shortest paths to
all vertices the vertex that represents Wien.
2. Given the schedule of all airline flights and their
flying-times what is the fastest way to go from Wien to
Calcutta.
3. Urban traffic planning.
4. Routing of telecommunications messages.
Application

25. Spanning Tree
In the mathematical field of graph theory, a spanning
tree T of an undirected graph G is a sub graph that
includes all the vertices of G that is a tree.
In general, a graph may have several spanning trees,
but a graph that is not connected will not contain a
spanning tree .
Algorithm :
 Prim’s Algorithm
 Kruskal Algorithm

26. Prim’s Algorithm
Initially discovered in 1930 by Vojtěch Jarník, then
rediscovered in 1957 by Robert C. Prim
Prim's algorithm is a greedy algorithm that finds
a minimum spanning tree for a connected weighted
undirected graph.
This means it finds a subset of the edges that forms
a tree that includes every vertex, where the total weight of
all the edges in the tree is minimized.

27. A graph can have one or more number of spanning trees.
If the graph has N vertices then the spanning tree will have
n-1 edges
A minimum spanning tree is a spanning tree that has the
minimum weight than all other spanning trees of the
graph.
cont...

28. Prim’s Algorithm
Step 0: Pick any vertex as a starting vertex. (Call
it A). Mark it with any given color, say orange.
Step 1: Find the nearest neighbor of A (call it B).
Mark both vertex and the edge AB orange.
Step 2: Find the nearest uncolored neighbor to
the orange sub graph (i.e., the closest vertex to
any red vertex). Mark it and the edge connecting
the vertex to the red sub graph in orange.
Step 3: Repeat Step 2 until all vertices are marked
orange. The orange sub graph is a minimum
spanning tree.

29. Example:

35. Reference
•www.google.com
•www.wikipidea.com
•H. coreman

36. MLSU UNIVERSITY