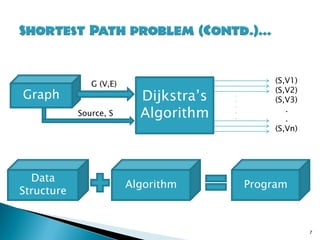
This document describes Floyd's algorithm for solving the all-pairs shortest path problem in graphs. It begins with an introduction and problem statement. It then describes Dijkstra's algorithm as a greedy method for finding single-source shortest paths. It discusses graph representations and traversal methods. Finally, it provides pseudocode and analysis for Floyd's dynamic programming algorithm, which finds shortest paths between all pairs of vertices in O(n3) time.

1. S.SRIKRISHNAN
II year
CSE Department
SSNCE
1
The shortest distance between two points is under construction. – Noelie Altito
FLOYD’ ALGORITHM DESIGN

2.  Introduction
 Problem statement
 Solution
◦ Greedy Method (Dijkstra’s Algorithm)
◦ Dynamic Programming Method
 Applications
2

3.  A non-linear data structure
 Set of vertices and edges
 Classification
◦ Undirected graph
◦ Directed graph (digraph)
 Basic terminologies
◦ Path
◦ Cycle
◦ Degree
3

4.  Representation
◦ Incidence Matrix
◦ Adjacency Matrix
◦ Adjacency List
◦ Path Matrix
 Traversals
◦ Depth first (Stack ADT)
◦ Breadth first (Queue ADT)
4

5.  Standard Problems
◦ Travelling salesman problem
◦ Minimum spanning tree problem
◦ Shortest path problem
◦ Chinese postman problem
5

6.  To find the shortest path between source and
other vertices
 Greedy method
 Assumptions
◦ A directed acyclic graph
◦ No negative edges
 Unweighted or weighted Graph
6

7. 7
Graph
Source, S
G (V,E) (S,V1)
(S,V2)
(S,V3)
.
.
(S,Vn)
Algorithm
Data
Structure
Program
Dijkstra’s
Algorithm
.
.
.
.
.

8. 8
Step 1
•Assign to every node a distance value. Set it to zero for our initial
node and to infinity for all other nodes.
Step 2
•Mark all nodes as unvisited. Set initial node as current.
Step 3
•For current node, consider all its unvisited neighbours and calculate
their distance (from the initial node).
Step 4
•If this distance is less than the previously recorded distance (infinity
in the beginning, zero for the initial node), overwrite the distance.

9. 9
Step 5
•When we are done considering all neighbours of the current node,
mark it as visited.
Step 6
•A visited node will not be checked ever again; its distance recorded
now is final and minimal.
Step 7
•Set the unvisited node with the smallest distance (from the initial
node) as the next "current node" and continue from step 3
Step 8
•Stop

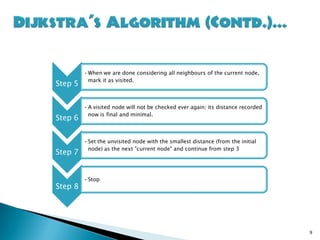
10. Pseudo code
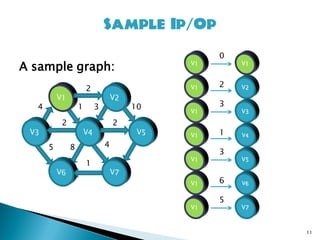
1. function Dijkstra (Graph, source):
2. for each vertex v in Graph: // Initializations
3. dist[v] := infinity // Unknown distance function from source to v
4. previous[v] := undefined // Previous node in optimal path from source
5. dist[source] := 0 // Distance from source to
source
6. Q := the set of all nodes in Graph // All nodes in the graph are unoptimized -
thus are in Q
7. while Q is not empty: // The main loop
8. u := vertex in Q with smallest dist[]
9. if dist[u] = infinity:
10. break // all remaining vertices are inaccessible from source
11. remove u from Q
12. for each neighbor v of u: // where v has not yet been removed from Q
13. alt := dist[u] + dist_between(u, v)
14. if alt < dist[v]: // Relax (u,v,a)
15. dist[v] := alt
16. previous[v] := u
17. return dist[]
Running time: O((n+|E|)log n)
10

11. A sample graph:
2
4
103
2
2
4 1
1
85
0
2
3
1
3
6
5
Sample Ip/Op
11

12. Result and Scope of DA
 The shortest path between a source vertex to
all other vertices have been found
 Problem statement could me modified to:
◦ To find shortest path between all vertices to a
particular vertex (destination)
◦ How do I change the algorithm ?
12

13. Problem Extensions
 The SINGLE-SOURCE SHORTEST PATH PROBLEM, in which
we have to find shortest paths from a source vertex v to
all other vertices in the graph.
 The SINGLE-DESTINATION SHORTEST PATH PROBLEM, in
which we have to find shortest paths from all vertices in
the graph to a single destination vertex v. This can be
reduced to the single-source shortest path problem by
reversing the edges in the graph.
 The ALL-PAIRS SHORTEST PATH PROBLEM, in which we
have to find shortest paths between every pair of
vertices v, v' in the graph.
13

14. Graph
Source, S
G (V,E)
Dijkstra’s
Algorithm
.
.
.
.
.
(S,V1)
(S,V2)
(S,V3)
.
.
(S,Vn)
(-)
Graph
Destination, D
G (V,E)
Dijkstra’s
Algorithm
.
.
.
.
.
(D,V1)
(D,V2)
(D,V3)
.
.
(D,Vn)
SINGLE-SOURCE SHORTEST PATH PROBLEM
SINGLE-DESTINATION SHORTEST PATH PROBLEM
Graph
G (V,E)
Dijkstra’s
Algorithm
.
.
.
.
.
(V1,V1)
(V1,V2)
(V1,V3)
.
.
(Vn,Vn)
ALL - PAIRS SHORTEST PATH PROBLEM
14

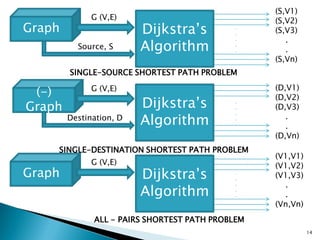
15. All Pairs Shortest Path problem
 The all-pairs shortest path algorithm is to determine
a matrix A such that A(i, j) is the length of the
shortest path between i and j.
 Input given as a matrix form
 Output is an nXn matrix D = [dij] where dij is the
shortest path from vertex i to j.
Wij =
0, if i=j
W(i, j), if (i,j) ε E
∞, if (i,j) ε E
15

16. Solution 1
 If there are no negative cost edges apply
Dijkstra’s algorithm to each vertex (as the
source) of the digraph.
 Disadvantage
 Running time increases to O(n(n+|E|)log n)
 Therefore we go for Dynamic Programming
16

17. 17
Dynamic Programming
 An algorithm design method that can be used
when the solution to the problem can be viewed
as a result of a sequence of decisions.
 Best examples:
 Ordering matrix multiplication
 Optimal binary search trees
 All pairs-shortest path

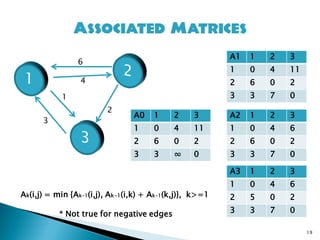
18. 18
Solution 2
 To find the shortest path from i to j (i!=j)
 Assume some intermediate vertex k (or no
vertices also)
 The shortest path from i to j is the shortest
path from [(i,k) + (k,j) or i to j ] which ever is
shorter.
 We use associated matrices and its powers to
calculate the shortest path from i to k and also
k to j.
 Matrix obtained in O(n.n.n)

19. 19
Associated Matrices
1
6
3
4
2
A0 1 2 3
1 0 4 11
2 6 0 2
3 3 ∞ 0
A1 1 2 3
1 0 4 11
2 6 0 2
3 3 7 0
A2 1 2 3
1 0 4 6
2 6 0 2
3 3 7 0
A3 1 2 3
1 0 4 6
2 5 0 2
3 3 7 0
Ak(i,j) = min {Ak-1(i,j), Ak-1(i,k) + Ak-1(k,j)}, k>=1
* Not true for negative edges

20. 20
Pseudo Code
1. algorithm allpairs (cost, A, n):
2. //cost[1:n, 1:n] is the cost adjacency matrix of a graph with n
vertices
3. //A[i,j] is the cost of a shortest path from vertex i toj .
4. //cost[i,i] = 0 for 1<=i<=n.
5. {
6. for(i=0;i<n;i++)
7. for(j=0;j<n;j++)
8. A[i][j]=cost[i][j] //copy cost into A
9. for(k=0;k<n;k++)
10. for(i=0;i<n;i++)
11. for(j=0;j<n;j++)
12. A[i,j] = min { A[i,j] , A[i,k] + A[k,j] };
13. }

21. 21
Applications
 To automatically find directions between
physical locations
 Vehicle Routing and scheduling
 In a networking or telecommunication
applications, Dijkstra’s algorithm has been used
for solving the min-delay path problem (which
is the shortest path problem). For example in
data network routing, the goal is to find
the path for data packets to go through a
switching network with minimal delay.

22. 22
New York To Los Angels 

23. 23
A Real Life Problem
 Whole pineapples are served in a restaurant in London. To
ensure freshness, the pineapples are purchased in Hawaii and air
freighted from Honolulu to Heathrow in London. The following
network diagram outlines the different routes that the
pineapples could take.
105
68
57
76
65
88
105
4875
44
63
56
71

24. 24
References
 Data Structures and Algorithm Analysis in C,
Second Edition, M.A. Weiss
 Fundamentals of Computer Algorithms, Second
Edition, Ellis Horowitz, Sartaj Sahni,
Sanguthevar Rajasekaran
 Introduction to Design and Analysis of
Algorithms, Fifth Edition, Anany Levitin

25. 25