This document provides an outline and overview of topics related to arrays and matrices. It begins with an introduction to one-dimensional arrays, how they are represented in memory, and common operations on arrays. It then discusses the limitations of linear arrays and introduces multidimensional arrays. Specific types of multidimensional arrays covered include two-dimensional arrays and special matrices such as diagonal, tridiagonal, lower triangular, and upper triangular matrices. Memory mapping techniques for multidimensional arrays like row-major and column-major ordering are also summarized.

1. Chapter 3
Arrays and Matrices
Dr. Muhammad Hanif Durad
Department of Computer and Information Sciences
Pakistan Institute Engineering and Applied Sciences
hanif@pieas.edu.pk
Some slides have bee adapted with thanks from some other lectures
available on Internet. It made my life easier, as life is always
miserable at PIEAS (Sir Muhammad Yusaf Kakakhil )

2. Dr. Hanif Durad 2
Lecture Outline (1/2)
 Introduction
 One-Dimensional Arrays
 Representing 1-D arrays in Memory
 Operations on arrays
 Limitations Of Linear Arrays
 Multidimensional Arrays
 Row- and Column-Major Mappings

3. Dr. Hanif Durad 3
Lecture Outline (2/2)
 Special Matrices
 Diagonal:
 Tridiagonal:
 Lower triangular:
 Upper triangular:
 Symmetric
 Strings

4. 3.1 Introduction
 Arrays are most frequently used in programming
 Data is often available in tabular form
 Tabular data is often represented in arrays
 Collection of homogenous elements referred by
single name
 Mathematical problems like linear algebra can
easily be handled by 2-dimensional arrays
Dr. Hanif Durad 4

5. 5
3.3 One-Dimensional Arrays (1/2)
 Suppose, you need to store years of 100 cars.
Will you define 100 variables?
int y1, y2,…, y100;
 An array is an indexed data structure to represent
several variables having the same data type: int
y[100];
y[0] y[1] y[2] … y[k-1] y[k] y[k+1] … y[98] y[99]
D:Data StructuresHanif_SearchArrays and Matrices Chap5.ppt

6. 6
One-Dimensional Arrays (2/2)
 An element of an array is accessed using the
array name and an index or subscript, for
example: y[5] which can be used like a variable
 In C, the subscripts always start with 0 and
increment by 1, so y[5] is the sixth element
 The name of the array is the address of the first
element and the subscript is the offset
y[0] y[1] y[2] … y[k-1] y[k] y[k+1] … y[98] y[99]

7. 7
3.2 Definition and Initialization
 An array is defined using a declaration
statement.
data_type array_name[size];
 allocates memory for size elements
 subscript of first element is 0
 subscript of last element is size-1
 size must be a constant

8. 8
Example
int list[5];
 allocates memory for 5 integer variables
 subscript of first element is 0
 subscript of last element is 4
 C does not check bounds on arrays
 list[6] =5; /* may give segmentation fault or
overwrite other memory locations*/
list[0]
list[1]
list[2]
list[3]
list[4]

9. 9
Initializing Arrays
 Arrays can be initialized at the time they are
declared.
 Examples:
double taxrate[3] ={0.15, 0.25, 0.3};
char list[5] = {‘h’, ’e’, ’l’, ’l’, ’o’};
double vector[100] = {0.0}; /* assigns
zero to all 100 elements */
int s[] = {5,0,-5}; /*the size of s is 3*/

10. 10
Assigning values to an array
For loops are often used to assign values to an array
Example:
int list[5], i;
for(i=0; i<5; i++){
list[i] = i;
} list[0]
list[3]
list[4]
list[1]
list[2]
0
1
2
3
4
list[0]
list[1]
list[2]
list[3]
list[4]
OR
for(i=0; i<=4; i++){
list[i] = i;
}

11. 11
Assigning values to an array
Give a for loop to assign the below values to list
int list[5], i;
for(i=0; i<5; i++){
list[i] = 4-i;
}
list[0]
list[3]
list[4]
list[1]
list[2]
4
3
2
1
0

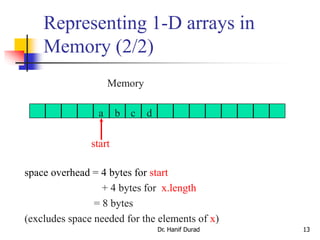
12. 3.4 Representing 1-D arrays in
Memory (1/2)
Dr. Hanif Durad 12
 1-dimensional array x = [a, b, c, d]
 map into contiguous memory locations
Memory
a b c d
start
• location(x[i]) = start + i
D:Data StructuresCSED232lecture3-array.ppt

13. Representing 1-D arrays in
Memory (2/2)
Dr. Hanif Durad 13
space overhead = 4 bytes for start
+ 4 bytes for x.length
= 8 bytes
(excludes space needed for the elements of x)
Memory
a b c d
start

14. 3.5 Operations on arrays
 Traversing
 Insertion
 Deletion
 Searching
 Concatenation
 Merging
 Inversion
 Sorting
Dr. Hanif Durad 14

15. 3.6 Limitations Of Linear Arrays
 The prior knowledge of no. of elements in the linear
array is necessary
 These are static structures static in the sense that
memory is allocated at compilation time, their memory
used by them can’t be reduced or extended
 Since the elements of this arrays are stored in these
arrays are time consuming this is because of moving
down or up to create a space of new element or to
occupy the space vacated by deleted element
Dr. Hanif Durad 15

16. 3.7 Multidimensional Arrays
 An array can have many dimensions – if it has more than
one dimension, it is called a multidimensional array
 Each dimension subdivides the previous one into the
specified number of elements
 Each dimension has its own length
 Memory requirement changes drastically, can result in
shortage of memory
e.g.
int X [3] [4] [5];
Dr. Hanif Durad 16
D:Data StructuresHanif_SearchArrays and Matrices20080714_MultiD.ppt+
D:Data StructuresHanif_SearchArrays and MatricesMultidimensional Arrays.ppt

17. 3.8 2-D Arrays
The elements of a 2-dimensional array a
declared as:
int a[3][4];
may be shown as a table
a[0][0] a[0][1] a[0][2] a[0][3]
a[1][0] a[1][1] a[1][2] a[1][3]
a[2][0] a[2][1] a[2][2] a[2][3]
Dr. Hanif Durad 17
D:Data StructuresCSED232lecture4-arrays.ppt

18. Rows of a 2D Array
Dr. Hanif Durad 18
a[0][0] a[0][1] a[0][2] a[0][3] row 0
a[1][0] a[1][1] a[1][2] a[1][3] row 1
a[2][0] a[2][1] a[2][2] a[2][3] row 2

19. Columns of a 2D Array
Dr. Hanif Durad 19
a[0][0] a[0][1] a[0][2] a[0][3]
a[1][0] a[1][1] a[1][2] a[1][3]
a[2][0] a[2][1] a[2][2] a[2][3]
column 0 column 1 column 2 column 3

20. 2D Array Representation in C++
view 2D array as a 1D array of rows
x = [row0, row1, row 2]
row 0 = [a, b, c, d]
row 1 = [e, f, g, h]
row 2 = [i, j, k, l]
and store as 4 1D arrays
2-dimensional array x
a, b, c, d
e, f, g, h
i, j, k, l

21. 2D Array Representation in C++
a b c d
e f g h
i j k l
x[]
4 separate
1-dimensional arrays
 space overhead = overhead for 4 1D arrays
= 4 * 4 bytes
= 16 bytes
= (number of rows + 1) x 4 bytes

22. Array Representation in C++
 This representation is called the array-of-arrays representation.
 Requires contiguous memory of size 3, 4, 4, and 4 for the 4 1D
arrays.
 1 memory block of size number of rows and number of rows
blocks of size number of columns
a b c d
e f g h
i j k l
x[]

23. Row-Major Mapping
 Example 3 x 4 array:
a b c d
e f g h
i j k l
 Convert into 1D array y by collecting elements by rows.
 Within a row elements are collected from left to right.
 Rows are collected from top to bottom.
 We get y[] = {a, b, c, d, e, f, g, h, i, j, k, l}
row 0 row 1 row 2 … row i
3.9 Representing 2-D arrays in Memory

24. Locating Element x[i][j]
 assume x has r rows and c columns
 each row has c elements
 i rows to the left of row i
 so ic elements to the left of x[i][0]
 x[i][j] is mapped to position
ic + j of the 1D array
row 0 row 1 row 2 … row i
0 c 2c 3c ic
3.10 Address Calculation for 2-D Array

25. Space Overhead
4 bytes for start of 1D array +
4 bytes for c (number of columns)
= 8 bytes
Note that we need contiguous memory of size rc.
row 0 row 1 row 2 … row i

26. Column-Major Mapping
a b c d
e f g h
i j k l
 Convert into 1D array y by collecting elements by
columns.
 Within a column elements are collected from top to
bottom.
 Columns are collected from left to right.
 We get y = {a, e, i, b, f, j, c, g, k, d, h, l}

27. 27
Row- and Column-Major
Mappings
2D Array int a[3][6];
a[0][0] a[0][1] a[0][2] a[0][3] a[0][4] a[0][5]
a[1][0] a[1][1] a[1][2] a[1][3] a[1][4] a[1][5]
a[2][0] a[2][1] a[2][2] a[2][3] a[2][4] a[2][5]

28. 28
Row- and Column-Major
Mappings
 Row-major order mapping functions
map(i1,i2) = i1u2+i2 for 2D arrays
map(i1,i2,i3) = i1u2u3+i2u3+i3 for 3D arrays

29. 29
Matrices
 m x n matrix is a table with m rows and n columns.
 M(i,j) denotes the element in row i and column j.
 Common matrix operations
 transpose
 addition
 multiplication

30. 30
Matrix Operations
 Transpose
 The result of transposing an m x n matrix is an n x m
matrix with property:
MT(j,i) = M(i,j), 1 <= i <= m, 1 <= j <= n
 Addition
 The sum of matrices is only defined for matrices that
have the same dimensions.
 The sum of two m x n matrices A and B is an m x n
matrix with the property:
C(i,j) = A(i,j) + B(i,j), 1 <= i <= m, 1 <= j <= n

31. 31
Matrix Operations
 Multiplication
 The product of matrices A and B is only defined
when the number of columns in A is equal to the
number of rows in B.
 Let A be m x n matrix and B be a n x q matrix. A*B
will produce an m x q matrix with the following
property:
C(i,j) = Σ(k=1…n) A(i,k) * B(k,j)
where 1 <= i <= m and 1 <= j <= q

32. 32
Special Matrices
 A square matrix has the same number of rows and
columns.
 Some special forms of square matrices are
 Diagonal: M(i,j) = 0 for i ≠ j
 Tridiagonal: M(i,j) = 0 for |i-j| < 1
 Lower triangular: M(i,j) = 0 for i < j
 Upper triangular: M(i,j) = 0 for i > j
 Symmetric M(i,j) = M(j,i) for all i and j
D:Data StructuresCSED232 lecture4-matrix.ppt

33. 33
Special Matrices

34. 34
Special Matrices
 Why are we interested in these “special”
matrices?
 We can provide more efficient implementations for
specific special matrices.
 Rather than having a space complexity of O(n2), we
can find an implementation that is O(n).
 We need to be clever about the “store” and “retrieve”
operations to reduce time.

35. 35
Diagonal Matrix
 Naive way to represent n x n diagonal matrix
 requires n2 x sizeof (T) bytes of memory where T is
the data type of elements
 Better way
 a[i-1]= 0 for D(i,j) where i = j
0 for D(i,j) where i ≠ j
 requires n x sizeof(T) bytes of memory
DS-1, P-95

36. 36
Tridiagonal Matrix
 Nonzero elements lie on one of three diagonals:
 main diagonal: i = j (=n)
 diagonal below main diagonal: i = j+1(=n-1)
 diagonal above main diagonal: i = j-1(=n-1)
 3n-2 elements on these three diagonals:

37. 37
Triangular Matrix
 Nonzero elements lie in the region marked
“nonzero” in the figure below
 1+2+…+n = Σ(i=1..n) = n(n+1)/2 elements in the
nonzero region

38. 38
Symmetric Matrix
 An n x n matrix can be represented using 1-D array of
size n(n+1)/2 by storing either the lower or upper
triangle of the matrix
 Use one of the methods for a triangular matrix
 The elements that are not explicitly stored may be
computed from those that are stored
 How do we compute this?

39. 39
Sparse Matrix
 A matrix is sparse if many of its elements are zero
 A matrix that is not sparse is dense
 The boundary is not precisely defined
 Diagonal and tridiagonal matrices are sparse
 We classify triangular matrices as dense
 Two possible representations
 array
 linked list

40. 40
Array Representation of Sparse
Matrix
 The nonzero entries may be mapped into a 1D array in
row-major order
 To reconstruct the matrix structure, need to record the
row and column each nonzero comes from
(RCV)

41. Linked Representation of Sparse
Matrix (1/2)
 A shortcoming of the 1-D array of a sparse
matrix is that we need to know the number of
nonzero terms in each of the sparse matrices
when the array is created
 A linked representation can overcome this
shortcoming
Dr. Hanif Durad 41

42. Linked Representation of Sparse
Matrix (2/2)
 A sparse matrix using linked list requires three
structures:
 Head node
 Row node
 Column Node
Dr. Hanif Durad 42

43. 43
•
Linked Representation of Sparse
Matrix

44. 44
•
Linked Representation of Sparse
Matrix
84 9
No. of rows
No. columns
No. columns

45. Strings in C
D:C LanguageLecturesChapter4_c.ppt

46. Strings
 Character type array is called string. All
strings end with the NULL character. Use
the %s placeholder in the printf() function
to display string values.
 Declaration:
char name[50];
Dr. Hanif Durad 46
http://lectures-c.blogspot.com/2009/02/strings-in-c.html

47. Example -1
#include
void main (void )
{
char *st1 = "abcd";
char st2[] = "efgh";
printf( "%sn", st1);
printf( "%sn", st2);
}
Dr. Hanif Durad 47
string1.c

48. Example-2
void main(void){
char myname[] = { ‘H', ‘a', ‘n', ‘i', ‘f' };
printf("%s n",myname);
}
Dr. Hanif Durad 48
string2.c

49. String input and output:
 gets function relieves the string from standard input device
while puts outputs the string to the standard output device.
 The function gets accepts the name of the string as a parameter,
and fills the string with characters that are input from the
keyboard till newline character is encountered.
 The syntax of the gets function is
gets (str_var);
 The puts function displays the contents stored in its parameter
on the standard screen.
 The syntax of the puts character is
puts (str_var);
Dr. Hanif Durad 49

50. Example-3
#include <stdio.h>
# include <string.h>
void main ( )
{
char myname [40];
printf ("Type your Name :");
gets (myname);
printf ("Your name is :");
puts(myname);
}
Dr. Hanif Durad 50
string3.c

51. Some String Functions:
Dr. Hanif Durad 51
Function Description
strcpy(string1, string2) Copy string2 into string1
strcat(string1, string2) Concatenate string2 onto the end of string1
length = strlen(string) Get the length of a string
strcmp(string1,
string2)
Return 0 if string1 equals string2, otherwise
nonzero
strchr(string1, chr); will find the first matching character in a string