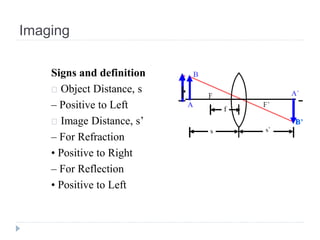
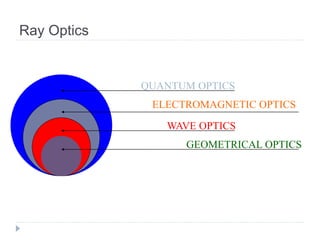
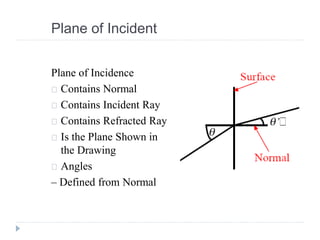
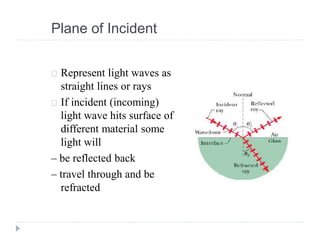
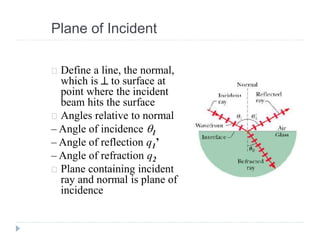
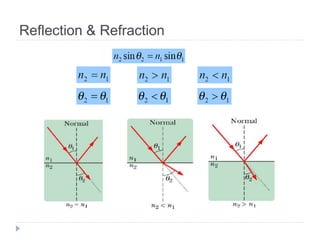
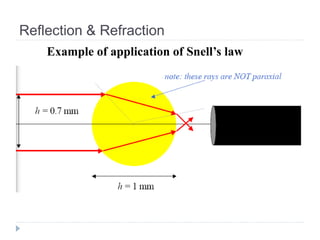
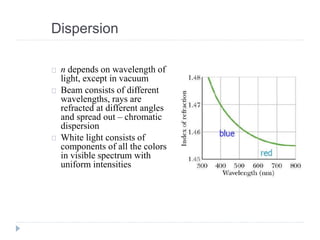
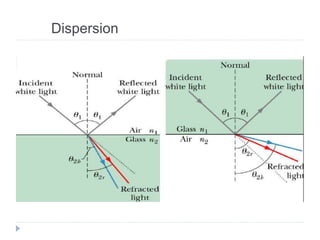
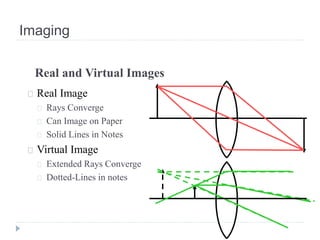
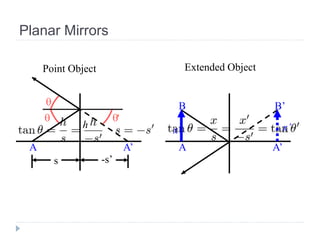
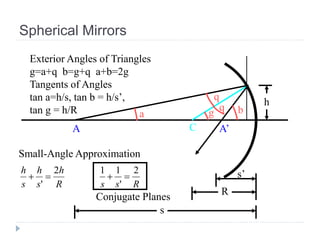
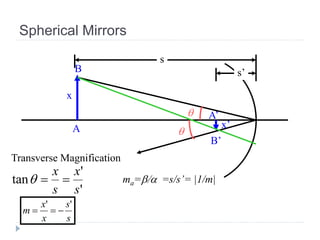
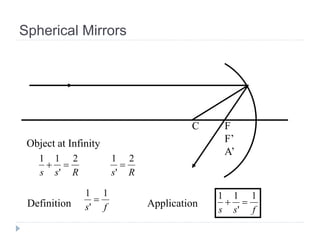
This document summarizes key concepts in geometrical optics, including: - Ray optics approximates light propagation using rays and geometric rules. Reflection and refraction at an interface follow laws like Snell's law. - Plane mirrors form virtual, erect images. Spherical mirrors form real images that are inverted with magnification determined by the mirror equation. - Lenses are analyzed similarly using conjugate planes and the lensmaker's equation. They can form real or virtual images, magnified or demagnified, depending on object and image distances.

1. Optics – geometrical optics

2. Contents
Postulates of ray optics
Optical components
-Mirrors
-Lenses
-Stops and pupils
Matrix optics

3. Ray Optics
Ray optics is the simplest theory of light
Light is described by rays that travel in different optical
media in accordance with a set of geometrical rules
Ray optics is also known as Geometrical Optics
Useful for studying image formation

4. Ray Optics
QUANTUM OPTICS
ELECTROMAGNETIC OPTICS
WAVE OPTICS
GEOMETRICAL OPTICS

5. Postulates of Ray Optics
Light travels in the form of rays
An optical medium is characterized by a quantity
called refractive index, which is the ratio of speed of
light in free space to that in the medium
The optical path length,
The optical path length corresponds to the
distance in vacuum equivalent to the distance
transverse in the medium of index n.

6. The time taken by light to travel from point S to P is
proportional to the optical path length
Fermat’s Principle
- Light, in going from point S to P, traverses the route
having the smallest optical path length or shortest
time. Derivative of OPL is zero.
- Governs the laws of refraction & reflection
Postulates of Ray Optics

7. Plane of Incident
Plane of Incidence
Contains Normal
Contains Incident Ray
Contains Refracted Ray
Is the Plane Shown in
the Drawing
Angles
– Defined from Normal

8. Represent light waves as
straight lines or rays
If incident (incoming)
light wave hits surface of
different material some
light will
– be reflected back
– travel through and be
refracted
Plane of Incident

9. Define a line, the normal,
which is  to surface at
point where the incident
beam hits the surface
Angles relative to normal
– Angle of incidence 1
– Angle of reflection q1’
– Angle of refraction q2
Plane containing incident
ray and normal is plane of
incidence
Plane of Incident

10. Reflection & Refraction
Law of reflection: Reflected ray lies in plane of
incidence and angle for reflection is equal to
angle of incidence

11. Law of refraction: Refracted ray lies in plane of
incidence and angle of refraction is related to angle
of incidence by Snell’s law
n is dimensionless constant called index of
refraction. Index of refraction, n for given medium
is defined as
Reflection & Refraction

12. Exercise
Use Fermat’s principle to derive the law of reflection and
law of refraction.

13. Reflection & Refraction

14. Reflection & Refraction
Example of application of Snell’s law

15. Exercise
A beam of collimated light traveling in air makes an angle of
30o to the normal of a glass plate. If the index of the glass is
ng = 3/2, determine the direction of the transmitted beam
within the plate.

16. Reflection & Refraction
The angle of incidence which causes the refracted ray
to point directly along the surface is called the critical
angle, qc
Angles larger than qc, no light is refracted, so we have
total internal reflection (TIR)
For total internal reflection to occur
n2 < n1
– E.g. moving from water into air
– Will not happen if moving from
air into water

17. Dispersion
n depends on wavelength of
light, except in vacuum
Beam consists of different
wavelengths, rays are
refracted at different angles
and spread out – chromatic
dispersion
White light consists of
components of all the colors
in visible spectrum with
uniform intensities

18. Dispersion

19. Imaging
First, Assume a Point Object
Spherical Wavefronts and Radial Rays
Define Object Location
Find Image Location
Real or Virtual?
Next Assume an Extended Object
Compute Magnification
Transverse, Longitudinal, Angular

20. Signs and definition
Object Distance, s
– Positive to Left
Image Distance, s’
– For Refraction
• Positive to Right
– For Reflection
• Positive to Left
B’
Imaging

21. Imaging
Real Image
Rays Converge
Can Image on Paper
Solid Lines in Notes
Virtual Image
Extended Rays Converge
Dotted-Lines in notes
Real and Virtual Images

22. Planar Mirrors
Point Object Extended Object


A A’
-s’s

A A’
B B’
h
x x’
‘

23. Planar Mirrors
x’=x m=x’/x=1
Transverse Magnification
ds’=-ds mz=ds’/ds=-1
Longitudinal Magnification
q’=q ma=q’/q =1
Angular Magnification
Image is
Virtual (Dotted lines converge)
Erect (m>0),
Perverted (cannot rotate to object)
but not distorted (|m|=|mz|)

24. Spherical Mirrors
CA A’
q
q
a bg
s
s’
R
h
Small-Angle Approximation
R
h
s
h
s
h 2
'

Rss
2
'
11

Conjugate Planes
Exterior Angles of Triangles
g=a+q b=g+q a+b=2g
Tangents of Angles
tan a=h/s, tan b = h/s’,
tan g = h/R

25. Spherical Mirrors
A
A’
s
s’B
B’
Transverse Magnification
'
'
tan
s
x
s
x

s
s
x
x
m
''

ma=b/a =s/s’= |1/m|
x
x’



26. Spherical Mirrors
2
''







s
s
ds
ds
mz
Image is
Real (Converging Rays),
Inverted (m<0),
Distorted (mz=-m2),
but Not Perverted (sign(m)=sign(mz))
ma=b/a =s/s’= |1/m|
Transverse Magnification
Longitudinal Magnification
Angular Magnification
s
s
x
x
m
''
-==
Rss
2
'
11
  
0
'
'
22




s
ds
s
ds
Image Equation Differentiate
2
''







s
s
ds
ds
mz
Longitudinal Magnification

27. Spherical Mirrors
F
F’
A’
Object at Infinity
Rss
2
'
11

Rs
2
'
1

fs
1
'
1
Definition Application
fss
1
'
11

C

28. Exercise
Show that a spherical mirror equation is applicable to a
planar reflecting surface.
A one-inch tall candle is set three inches in front of a
concave spherical mirror having a one-foot radius.
Describe the resulting image.