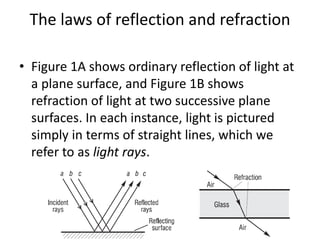
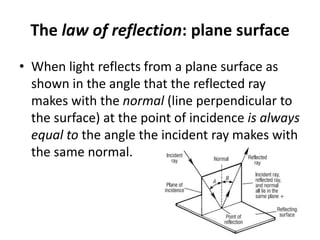
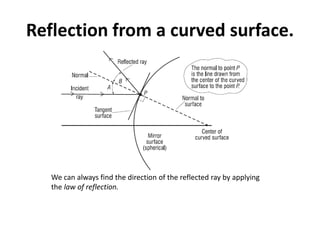
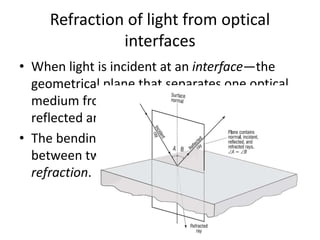
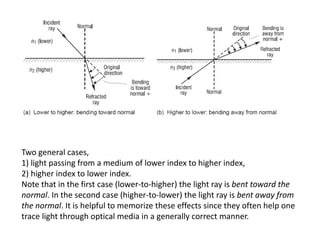
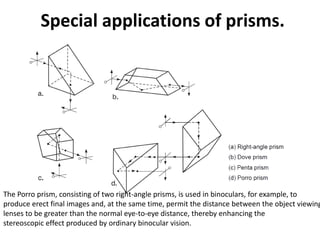
Geometrical optics describes the laws of reflection and refraction of light. When light travels from one medium to another, it can be reflected, refracted, scattered, or absorbed at the interface. Reflection follows the law that the angle of incidence equals the angle of reflection. Refraction is described by Snell's law, which relates the sines of the angles of incidence and refraction to the refractive indices of the media. The bending of light occurs due to changes in speed as it passes between materials of different refractive indices. Prisms are used to demonstrate refraction and dispersion of light into its component wavelengths.

1. Geometrical optics

2. The laws of reflection and refraction
• Figure 1A shows ordinary reflection of light at
a plane surface, and Figure 1B shows
refraction of light at two successive plane
surfaces. In each instance, light is pictured
simply in terms of straight lines, which we
refer to as light rays.

3. Reflection of light from optical
surfaces
• When light is incident on an interface between
two transparent optical media—such as between
air and glass or between water and glass—four
things can happen to the incident light.
– It can be partly or totally reflected at the interface.
– It can be scattered in random directions at the
interface
– It can be partly transmitted via refraction at the
interface and enter the second medium.
– It can be partly absorbed in either medium.

4. The law of reflection: plane surface
• When light reflects from a plane surface as
shown in the angle that the reflected ray
makes with the normal (line perpendicular to
the surface) at the point of incidence is always
equal to the angle the incident ray makes with
the same normal.

5. Reflection from a curved surface.
We can always find the direction of the reflected ray by applying
the law of reflection.

6. Refraction of light from optical
interfaces
• When light is incident at an interface—the
geometrical plane that separates one optical
medium from another—it will be partly
reflected and partly transmitted.
• The bending of light rays at an interface
between two optical media is called
refraction.

7. Refractive Index
• The two transparent optical media that form an
interface are distinguished from one another by a
constant called the index of refraction, generally
labelled with the symbol n.
• The index of refraction for any transparent optical
medium is defined as the ratio of the speed of light
in a vacuum to the speed of light in the medium, as
given as

8. Indexes of Refraction for Various
Materials at 589 nm
The greater the index of refraction of a medium, the lower
the speed of light in that medium and the more light is bent
in going from air into the medium

9. Two general cases,
1) light passing from a medium of lower index to higher index,
2) higher index to lower index.
Note that in the first case (lower-to-higher) the light ray is bent toward the
normal. In the second case (higher-to-lower) the light ray is bent away from
the normal. It is helpful to memorize these effects since they often help one
trace light through optical media in a generally correct manner.

10. Snell’s law
• Snell’s law of refraction relates the sines of the angles of
incidence and refraction at an interface between two optical
media to the indexes of refraction of the two media. The law
is named after a Dutch astronomer, Willebrord Snell, who
formulated the law in the 17th century.
• Snell’s law enables us to calculate the direction of the
refracted ray if we know the refractive indexes of the two
media and the direction of the incident ray. The mathematical
expression of Snell’s law and an accompanying drawing are
given as

11. • In practice Snell’s law is often written simply
as
ni sin i = nr sin r

12. Critical angle and total internal
reflection.
• When light travels from a medium of higher index to one of
lower index, we encounter some interesting results. where we
see four rays of light originating from point O in the higher-
index medium, each incident on the interface at a different
angle of incidence. Ray 1 is incident on the interface at 90°
(normal incidence) so there is no bending.

13. • Ray 1 no Deviation
• Ray 2 is incident at angle i and refracts (bends away from the
normal) at angle r
• Ray 3 is incident at the critical angle ic, large enough to cause
the refracted ray bending away from the normal (N) to bend
by 90°, thereby traveling along the interface between the two
media.
• Ray 4 is incident on the interface at an angle greater than the
critical angle, and is totally reflected into the same medium
from which it came.

14. Refraction in Prisms
• Glass prisms are often used to bend light in a
given direction as well as to bend it back again
(retroreflection). The process of refraction in
prisms is understood easily with the use of
light rays and Snell’s law

15. Minimum angle of deviation.
• It turns out that we can determine the
refractive index of a transparent material by
shaping it in the form of an isosceles prism
and then measuring its minimum angle of
deviation. With reference to, the relationship
between the refractive index n, the prism apex
angle A, and the minimum angle of deviation
δm is given by

16. Example

17. Dispersion of light.
• The variation of refractive index n with wavelength λ is called
dispersion.
• shows the separation of the individual colors in white light—400 nm to
700 nm— after passing through a prism

18. Special applications of prisms.
The Porro prism, consisting of two right-angle prisms, is used in binoculars, for example, to
produce erect final images and, at the same time, permit the distance between the object viewing
lenses to be greater than the normal eye-to-eye distance, thereby enhancing the
stereoscopic effect produced by ordinary binocular vision.