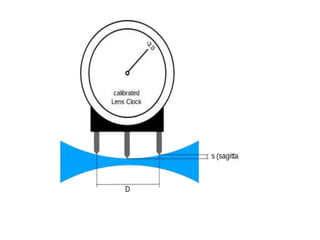
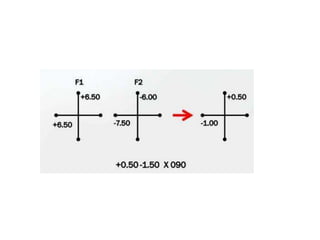
A lens clock is a mechanical device used to measure the curvature and optical power of a lens surface. It has three legs - two outer fixed legs and one inner movable leg. The difference in height between the inner and outer legs corresponds to the curvature of the lens surface. The lens clock converts this curvature measurement into a diopter value, assuming the lens material has a refractive index of 1.523. Rotating the lens clock allows measuring any cylindrical component of the lens. Adding the power readings from the front and back surfaces provides an estimate of the total lens power.

1. Lens gauge

2. Lens clock
• A lens clock is a mechanical dial indicator that is used to
measure dioptric power of a lens.
• It is a specialized version of a spherometer.
• A lens clock measures the curvature of a surface, but gives
the result as an optical power in dioptres, assuming the
lens is made of a material with a particular refractive index.
• It is called as Geneva Lens Gauge, Lens measure or Lens
Clock

4. Spherometer:
• A spherometer is an instrument for the
precise measurement of the radius of
curvature of a sphere or a curved surface.
Originally, these instruments were primarily
used by opticians to measure the curvature of
the surface of a lens.

5. Appearance
The lens clock has 3 legs
 The 2 outside legs do not move
 The center one moves in and out
 The difference in height position of the center leg
and the 2 outside leg is sag for the arc of a circle
Doesn’t show the actual sag measurement but shows the
dioptric value for the surface power

7. How it works: continue…………
• The lens clock has three pointed probes that
make contact with the surface of the lens. The
outer two probes are fixed while the center
one moves, retracting as the instrument is
pressed down on the lens's surface. As the
probe retracts, the hand on the face of the dial
turns by an amount proportional to the
distance.
• Use and measurements using a calibrated lens
clock
• The optical power ø of the surface is given by
ø=2(n-1)s /(D/2)²

8. • where n is the index of refraction of the
glass, s is the vertical distance (sagitta)
between the center and outer probes, and D is
the horizontal separation of the outer probes.
To calculate ø in diopters, both s and D must
be specified in meters.
How it works: continue…………

9. • A typical lens clock is calibrated to display the
power of a crown glass surface, with a refractive
index of 1.523. If the lens is made of some other
material, the reading must be adjusted to correct
for the difference in refractive index.
• Measuring both sides of the lens and adding the
surface powers together gives the approximate
optical power of the whole lens.
(This approximation relies on the assumption that the lens is
relatively thin.)
How it works: continue…………

10. Using The Lens Clock
• Place the clock on a flat surface, so that all 3 pins are
equal, your clock should measure zero– If not, your
lens clock is defective
• The lens clock must be held perpendicular to the
surface of the lens
• Tilting the clock by 10° from the perpendicular, can
create as much as 2 diopters of error in your reading.

11. Base Curve Determination
· Defined as the beginning curve upon which the net power is based
· The lens clock can be used to measure this
· Modern lenses have spherical front surfaces (F1)– The base curve
will be the lens clock reading of the front surface of the lens
· Back surface is called (F2)
· When measuring the F1 of the lens, you will need to read the black
scale
· When measuring the F2 of the lens, you will need to read the read scale
· If there are more than 1 curve on the front surface, the lens is either
warped or is a plus-cylinder lens form
· The base curve is the least curved of the 2 readings

12. Radius of curvature
• Radius of curvature R of the surface can be obtained from the
optical power given by the lens clock using the formula
R={(n-1)/ø
• where n is the index of refraction for which the lens clock is
calibrated, regardless of the actual index of the lens being
measured. If the lens is made of glass with some other index
n2 ᵢthe true optical power of the surface can be obtained
using
ø={(n2-1)/R

13. Radius of curvature continue……….
• Example—correcting for refractive index
• A biconcave lens made of flint glass with an index of 1.7 is measured with a lens clock calibrated
for crown glass with an index of 1.523. For this particular lens, the lens clock gives surface powers
of −3.0 and −7.0 diopters (dpt). Because the clock is calibrated for a different refractive index the
optical power of the lens is not the sum of the surface powers given by the clock. The optical
power of the lens is instead obtained as follows:
• First, the radii of curvature are obtained:
R1=(1.523-1) /-3.0 dpt =-0.174m
R2=(1.523-1) / -7.0 dpt =-0.0747m
• Next, the optical powers of each surface are obtained:
ø1=(1.7-1/-0.174m=-4.02dpt
ø2}=(1.7-1) /-0.0747m=-9.37dpt
• Finally, if the lens is thin the powers of each surface can be added to give the approximate optical
power of the whole lens: −13.4 diopters. The actual power, as read by a vertometer or lensometer,
might differ by as much as 0.1 diopters.

14. index
 The lens clock is designed for materials where n
= 1.53 (crown glass)
Measuring a lens where n > 1.53 – The lens clock
will read too LOW
Measuring a lens where n < 1.53 – The lens clock
will read too HIGH

15. Nominal Power of a Lens
Since the lens clock directly measures the surface values of
a lens, we can use it to approximate the power of lenses
– Only works for materials with index of refractions close to
1.53
· F1 measures +6.00D
· F2 measures -4.00D
· Ft = +2.00D (Power)

16. Power Determination
The lens clock can be used to measure sphere and cylinder power
1. Hold the lens clock so that the center leg is at the center of the lens and
perpendicular to the lens surface
2. Rotate the lens clock around the center leg
3. If the needle on the lens clock remains unchanged, the surface is
spherical
4. If the needle shows a change in value, the surface is toric with 2 separate
curves
5. Read the maximum and minimum values
(The orientation of the three legs where the maximum and minimum
readings are will correspond to the major meridians of lens power)
• Modern lenses are of Minus cylinder form. So while measuring the power
of the lens you might find cylinder in F2 and the F1 will always be
SPHERICAL

17. 1. When rotating the lens clock on the front surface of a lens, all
meridians read +4.00D. On the back surface, the clock reads -6.25D
Then the power will be
(+4.00) + (-6.25) = -2.25D
2. When rotating the lens clock on the front surface of a lens, all
meridians read +6.50D. On the back surface, the clock reads -7.50D
when the 3 legs are along the 180° meridian, and -6.00D when the 3
legs are along the 90°meridian. Here you can calculate the nominal
power of the lens if the lens made in minus cylinder form as given
below.