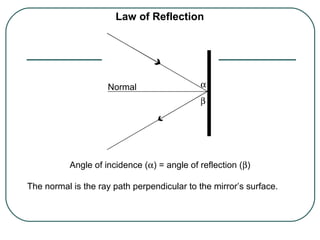
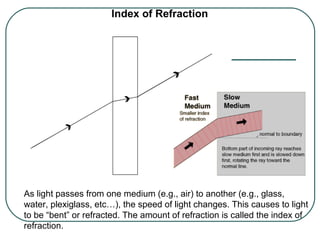
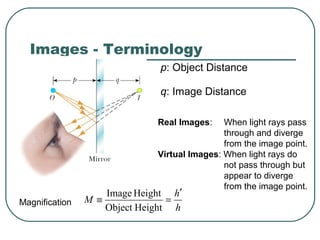
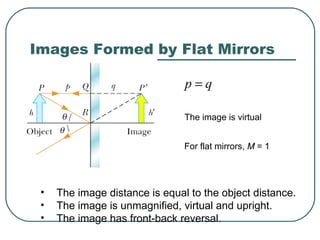
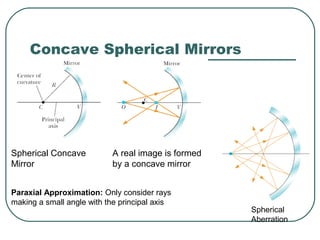
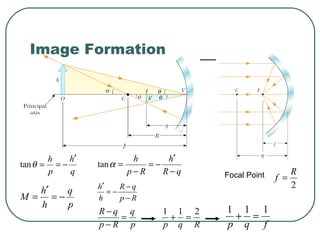
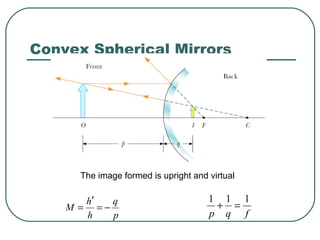
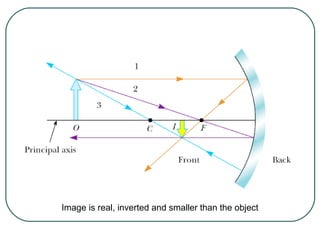
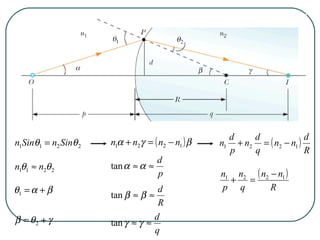
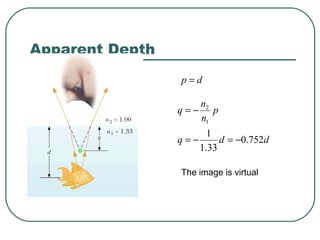
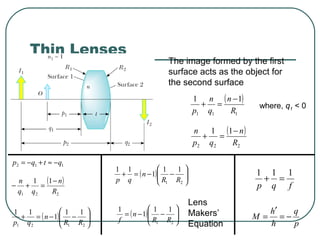
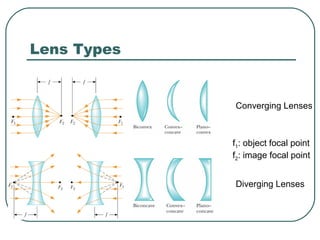
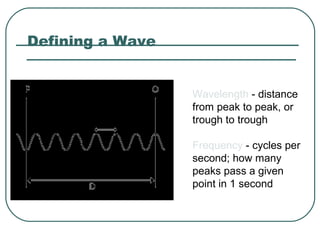
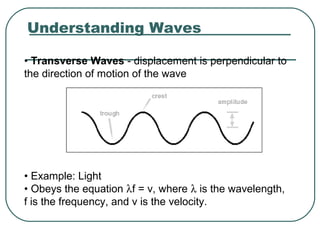
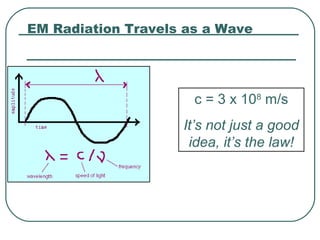
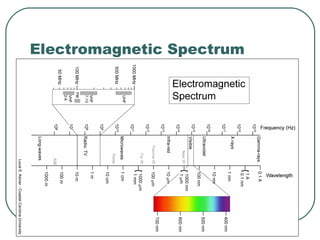
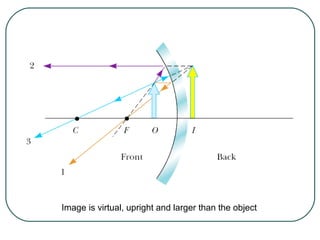
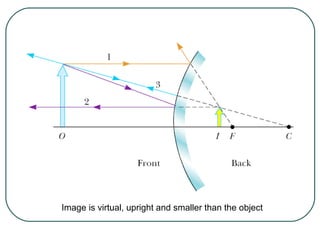
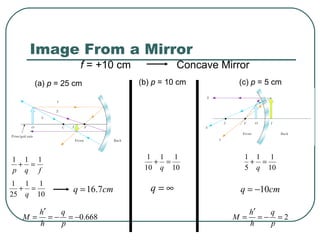
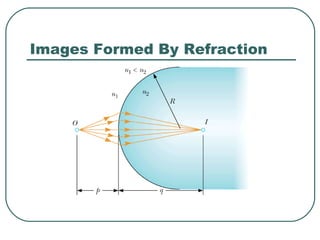
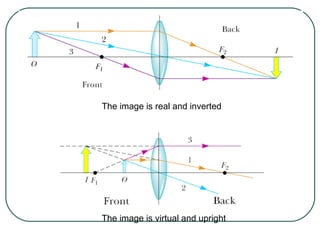
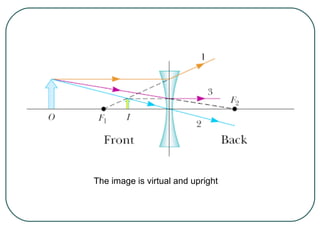
This document provides an overview of optics and light, including: 1) It defines key wave properties like wavelength and frequency, and describes longitudinal and transverse waves. 2) It introduces the electromagnetic spectrum and explains how different frequencies are classified. 3) It covers geometric optics concepts such as reflection, refraction, mirrors, lenses and image formation using ray diagrams. Sign conventions are also defined for analyzing optical systems.

1. Overview
 Waves
 Electromagnetic Spectrum
 Geometric Optics
• Mirrors
• Lenses
 Wave Optics

2. Defining a Wave
Wavelength - distance
from peak to peak, or
trough to trough
Frequency - cycles per
second; how many
peaks pass a given
point in 1 second

3. Understanding Waves
• Longitudinal waves - displacement is in same direction
as the wave motion
• Example: sound waves
• Obeys the equation λf = v, where λ is the wavelength,
n is the frequency, and v is the velocity.

4. Understanding Waves
• Transverse Waves - displacement is perpendicular to
the direction of motion of the wave
• Example: Light
• Obeys the equation λf = v, where λ is the wavelength,
f is the frequency, and v is the velocity.

5. Special Things About a
Light Wave
• It does not need a medium through which to travel
• It travels with its highest velocity in a vacuum
• Its highest velocity is the speed of light, c,
equal to 300,000 km/sec
• The frequency (or wavelength) of the wave determines
whether we call it radio, infrared, visible, ultraviolet,
X-ray or gamma-ray.

6. EM Radiation Travels as a Wave
c = 3 x 108
m/s
It’s not just a good
idea, it’s the law!

7. Waves Bring Us Information
About our Universe
• Different energies/frequencies/wavelengths produced by
different physical processes
Waves are how we perceive the world around us
- Sound waves = differences in pressure, hearing
- Light waves = sight
- Radio waves = communication

8. Electromagnetic Spectrum

9. ISNS 4371 Phenomena of Nature
Properties of Light
Law of Reflection - Angle of Incidence = Angle of reflection
Law of Refraction - Light beam is bent towards the normal
when passing into a medium of higher Index of Refraction.
Light beam is bent away from the normal
when passing into a medium of lower Index of Refraction.
Index of Refraction -
Inverse square law - Light intensity diminishes with square of
distance from source.
n=
Speedoflightinvacuum
Speedoflightinamedium

10. Normal
Law of Reflection
α
β
Angle of incidence (α) = angle of reflection (β)
The normal is the ray path perpendicular to the mirror’s surface.

11. Index of Refraction
As light passes from one medium (e.g., air) to another (e.g., glass,
water, plexiglass, etc…), the speed of light changes. This causes to light
to be “bent” or refracted. The amount of refraction is called the index of
refraction.

12. Refraction – Snell’s Law
•Snell’s law provides a way to determine the bending
of light as it goes from one medium to another.
•Total internal relfection: occurs when the angle of
refraction is greater than ninety degrees – all the light
is reflected!
n n1 1 2 2s i n s i nθ θ=

13. Geometric Optics
 Flat Mirrors
 Spherical Mirrors
 Images Formed by Refraction
 Thin Lenses
 Optical Instruments

14. Images - Terminology
p: Object Distance
q: Image Distance
Real Images: When light rays pass
through and diverge
from the image point.
Virtual Images: When light rays do
not pass through but
appear to diverge
from the image point.
h
h
M
′
=≡
HeightObject
HeightImage
Magnification

15. qp =
For flat mirrors, M = 1
• The image distance is equal to the object distance.
• The image is unmagnified, virtual and upright.
• The image has front-back reversal.
Images Formed by Flat Mirrors
The image is virtual

16. Concave Spherical Mirrors
Spherical Concave
Mirror
A real image is formed
by a concave mirror
Spherical
Aberration
Paraxial Approximation: Only consider rays
making a small angle with the principal axis

17. q
h
p
h ′
−==θtan
p
q
h
h
M −=
′
=
qR
h
Rp
h
−
′
−=
−
=αtan
Rp
qR
h
h
−
−
−=
′
p
q
Rp
qR
=
−
−
Rqp
211
=+
Focal Point
2
R
f =
fqp
111
=+
Image Formation

18. Convex Spherical Mirrors
The image formed is upright and virtual
p
q
h
h
M −=
′
=
fqp
111
=+

19. Sign Conventions for Mirrors
 p is positive if object is in front of mirror (real
object).
 p is negative if object is in back of mirror
(virtual object).
 q is positive if image is in front of mirror (real
image).
 q is negative if image is in back of mirror
(virtual image).
 Both f and R are positive if center of curvature
is in front of mirror (concave mirror).
 Both f and R are negative if center of curvature
is in back of mirror (convex mirror).
 If M is positive, image is upright.
 If M is negative, image is inverted.

20. Ray Diagrams For Mirrors
 Ray 1 is drawn from the top of the object
parallel to the principal axis and is
reflected through the focal point F.
 Ray 2 is drawn from the top of the object
through the focal point and is reflected
parallel to the principal axis.
 Ray 3 is drawn from the top of the object
through the center of curvature C and is
reflected back on itself.

21. Image is real, inverted and smaller than the object

22. Image is virtual, upright and larger than the object

23. Image is virtual, upright and smaller than the object

24. Image From a Mirror
f = +10 cm Concave Mirror
(a) p = 25 cm
fqp
111
=+
10
11
25
1
=+
q
668.0−=−=
′
=
p
q
h
h
M
cmq 7.16=
(b) p = 10 cm
10
11
10
1
=+
q
∞=q
(c) p = 5 cm
10
11
5
1
=+
q
cmq 10−=
2=−=
′
=
p
q
h
h
M

25. Images Formed By Refraction

26. 2211 θθ SinnSinn =
2211 θθ nn ≈
βαθ +=1
γθβ += 2
( )βγα 1221 nnnn −=+
p
d
≈≈ ααtan
R
d
≈≈ ββtan
q
d
≈≈ γγtan
( )
R
d
nn
q
d
n
p
d
n 1221 −=+
( )
R
nn
q
n
p
n 1221 −
=+

27. Sign Conventions for Refracting
Surfaces
 p is positive if object is in front of surface (real object).
 p is negative if object is in back of surface (virtual
object).
 q is positive if image is in back of surface (real image).
 q is negative if image is in front of surface (virtual
image).
 R is positive if center of curvature is in back of convex
surface.
 R is negative if center of curvature is in front of
concave surface.

28. Flat Refracting Surface
∞=R
021
=+
q
n
p
n
p
n
n
q
1
2
−=
The image is on the same side of the
surface as the object.

29. Apparent Depth
ddq
p
n
n
q
752.0
33.1
1
1
2
−=−=
−=
dp =
The image is virtual

30. Thin Lenses
The image formed by the first
surface acts as the object for
the second surface
( )
111
11
R
n
q
n
p
−
=+
( )
222
11
R
n
qp
n −
=+
where, q1 < 0
112 qtqp −≈+−=
( )
221
11
R
n
qq
n −
=+−
( ) 





−−=+
2121
11
1
11
RR
n
qp
( ) 





−−=+
21
11
1
11
RR
n
qp
( ) 





−−=
21
11
1
1
RR
n
f
Lens
Makers’
Equation
fqp
111
=+
p
q
h
h
M −=
′
=

31. Lens Types
Converging Lenses
Diverging Lenses
f1: object focal point
f2: image focal point

32. Sign Conventions for Thin Lenses
 p is positive if object is in front of lens (real object).
 p is negative if object is in back of lens (virtual object).
 q is positive if image is in back of lens (real image).
 q is negative if image is in front of lens (virtual image).
 R1 and R2 are positive if center of curvature is in back of lens.
 R1 and R2 are negative if center of curvature is in front of lens.
 f is positive if the lens is converging.
 f is negative if the lens is diverging.

33. Ray Diagrams for a Converging Lens
 Ray 1 is drawn parallel to the principal axis.
After being refracted, this ray passes through
the focal point on the back side of the lens.
 Ray 2 is drawn through the center of the lens
and continues in a straight line.
 Ray 3 is drawn through the focal point on the
front side of the lens (or as if coming from the
focal point if p < f) and emerges from the lens
parallel to the principal axis.

34. The image is virtual and upright
The image is real and inverted

35. Ray Diagrams for a Diverging Lens
 Ray 1 is drawn parallel to the principal axis.
After being refracted, this ray emerges such
that it appears to have passed through the
focal point on the front side of the lens.
 Ray 2 is drawn through the center of the lens
and continues in a straight line.
 Ray 3 is drawn toward the focal point on the
back side of the lens and emerges from the
lens parallel to the principal axis.

36. The image is virtual and upright

37. Combination of Thin Lenses
 First find the image created by the first lens as if the
second lens is not present.
 Then draw the ray diagram for the second lens with the
image from the first lens as the object.
 The second image formed is the final image of the
system.
f2f1
O
I1
I2