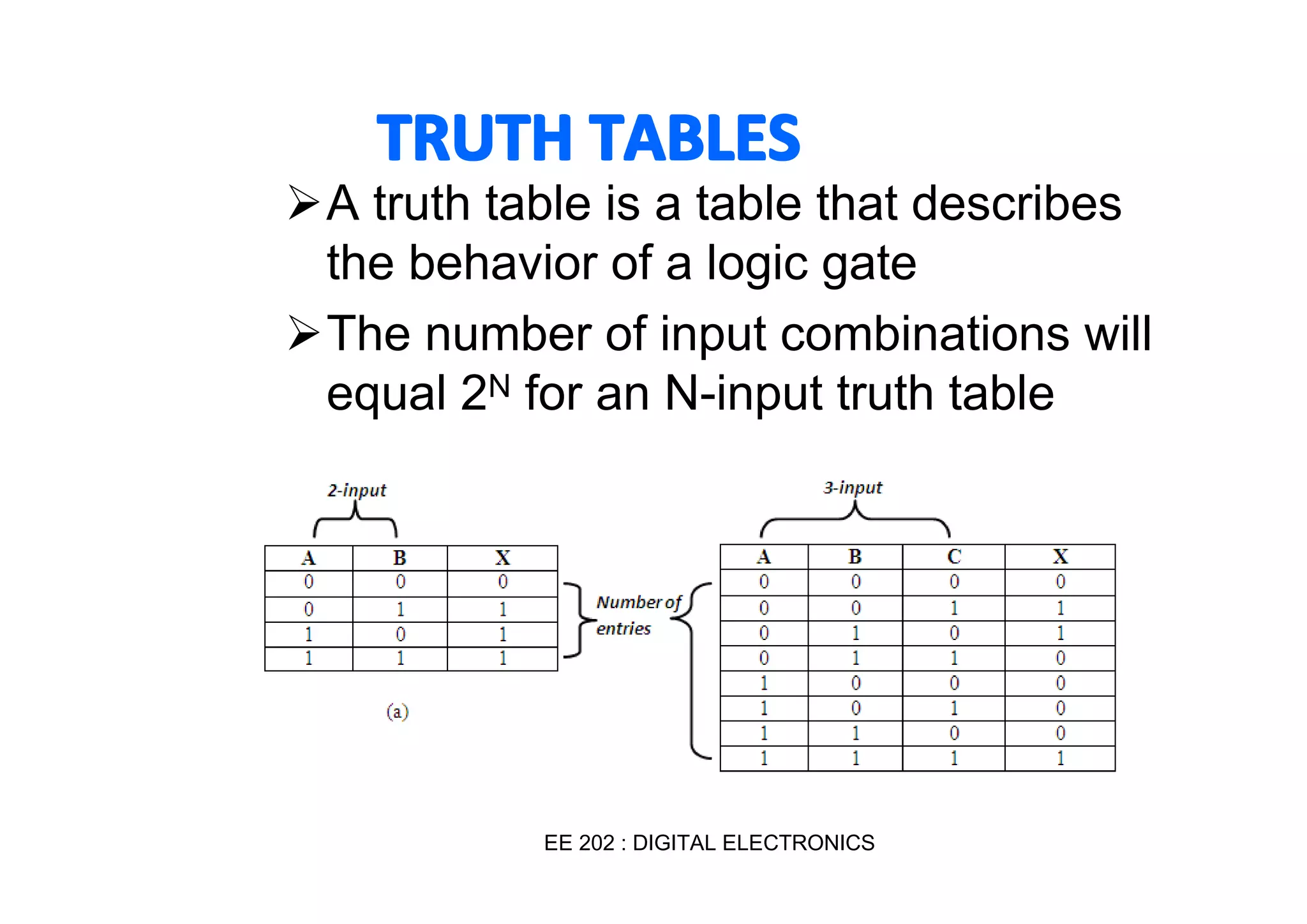
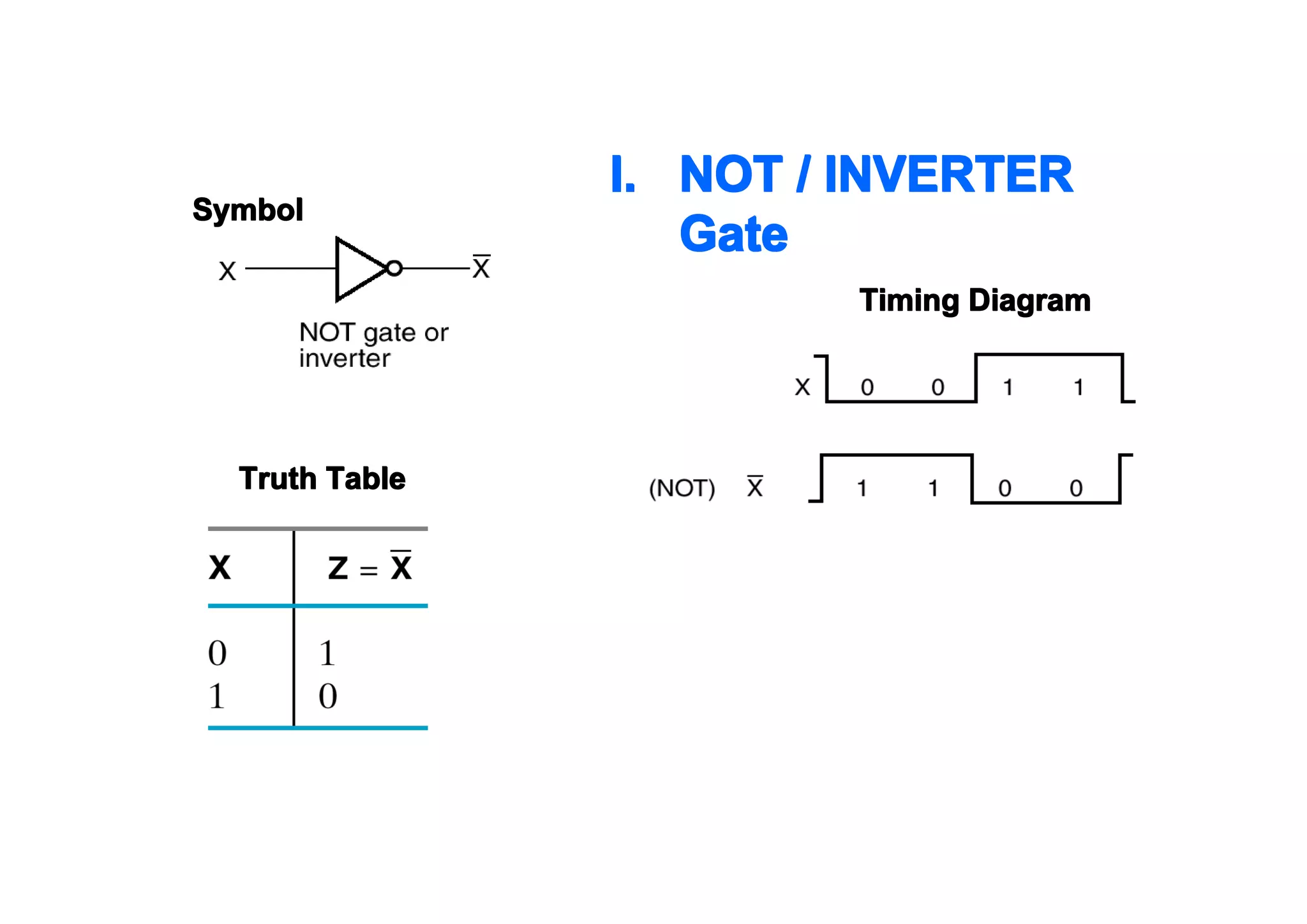
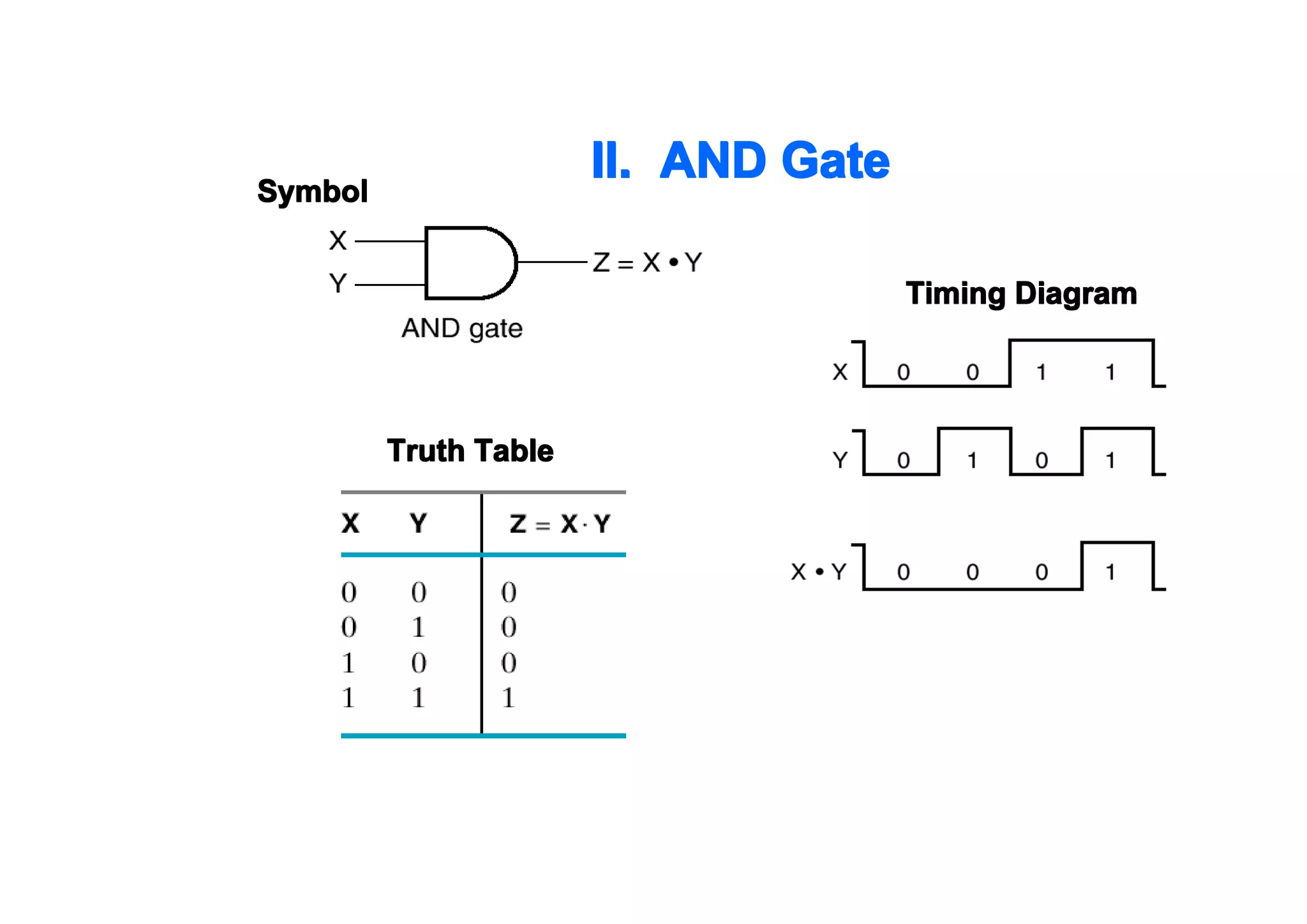
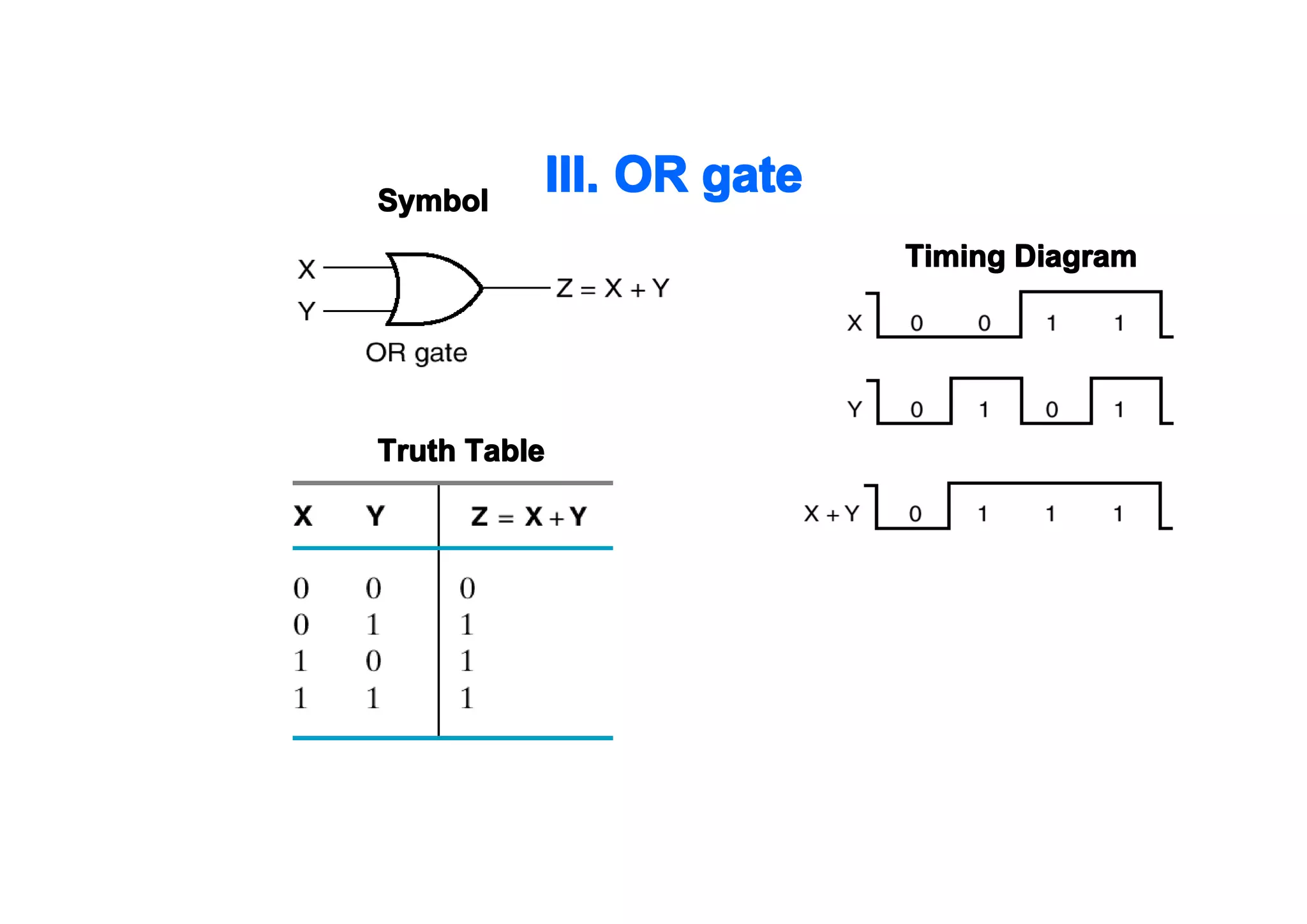
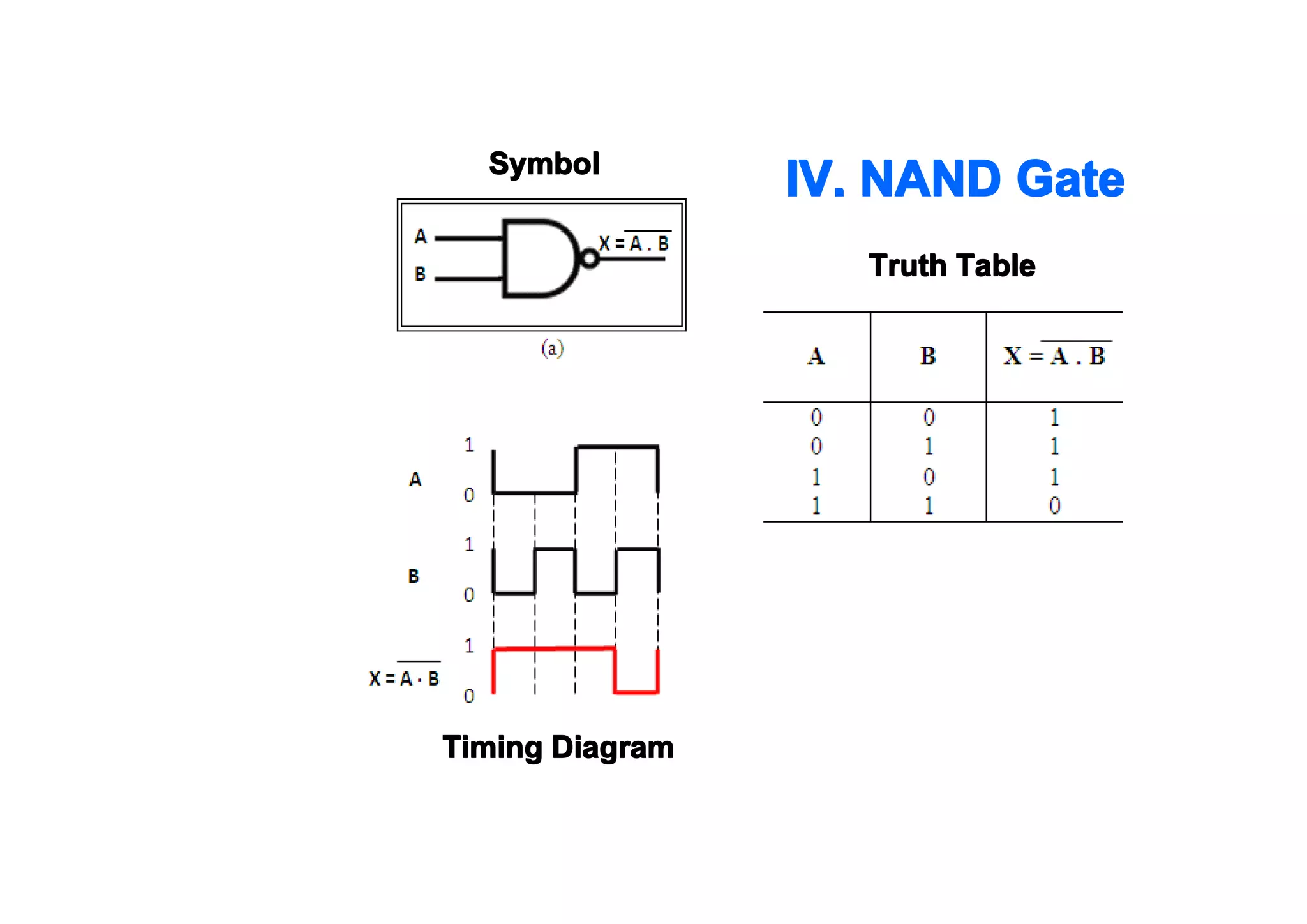
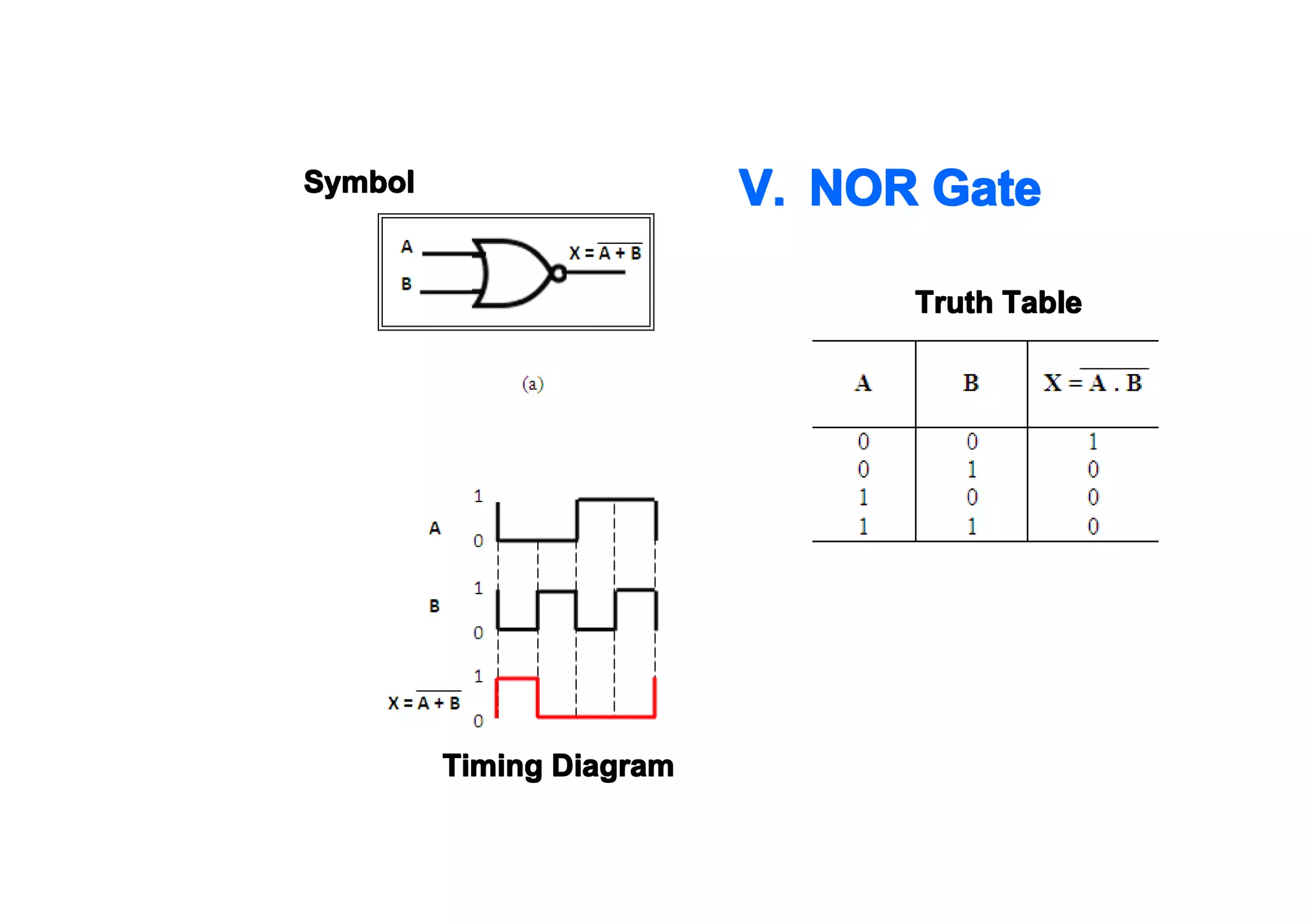
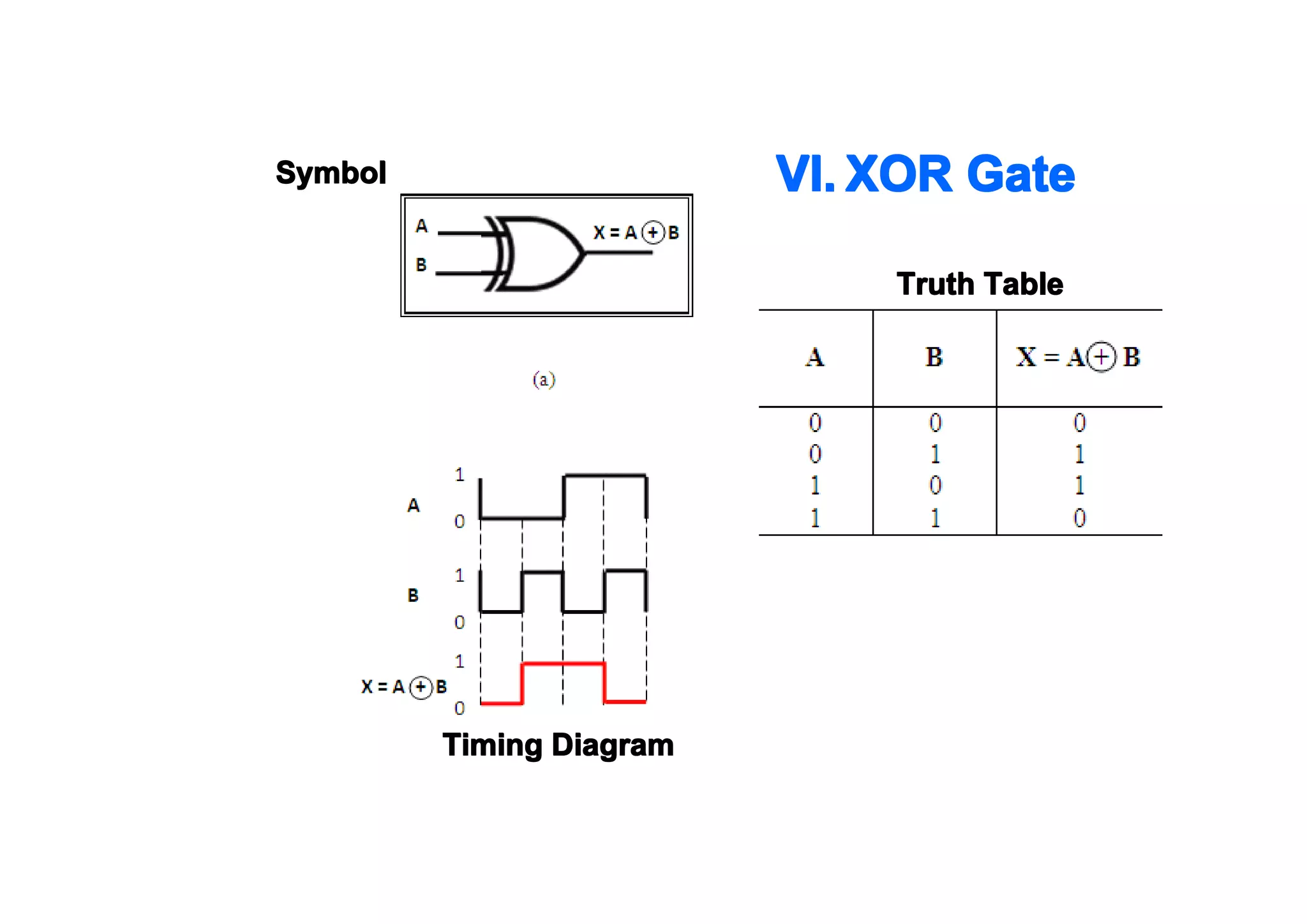
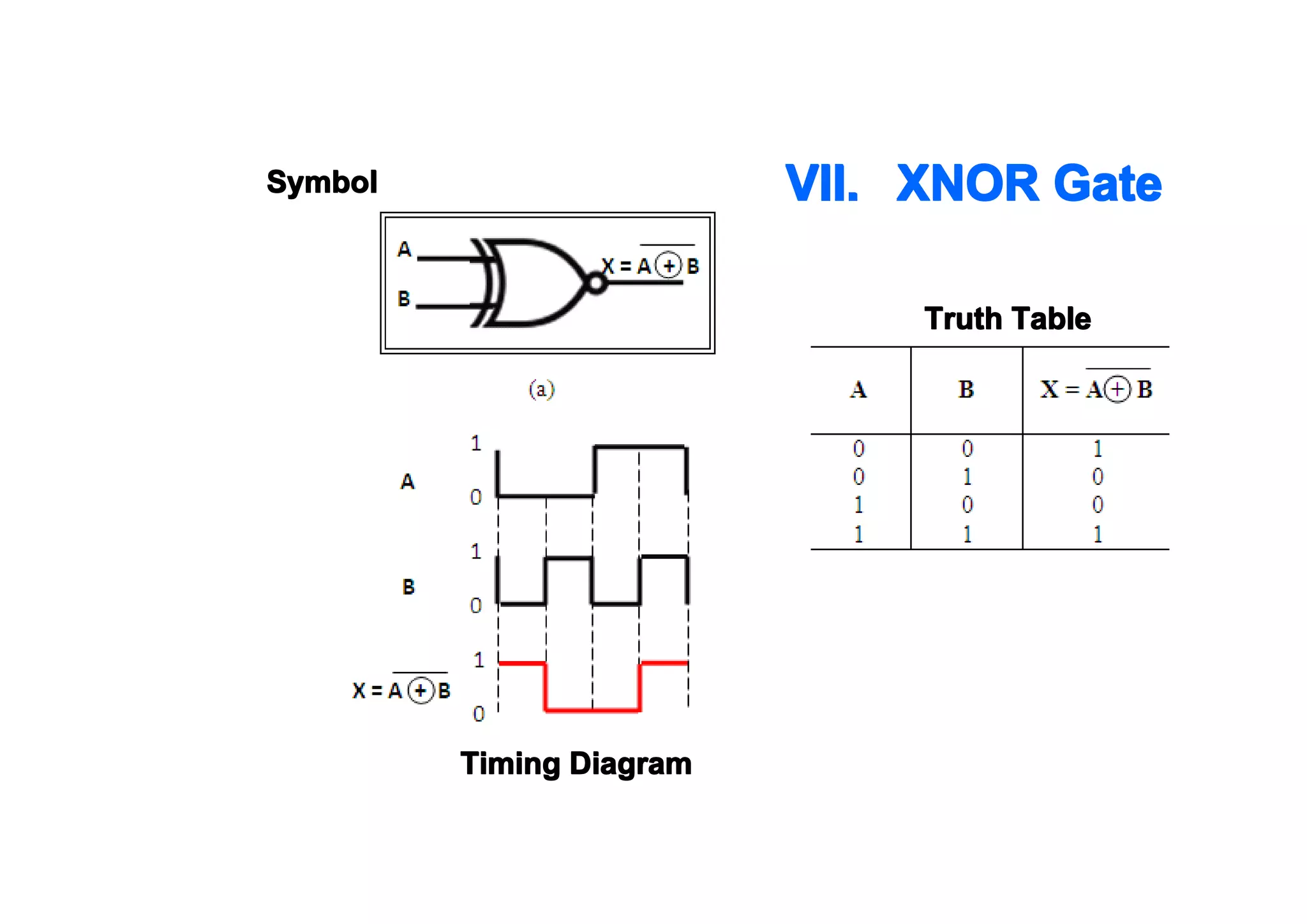
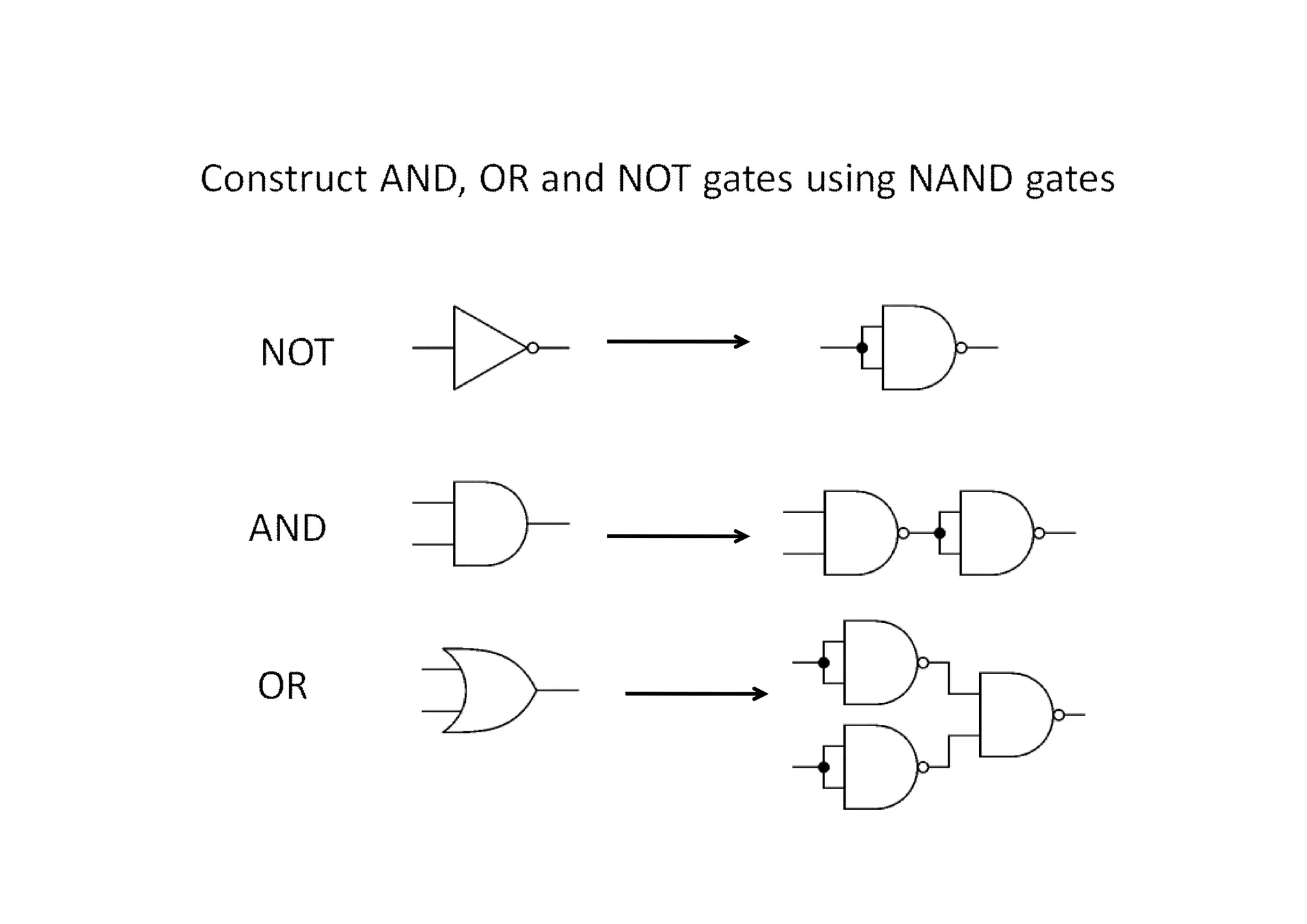
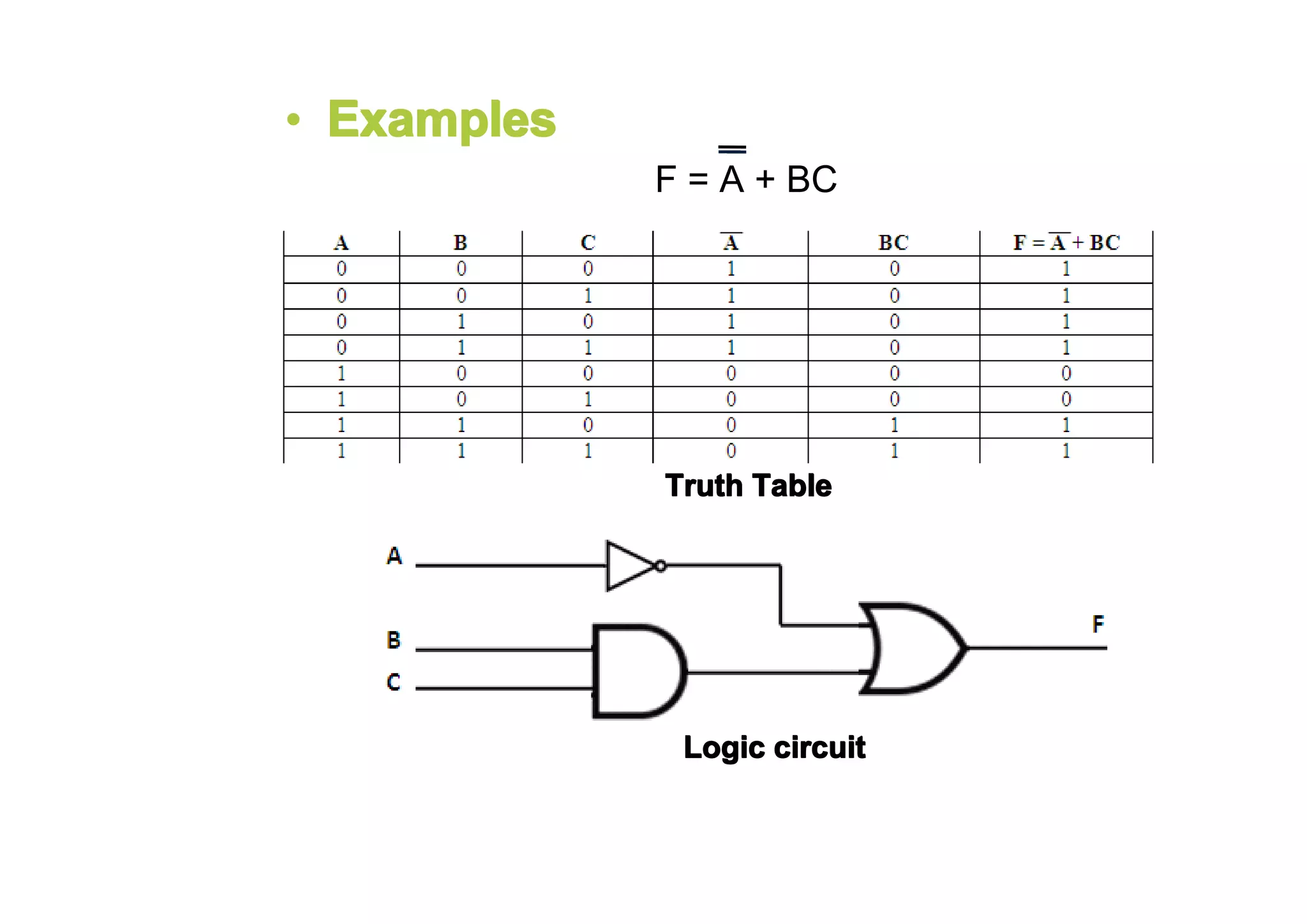
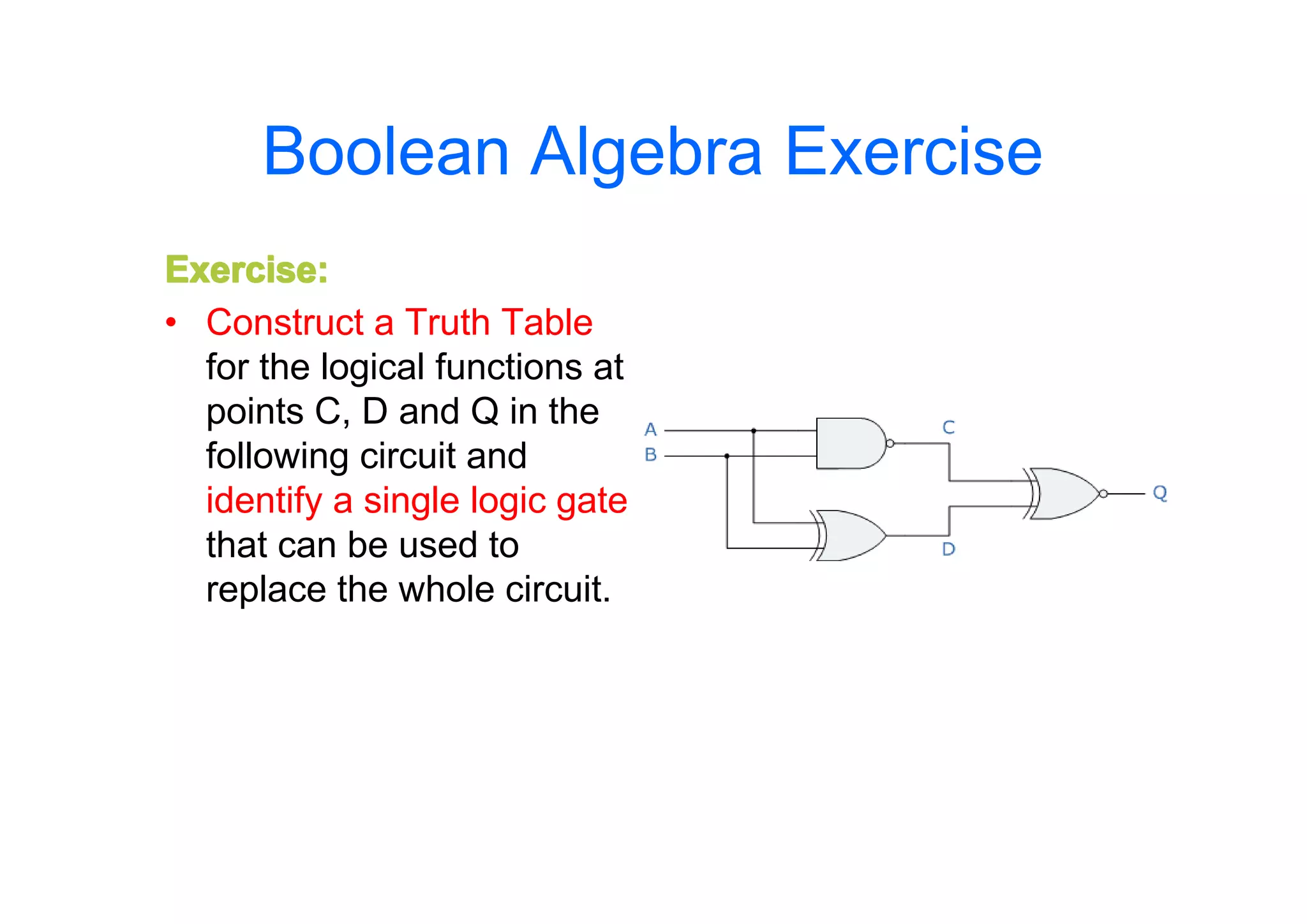
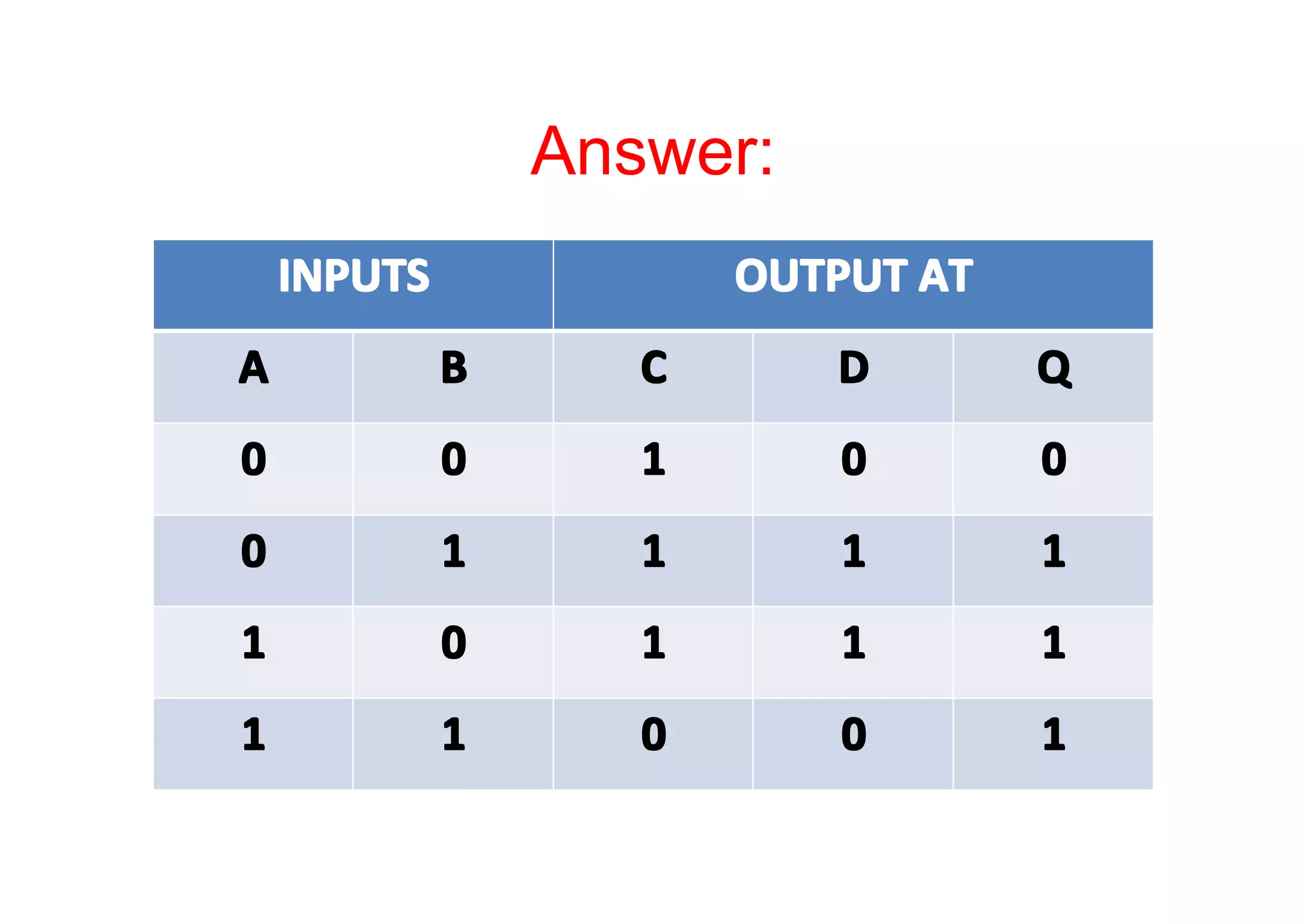
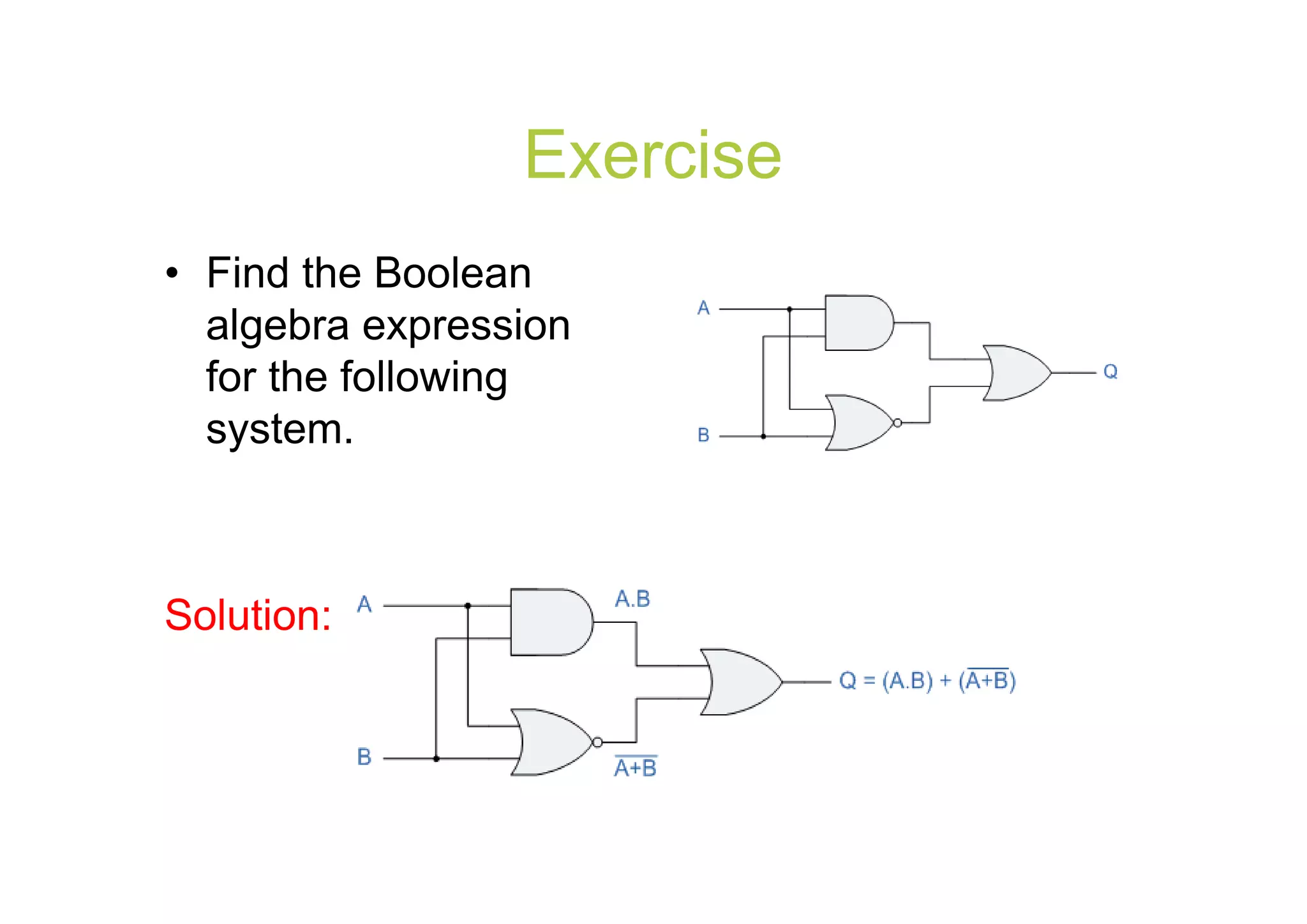
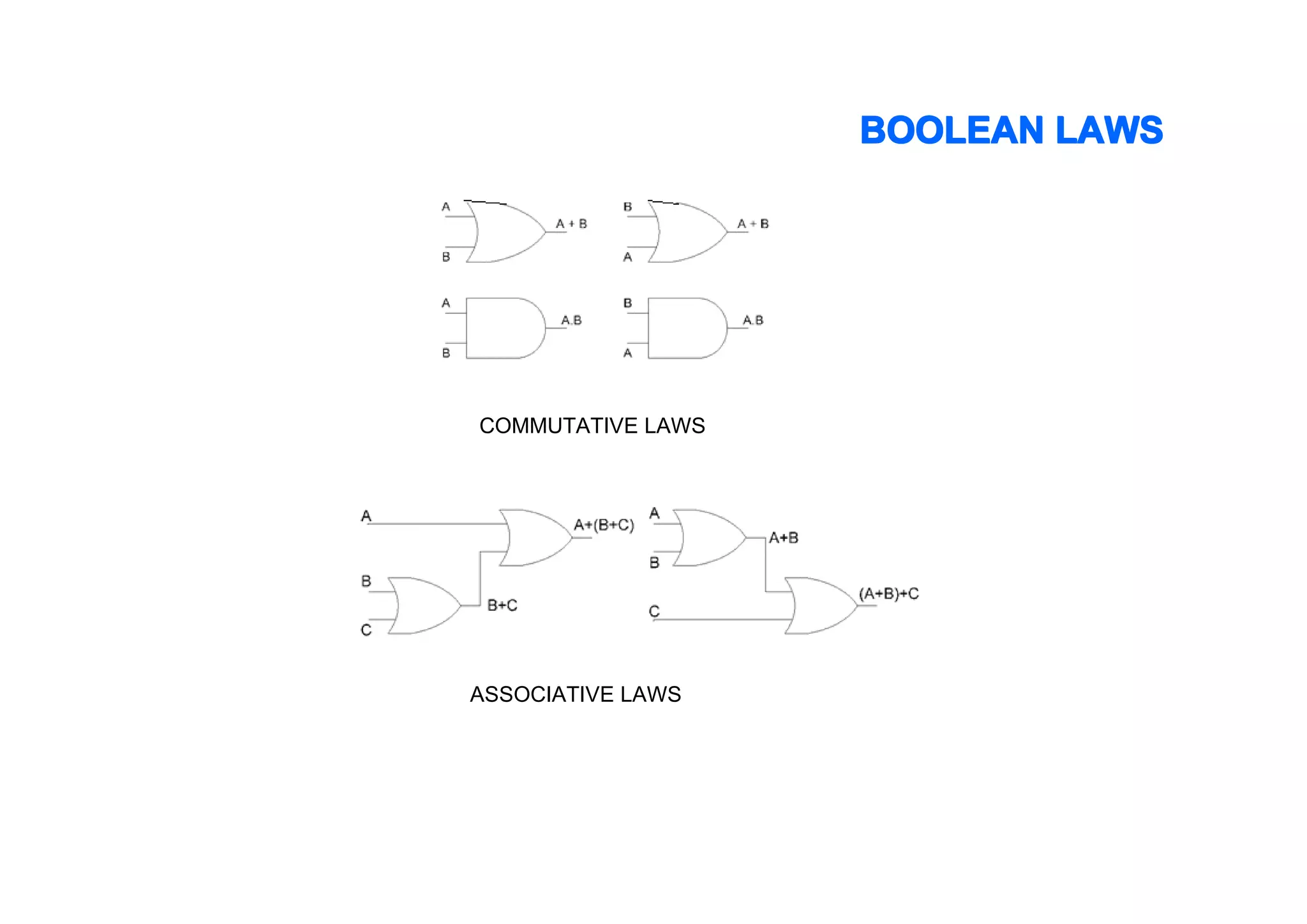
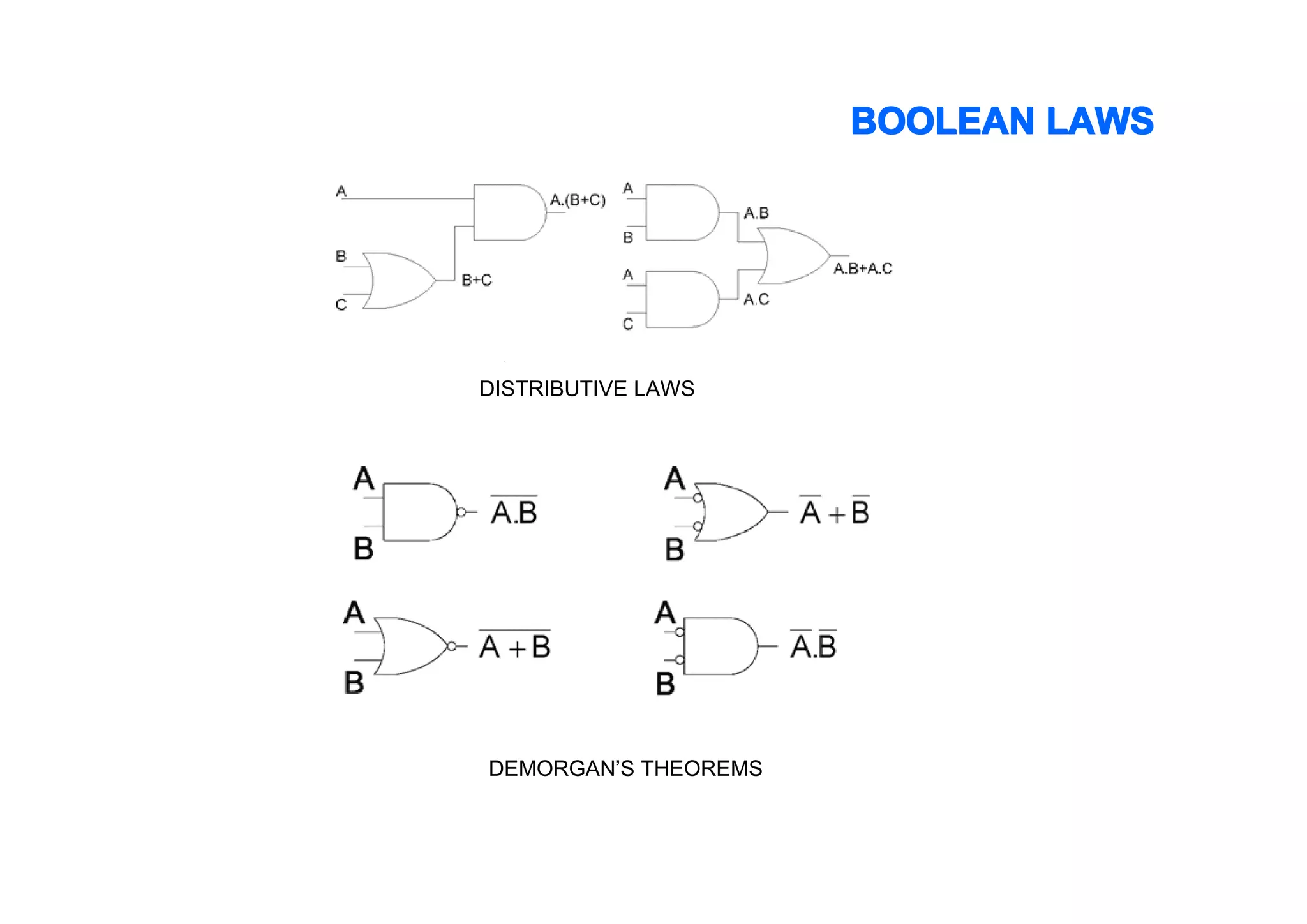
This document summarizes key topics from Chapter 2 of the course EE 202 Digital Electronics. It introduces Boolean operations including logic gates, truth tables, Boolean algebra, and Boolean laws. Logic gates such as AND, OR, NAND, and NOR are explained with their symbols, timing diagrams, and truth tables. Boolean algebra represents logical functions using variables and the operations of AND, OR, and NOT. Boolean laws like commutative, associative, distributive, and DeMorgan's theorems are presented to simplify logical expressions. Examples are provided to demonstrate applying these concepts to analyze and design combinational logic circuits.

1. EE 202 : DIGITAL ELECTRONICS
CHAPTER 2 : BOOLEAN
OPERATIONS
by : Siti Sabariah Salihin
Electrical Engineering Department
sabariah@psa.edu.my

2. CHAPTER 2 : BOOLEAN OPERATIONS
EE 202 : DIGITAL ELECTRONICS
Programme Learning Outcomes, PLO
Upon completion of the programme, graduates should be able to:
•
PLO 1 : Apply knowledge of mathematics, scince and engineering
fundamentals to well defined electrical and electronic engineering
procedures and practices
Course Learning Outcomes, CLO
• CLO 1 : Illustrate the knowledge of digital number systems,codes
and ligic operations correctly
• CLO 2 : Simplify and design combinational and sequential logic
circuits by using the Boolean Algebra and the Karnaugh Maps.
EE 202 : DIGITAL ELECTRONICS

3. Upon completion of this Topic 2
student should be able to:
2.1 Know the symbols,operations and functions of logic gates.
2.1.1 Draw the symbols, operations and
functions of logic gates.
2.1.2 Explain the Function of Logic gates using Truth
Table.
2.1.3 Construct AND, OR and NOT gates using only
NAND gates.
2.2
2.2.1
2.2.2
2.2.3
2.2.4
Know the basic concepts of Boolean Algebra and use them in
Logic circuits analysis and design.
Construct the basic concepts of Boolean Algebra
and use them in logic circuits analysis and design.
State the Boolean Laws.
Develop logic expressions from the truth table from
the form of SOP and POS
Simplify combinatinal Logic circuits using Boolean
Laws and Karnaugh Map
EE 202 : DIGITAL ELECTRONICS

4. TRUTH TABLES
�A truth table is a table that describes
the behavior of a logic gate
�The number of input combinations will
equal 2N for an N-input truth table
EE 202 : DIGITAL ELECTRONICS
4

5. LOGIC GATES
• Circuits which perform logic
functions are called gates
• The basic gates are:
I. NOT/INVERTER gate
II. AND gate
III. OR gate
IV. NAND gate
V. NOR gate
VI. XOR gate
VII. XNOR gate
EE 202 : DIGITAL ELECTRONICS

6. Symbol
I. NOT / INVERTER
Gate
Timing Diagram
Truth Table

7. II. AND Gate
Symbol
Timing Diagram
Truth Table

8. Symbol
III. OR gate
Timing Diagram
Truth Table

9. Symbol
IV. NAND Gate
Truth Table
Timing Diagram

10. V. NOR Gate
Symbol
Truth Table
Timing Diagram

11. VI. XOR Gate
Symbol
Truth Table
Timing Diagram

12. VII. XNOR Gate
Symbol
Truth Table
Timing Diagram

14. BOOLEAN ALGEBRA
• The Boolean algebra is an algebra dealing
with binary variables and logic operation
• The variables are designated by:
I. Letters of the alphabet
II. Three basic logic operations AND,
OR and NOT

15. BOOLEAN ALGEBRA
• A Boolean function can be represented by using
truth table. A truth table for a function is a list of
all combinations of 1’s and 0’s that can be
assigned to the binary variable and a list that
shows the value of the function for each binary
combination
• A Boolean expression also can be transformed
into a circuit diagram composed of logic gates
that implements the function

16. • Examples
F = A + BC
Truth Table
Logic circuit

17. Boolean Algebra Exercise
Exercise:
• Construct a Truth Table
for the logical functions at
points C, D and Q in the
following circuit and
identify a single logic gate
that can be used to
replace the whole circuit.

18. Solution
INPUTS
A
OUTPUT AT
B
C
D
Q

19. Answer:
INPUTS
OUTPUT AT
A
B
C
D
Q
0
0
1
0
0
0
1
1
1
1
1
0
1
1
1
1
1
0
0
1

20. Exercise
• Find the Boolean
algebra expression
for the following
system.
Solution:

21. BASIC IDENTITIES AND BOOLEAN
LAWS

22. BOOLEAN LAWS
COMMUTATIVE LAWS
ASSOCIATIVE LAWS

23. BOOLEAN LAWS
DISTRIBUTIVE LAWS
DEMORGAN’S THEOREMS

24. • All these Boolean basic identities and Boolean Laws
can be useful in simplifying a logic expression, in
reducing the number of terms in the expression
• The reduced expression will produce a circuit that is
less complex than the one that original expression
would have produced.
• Examples
Simplify this function
F=ABC+ABC+AC

25. Solution
CHAPTER 2 : EE202 DIGITAL ELECTRONICS

26. Exercise:
Using the Boolean laws, simplify the following expression:
Q= (A + B)(A + C)
Solution:
Q = (A + B)(A + C)
Q = AA + AC + AB + BC
Q = A + AC + AB + BC
Q = A(1 + C) + AB + BC
Q = A.1 + AB + BC
Q = A(1 + B) + BC
Q = A.1 + BC
Q = A + BC
( Distributive law )
( Identity AND law (A.A = A) )
( Distributive law
( Identity OR law (1 + C = 1)
( Distributive law )
( Identity OR law (1 + B = 1) )
( Identity AND law (A.1 = A) )
Then the expression: Q= (A + B)(A + C)
can be simplified to Q= A + BC
CHAPTER 2 : EE202 DIGITAL ELECTRONICS

27. continue chapter 2 Part B
REFERENCES:
1. "Digital Systems Principles And Application"
Sixth Editon, Ronald J. Tocci.
2. "Digital Systems Fundamentals"
P.W Chandana Prasad, Lau Siong Hoe,
Dr. Ashutosh Kumar Singh, Muhammad Suryanata.
Download Tutorials Chapter 2: Boolean Operations
@ CIDOS
http://www.cidos.edu.my