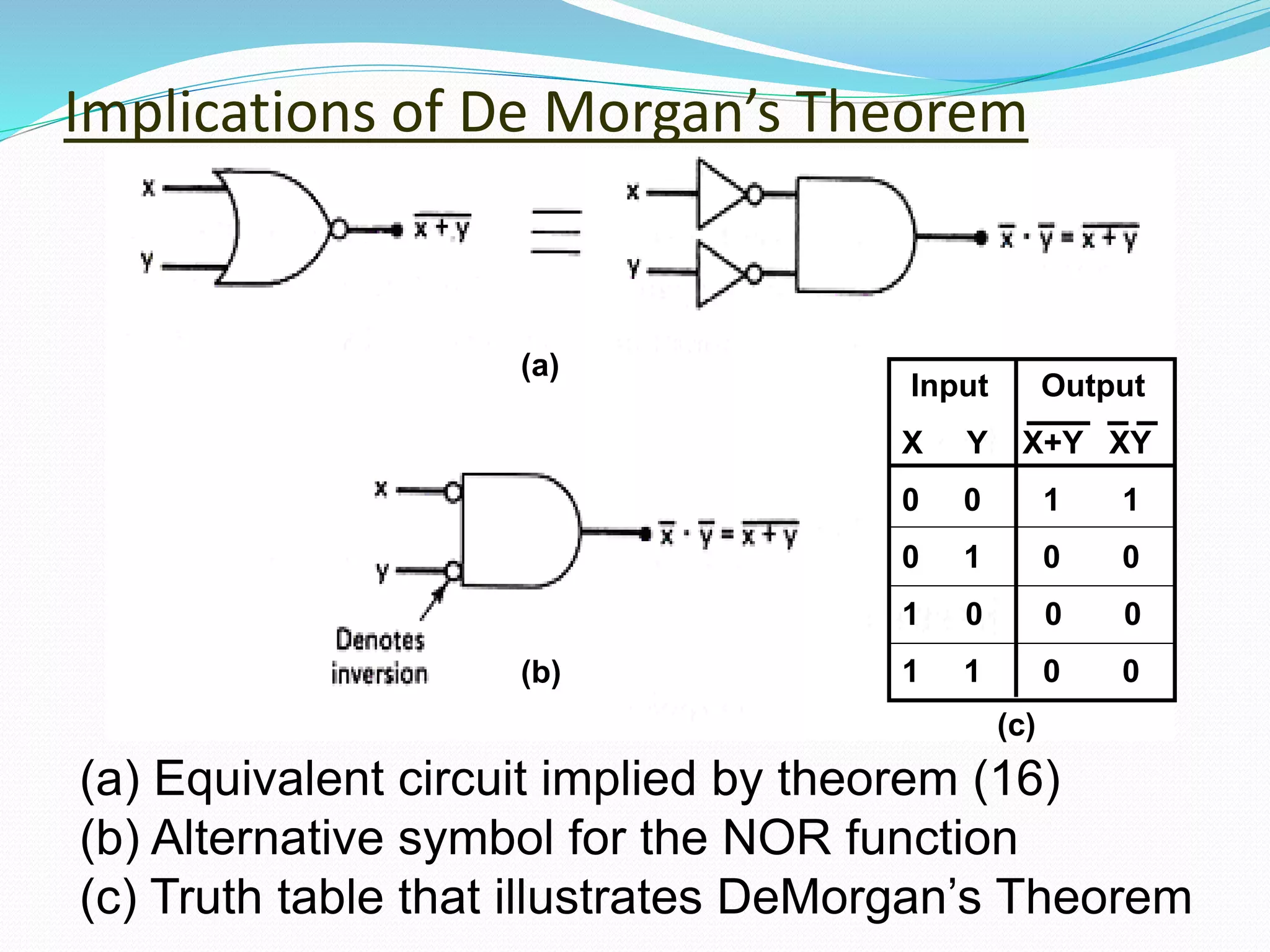
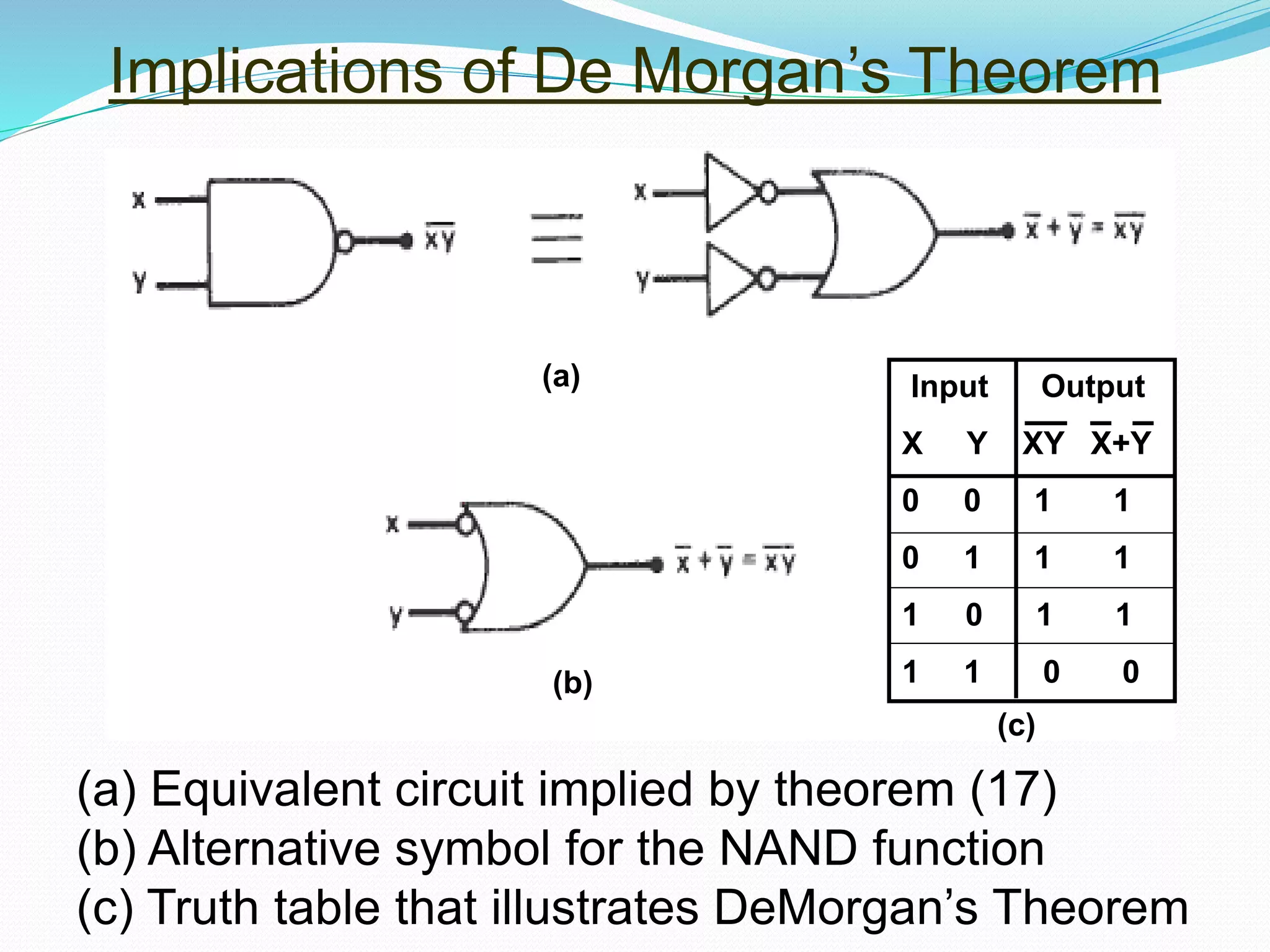
This document discusses Boolean logic and logic gates. It describes the basic logic gates - NOT, AND, and OR - and how more complex gates like NAND and NOR are derived from them. It also covers Boolean logic concepts like duality, De Morgan's theorems, and how logic gates can be combined into circuits to perform decision making and memory functions. Applications of logic gates include systems for genetic engineering, nanotechnology, industrial processes and medicine.