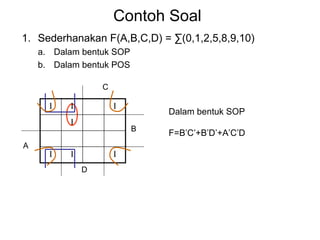
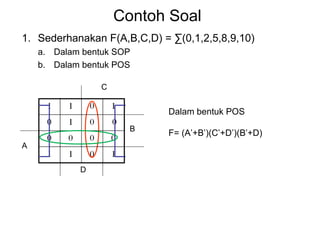
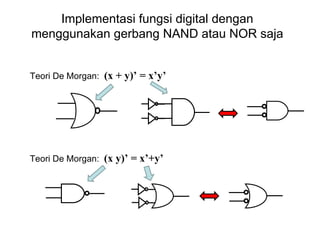
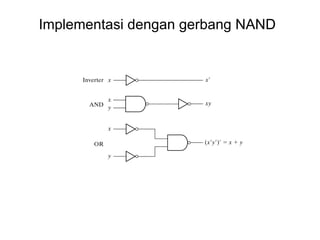
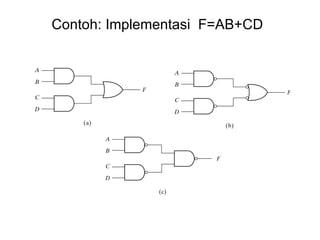
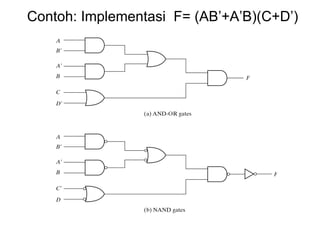
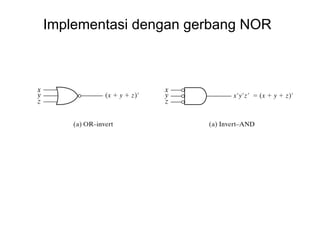
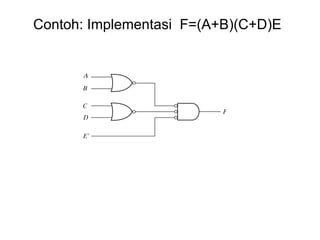
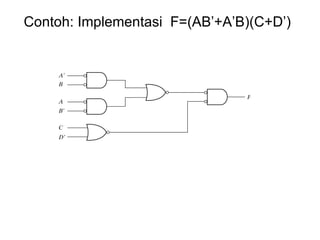
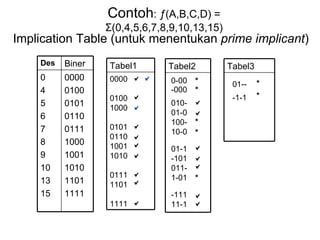
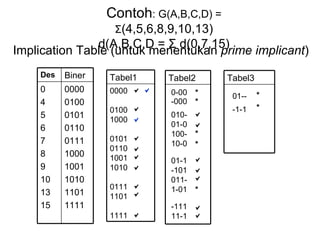
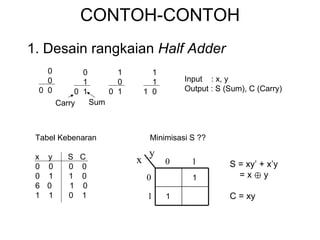
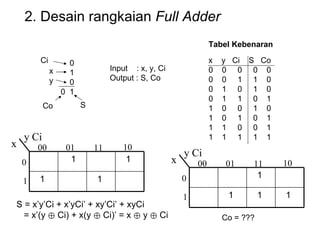
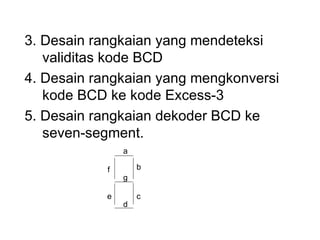
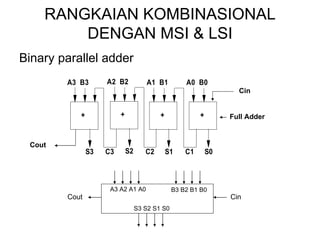
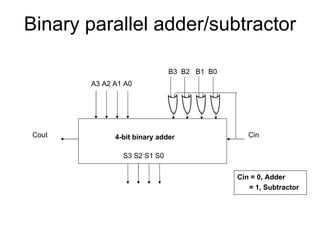
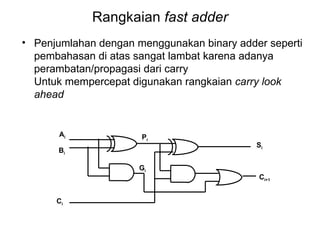
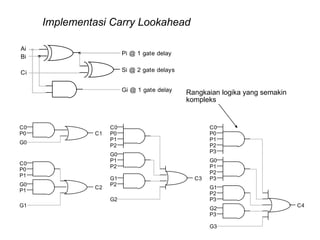
Dokumen tersebut memberikan contoh soal sederhanakan fungsi Boolean menggunakan beberapa metode seperti SOP, POS, peta-K, dan Quine-McCluskey. Selanjutnya menjelaskan implementasi fungsi digital menggunakan gerbang NAND dan NOR, serta metode desain rangkaian digital menggunakan komponen kombinasional seperti adder, dekoder, dan konverter kode.

1. Contoh Soal Sederhanakan F(A,B,C,D) = ∑(0,1,2,5,8,9,10) Dalam bentuk SOP Dalam bentuk POS Dalam bentuk SOP F=B’C’+B’D’+A’C’D A C B D

2. Contoh Soal Sederhanakan F(A,B,C,D) = ∑(0,1,2,5,8,9,10) Dalam bentuk SOP Dalam bentuk POS Dalam bentuk POS F= (A’+B’)(C’+D’)(B’+D) A C B D

3. Contoh Soal 2. Sederhanakan fungsi berikut dengan menggunakan Peta-K : F(A,B,C,D) = ∑(0,2,3,5,8,10,11) d(A,B,C,D) = ∑(1,7,9,12) Catatan: d(..) adalah don’t care bisa dianggap 0 atau 1 Tanpa don’t care: F= B’C + B’D’ + A’BC’D Dengan don’t care: F= B’ + A’D A C B D 1 d 1 1 1 d d 1 d 1 1

4. Implementasi fungsi digital dengan menggunakan gerbang NAND atau NOR saja Teori De Morgan: (x + y)’ = x’y’ Teori De Morgan: (x y)’ = x’+y’

5. Implementasi dengan gerbang NAND

6. Contoh: Implementasi F=AB+CD

7. Contoh: Implementasi F= (AB’+A’B)(C+D’)

8. Implementasi dengan gerbang NOR

9. Contoh: Implementasi F=(A+B)(C+D)E

10. Contoh: Implementasi F=(AB’+A’B)(C+D’)

11. Metode Quine-McCluskey (Tabular) Proses dua langkah: Menentukan prime implicants Menentukan minimal cover Semua proses dilakukan dengan menggunakan tabel Implicant yang berdekatan digabung, sebagai contoh: 0100 & 1100 menghasilkan -100 -100 & -101 menghasilkan -10-

12. Contoh : ƒ(A,B,C,D) = Σ(0,4,5,6,7,8,9,10,13,15) 0-00 010- 01-0 100- 10-0 01-1 -101 011- 1-01 -111 11-1 -000     *            01-- -1-1    * * * * * * Implication Table (untuk menentukan prime implicant ) Des Biner 0 4 5 6 7 8 9 10 13 15 0000 0100 0101 0110 0111 1000 1001 1010 1101 1111 Tabel1 0000 0100 1000 0101 0110 1001 1010 0111 1101 1111 Tabel2 Tabel3

13. Coverage Table (untuk mencari minimal cover ) 0,4(0-00) 0,8(-000) 8,9(100-) 8,10(10-0) 9,13(1-01) 4,5,6,7(01--) 5,7,13,15(-1-1) 0 X X 4 X X 5 X X 6 X 7 X X 8 X X X 9 X X Atau ƒ(A,B,C,D) = A’B + BD + AB’D’ + ??? + ??? 10 X 13 X X 15 X           ƒ(A,B,C,D) = A’B + BD + AB’D’ + AC’D + B’C’D’

14. Contoh : G(A,B,C,D) = Σ (4,5,6,8,9,10,13) d(A,B,C,D = Σ d(0,7,15) 0-00 010- 01-0 100- 10-0 01-1 -101 011- 1-01 -111 11-1 -000     *            01-- -1-1    * * * * * * Implication Table (untuk menentukan prime implicant ) Des Biner 0 4 5 6 7 8 9 10 13 15 0000 0100 0101 0110 0111 1000 1001 1010 1101 1111 Tabel1 0000 0100 1000 0101 0110 1001 1010 0111 1101 1111 Tabel2 Tabel3

15. Coverage Table (untuk mencari minimal cover ) 0,4(0-00) 0,8(-000) 8,9(100-) 8,10(10-0) 9,13(1-01) 4,5,6,7(01--) 5,7,13,15(-1-1) 4 X X 5 X X 6 X 8 X X X 9 X X 10 X 13 X X        ƒ(A,B,C,D) = A’B + AB’D’ + AC’D

16. Soal Latihan Sederhanakan fungsi berikut dengan menggunakan metode Quin-McCluskey: F(A,B,C,D) = ∑(0,2,3,5,8,10,11) d(A,B,C,D) = ∑(1,7,9)

17. SINTESIS (PERANCANGAN) RANGKAIAN DIGITAL Prosedur : Pahami persoalannya dengan benar Identifikasi input & outputnya Tuliskan tabel kebenarannya Sederhanakan fungsinya Gambarkan rangkaiannya

18. CONTOH-CONTOH 1. Desain rangkaian Half Adder Input : x, y Output : S (Sum), C (Carry) S = xy’ + x’y = x ⊕ y C = xy 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 0 Carry Sum Tabel Kebenaran x y S C 0 0 0 0 0 1 1 0 0 1 0 1 1 0 1 1 1 x y 0 0 1 1 Minimisasi S ??

19. 2. Desain rangkaian Full Adder Input : x, y, Ci Output : S, Co S = x’y’Ci + x’yCi’ + xy’Ci’ + xyCi = x’(y ⊕ Ci) + x(y ⊕ Ci)’ = x ⊕ y ⊕ Ci Co = ??? Co S 0 1 0 0 1 x y Ci Tabel Kebenaran x y Ci S Co 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 x y Ci 0 1 00 01 11 10 1 1 1 1 x y Ci 0 1 00 01 11 10

20. 3. Desain rangkaian yang mendeteksi validitas kode BCD 4. Desain rangkaian yang mengkonversi kode BCD ke kode Excess-3 5. Desain rangkaian dekoder BCD ke seven-segment. b g a c d e f

21. RANGKAIAN KOMBINASIONAL DENGAN MSI & LSI Binary parallel adder Full Adder Cout Cin A3 A2 A1 A0 B3 B2 B1 B0 S3 S2 S1 S0 Cin Cout

22. Binary parallel adder/subtractor A3 A2 A1 A0 B3 B2 B1 B0 S3 S2 S1 S0 Cin Cout Cin = 0, Adder = 1, Subtractor 4-bit binary adder

23. Rangkaian konverter dari BCD ke Excess-3 dengan menggunakan 4 bit adder Cout Cin Input BCD 1 0 Output: Kode Excess-3 A0 A1 A2 A3 B0 B1 B2 B3 S0 S1 S2 S3

24. Rangkaian fast adder Penjumlahan dengan menggunakan binary adder seperti pembahasan di atas sangat lambat karena adanya perambatan/propagasi dari carry Untuk mempercepat digunakan rangkaian carry look ahead S i C i+1 B i A i C i P i G i

25. Rangkaian fast adder Dari rangkaian fast adder, bila: P i = A i ⊕ B i (carry propagate) G i = A i B i (carry generate) Maka: S i = P i ⊕ C i C i+1 = G i + P i C i Bila C 0 diketahui, maka C 1 , C 2 dst dapat dicari sbb: C 1 = G 0 + P 0 C 0 C 2 = G 1 + P 1 C 1 = G 1 + P 1 (G 0 + P 0 C 0 ) = G 1 + P 1 G 0 + P 1 P 0 C 0 C 3 = G 2 + P 2 C 2 = G 2 + P 2 (G 1 + P 1 G 0 + P 1 P 0 C 0 ) = G 2 + P 2 G 1 + P 2 P 1 G 0 + P 2 P 1 P 0 C 0 C 4 = G 3 + P 3 C 3 = ???

26. Implementasi Carry Lookahead Rangkaian logika yang semakin kompleks