Heap sort uses a heap data structure that maintains the max-heap or min-heap property. It involves two main steps: 1) building the heap from the input array using the BUILD-MAX-HEAP procedure in O(n) time, and 2) repeatedly extracting the maximum/minimum element from the heap and inserting it into the sorted portion using the DELHEAP procedure, running in O(n log n) time overall. The key operation is MAX-HEAPIFY, which maintains the max-heap property in O(log n) time during heap operations like insertion and deletion.

1. HEAP SORT

2. Heap tree is a complete binary tree but
at lowest level of it is not necessary to
make heap tree a complete binary tree.
complete binary tree
Not necessray
Heap Sort

3. Heap Sort
•:Length: Number of elements in the
array
•Heap-size - how many elements in the
heap are stored within
array A.

4. Tree (Binary tree)
Arrays
TWO WAYS TO IMPLEMENT
HEAP-SORT:

5.  Maintaining heap property (min
or max)
 Maintaining shape property
(complete binary tree)
STEPS TO BUILD HEAP

6. MAINTAINING HEAP PROPERTY

7. Each node in a tree has a key which is
more extreme (greater or less) than or
equal to the key of its parent.
 A complete tree with the heap property is
a heap.

8. MAX-HEAP PROPERTY
Each node in a tree has a key which is
less than or equal to the key of its parent.
A[PARENTi] >= A[i]
“While using this property it makes a list of
descending order.”

9. MIN-HEAP PROPERTY
Each node in a tree has a key which is
greater than or equal to the key of
its parent.
A[PARENTi] <= A[i]
“While using this property it makes a list of
ascending order.”

10. OPERATIONS ON HEAP
 Inserting an element with an
arbitrary key
 Deletion of largest key

11. INSERTION
 Add the element to the bottom level of the
heap.
 Compare the added element with its parent;
if they are in the correct order, stop.
 If not, swap the element with its parent and
return to the previous step.

12. DELETION
 Replace the root of the heap with the last element
on the last level.
 Compare the new root with its children; if they are
in the correct order, stop.
 If not, swap the element with one of its children
and return to the previous step. (Swap with its
smaller child in a min-heap and its larger child in a
max-heap.)

13. BUILD HEAP

14. BUILDING THE HEAP
“ The Build heap method
shown in Program transforms an
unsorted array into a max heap or
min heap ”

15. “
”
BUILD-MAX-HEAP(A,i)
1 A:heap-size = A[length]
2 for i = A[length/2] down to 1
3 MAX-HEAPIFY(A,I )
• Each call to MAX-HEAPIFY costs O.lg n/ time.
BUILDMAX-HEAP makes O.n/ such calls. Thus, the
running time is O.n lg n/. This upper bound, though
correct, is not asymptotically tight.
Algorithm

16. EXAMPLE (MAX-HEAP & LEFT ALIGNED)

17. 15
10
177
19
16
0 1 2 3 4 5

18. 15
10
177
19
16
7
16
15
177
19
10
7

19. 16
15
177
19
10
7
16
15
177
19
10
7

20. 16
15
177
19
10
7
16
19
177
15
10
7

21. 16
19
157
17
10
7

22. The heapsort algorithm

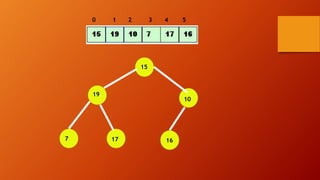
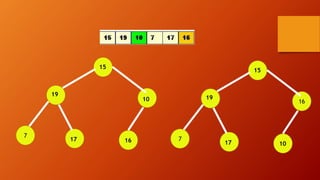
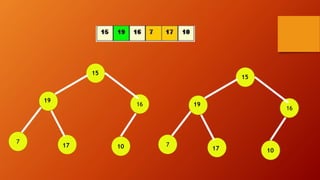
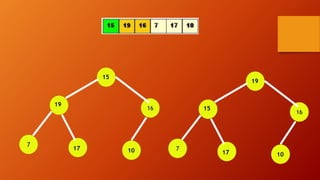
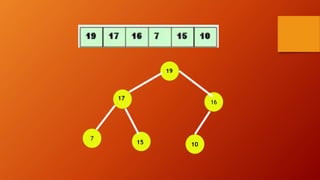
23. INSHEAP(TREE, N, ITEM)
Heap H with N elements is stored in the array
Tree, and an ITEM of information is given. This
procedure inserts ITEM as a new element of H.
PTR gives the location of ITEM as it rise in the
tree, and PAR denotes the location of parents of
ITEM.
1. [Add new node to H and initialize PTR]
Set N := N+1 and PTR := N
2. [Find location to insert ITEM]
Repeat steps 3 to 6 while PTR < 1

24. 3. Set PAR := [PTR/2]. [Location of parent
node]
4. If ITEM <= TREE[PAR], then:
Set TREE[PTR] := ITEM, and Return.
[END of IF structure]
5. Set TREE[PTR] := TREE[PAR]. [Moves node
down]
6. Set PTR := PAR. [Updates PTR].
[End of step 2 loop]
7. [Assign ITEM as the root of H.]
8. Set TREE[1] := ITEM.
9. Return.

25. DELHEAP(TREE, N, ITEM)
A Heap H with N elements is stored in the array
TREE. This procedure assigns the root TREE[1] of H
to the variable ITEM and then reheaps the remaining
elements. The variables LAST saves the value of the
original Last node of H. The pointers PTR, LEFT and
RIGHT give the locations of LAST and its left and
right children as LAST sinks in the tree.
1. Set ITEM := TREE[1]. [Removes root of H.]
2. Set LAST := TREE[N] and N := N-1
[Removes last node of H.]

26. 3. Set PTR := 1, LEFT := 2
and RIGHT := 3. [Initializes pointers.]
4. Repeat Steps 5 to 7 while RIGHT <= N:
5. If LAST >= TREE[LEFT] and
LAST >= TREE[RIGHT], then:
Set TREE[PTR] := LAST and Return.
[End of IF Structure.]
6. If TREE[RIGHT] <= TREE[LEFT], then:
Set TREE[PTR] := TREE[LEFT] and
PTR := LEFT.
Else:
Set TREE[PTR] := TREE[RIGHT] and
PTR := RIGHT.
[End of IF structure.]

27. 7. Set LEFT := 2 * PTR and
RIGHT := LEFT+1.
[End of Step 4 loop.]
8. If LEFT = N and
If LAST < TREE[LEFT], then:
Set PTR := LEFT.
9. Set TREE[PTR] := LAST.
10. Return.

28. HEAPSORT(A, N)
An array A with N elements is given. This algorithm sorts the
elements of A.
1. [Build a Heap H, using Procedure INSHEAP(TREE, N, ITEM) ]
Repeat for J = 1 to N-1:
Call INSHEAP(A, J, A[J+1]).
[End of loop]
2. [Sort A by repeatedly deleting the root of H, using procedure
DELHEAP(TREE, N, ITEM) ]
Repeat while N > 1:
(a) Call DELHEAP(A, N, ITEM).
(b) Set A[N+1] := ITEM.
[End of loop.]
3. Exit.

29. About Heap
MAX-HEAPIFY procedure
O(lg n) time, is
the key to
maintaining
the max-heap
property.
BUILD-MAX-HEAP procedure
Runs in linear
time, produces
a maxheap
from an
unordered
input array.
HEAPSORT procedure
O(n lg n) time,
sorts an array
in place.