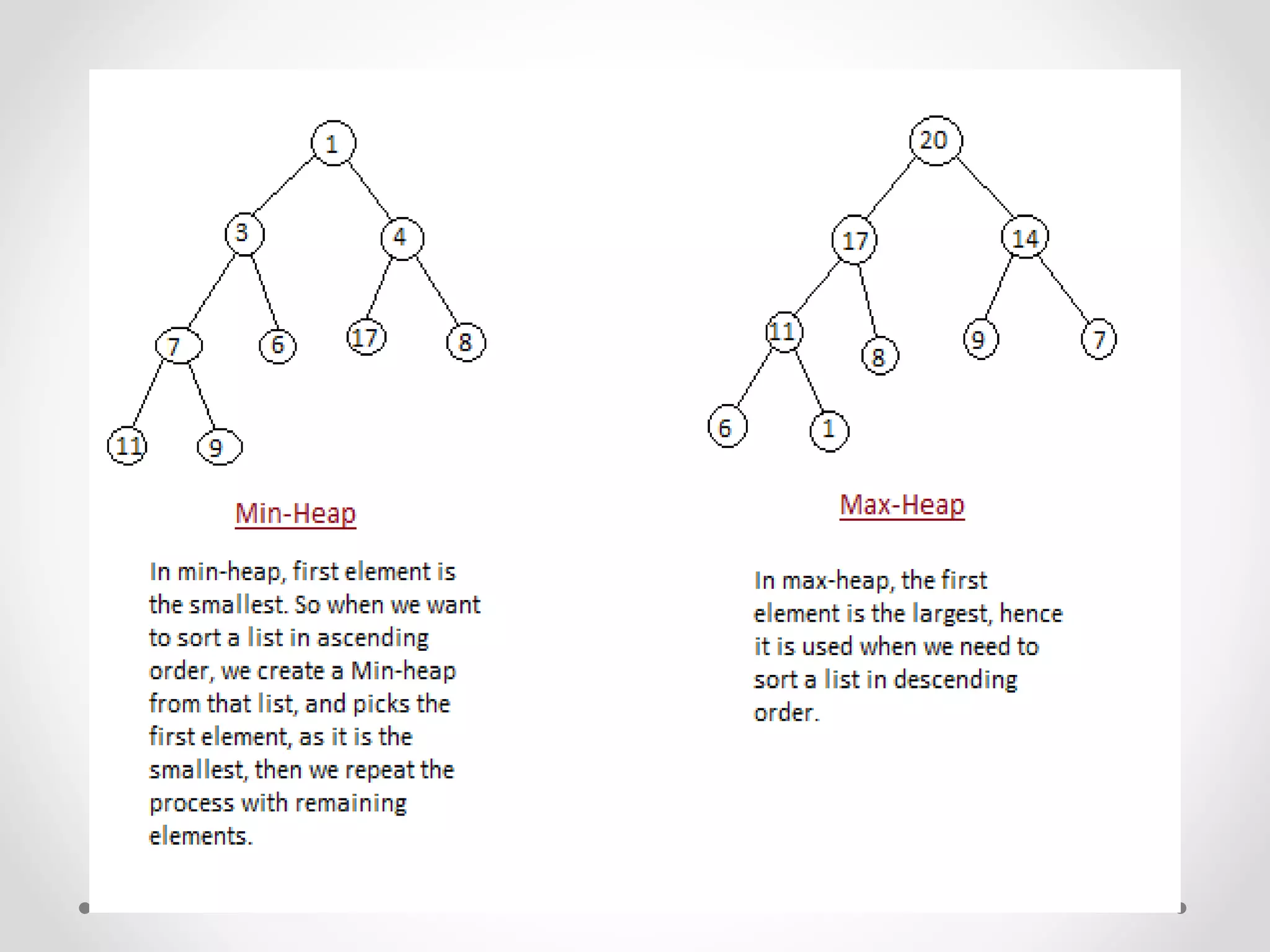
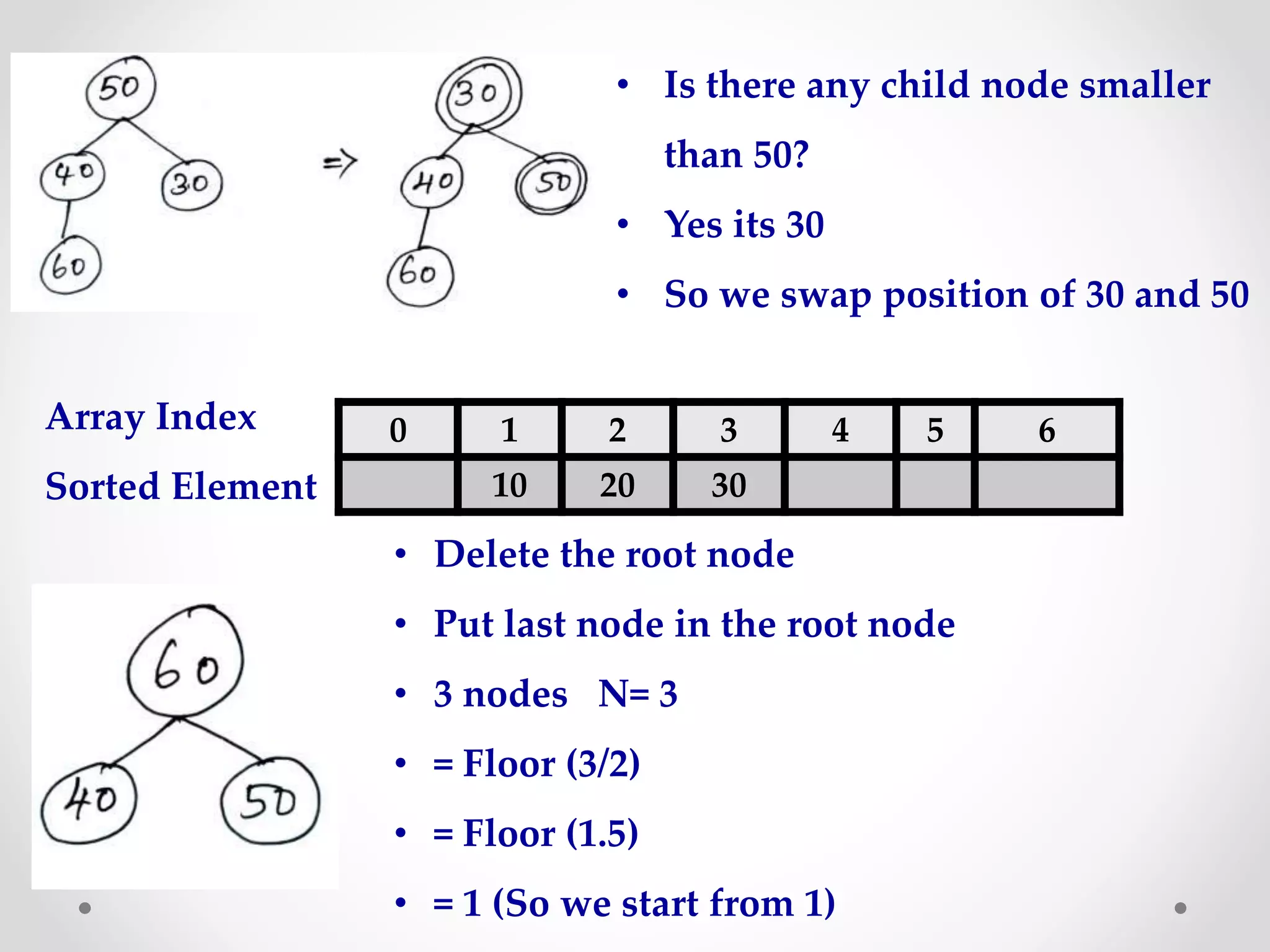
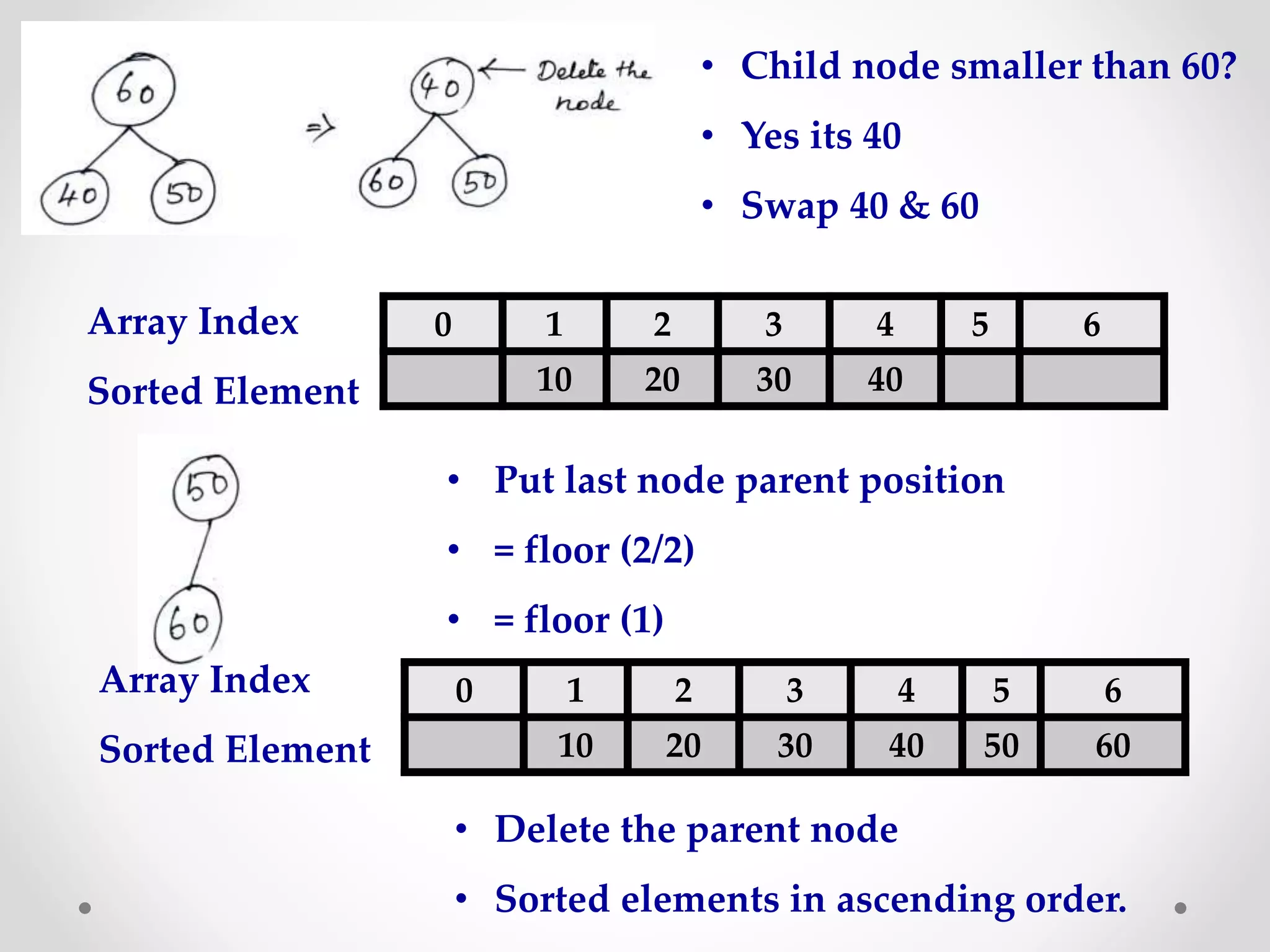
Heap sort is a sorting algorithm that uses a heap data structure. It first builds a max or min heap from the input elements. For ascending order, it builds a min heap where each parent node is smaller than its children. It then repeatedly removes the root node and replaces it with the last element, maintaining the heap property. This process continues until all elements are sorted. The time complexity of heap sort is O(n log n) as building and maintaining the heap takes O(log n) for each of the n elements.

1. Data Structures and Algorithm

2. Prepared by
Mrs.P.Anusha M.Sc(IT).,M.Phil.,D.P.T.T.,(Ph.D).,
Assistant professor,
Department of Information Technology,
Bon secours college for women,
Thanjavur.

3. HEAP SORT

4. Heap Sort
• Heap - A max (min)heap is a complete binary tree with the
property that the value at each node is at least as large as (as
small as) the values at its children(if they exist). Call this
property the heap property.
Shape Property: Heap data structure is always a Complete
Binary Tree, which means all levels of the tree are fully filled.
Heap Property: All nodes are either greater than or equal
to or less than or equal to each of its children. If the parent
nodes are greater than their child nodes, heap is called a Max-
Heap, and if the parent nodes are smaller than their child
nodes, heap is called Min-Heap.

6. • In this sorting algorithm we first build a heap using given
elements.
• If we want to sort the elements in ascending order we create
a Min Heap.
• And to sort the elements in descending order we create a
Max Heap

7. • Once the heap is created we delete the root node from the
heap and put the last node in the root position and repeat
the steps till we have covered all elements.
Example: Sorting in Ascending Order
1. Build Heap
2. Transform the heap into min heap
3. Delete the root node
4. Put the last node of the heap in root position
5. Repeat from step 2 till all nodes are covered.

8. 40 60 10 20 50 30
Input
• There are 6 elements. So our heap will have 6 nodes.
• We can represent the nodes of the heap in an array.
0 1 2 3 4 5 6
40 60 10 20 50 30
Array Index
Input
• Array Index starts from 0
• We can save the elements from index 1.

9. Build Heap
Create a Min Heap
Here 6 nodes
N = 6
Floor(N/2)
= floor(6/2)
= floor (3)
= 3
=> We start comparison from 3
• Min Heap the parent
node is always smaller
than or equal to its child
nodes.

10. • Is there any child node smaller than 60?
• Yes its 20
• So we swap position of 20 and 60
• Is there any child node smaller than 10?
No
• So we move to index 2 or the 2nd node.
• We move to index 1 of the 1st node
• Is there any child node smaller than 40?
• Yes, its 10
• So we swap 10 & 40
• Min Heap – a parent node is always smaller
than or equal to child nodes.

11. • Delete the root node
• Now we will take the element at the root
node and put it in our sorted element list
• So we have a min heap.
• Put the last node in the root position.
• Now there are 5 nodes. N = 5
• = floor (N/2)
• = floor (5/2)
• = 2.5
• = 2 (Start from 2 node)
0 1 2 3 4 5 6
10
Array Index
Sorted Element

12. • Any child node smaller than 20?
• No.
• So we move to index 1 or the 1st node
See, parent node are smaller than child node
So we have a min heap
0 1 2 3 4 5 6
10 20
Array Index
Sorted Element

13. • Is there any child node smaller than 40?
No
• So we move to index 1st node.
• Put the last node in the root position.
• Now there are 4 nodes. N = 4
• = floor (N/2)
• = floor (4/2)
• = 2 (Start from 2 node)

14. • Is there any child node smaller
than 50?
• Yes its 30
• So we swap position of 30 and 50
• Delete the root node
• Put last node in the root node
• 3 nodes N= 3
• = Floor (3/2)
• = Floor (1.5)
• = 1 (So we start from 1)
0 1 2 3 4 5 6
10 20 30
Array Index
Sorted Element

15. • Put last node parent position
• = floor (2/2)
• = floor (1)
• Child node smaller than 60?
• Yes its 40
• Swap 40 & 60
• Delete the parent node
• Sorted elements in ascending order.
0 1 2 3 4 5 6
10 20 30 40
Array Index
Sorted Element
0 1 2 3 4 5 6
10 20 30 40 50 60
Array Index
Sorted Element