Heaps are nearly complete binary trees stored as arrays that satisfy the heap property: for max-heaps a parent node is greater than or equal to its children, and for min-heaps a parent is less than or equal to its children. Heap operations like insert, extract max/min, and increase/decrease key take O(log n) time due to the heap's height. The heapsort algorithm uses a max-heap to sort an array in O(n log n) time by repeatedly extracting and placing the max element in its final position. Priority queues implemented with heaps support insertion, maximum/minimum extraction, and key increases/decreases in O(log n) time.

1. Data Structures & Algorithms
Heapsort

2. Heaps
A heap is data
structure that can be
viewed as a nearly
complete binary tree
 Each node
corresponds to an
element of an array
that stores its
values
 The tree is
completely filled on
all levels except the
lowest
2 4 1
8 7 9 3
1414 10
16

3. Heaps
Heaps are typically stored using arrays
 The array is of size length(A)
 heapsize(A) elements are currently in use
 A[1] is the “root” node of the tree
 Any element x has the following properties:
 Parent(x) is x/2
 Left(x) is 2*x
 Right(x) is 2*x+1
16 14 10 8 7 9 3 2 4 1
1 2 3 4 5 6 7 8 9 10

4. The Heap Property
Heaps satisfy what is known as the heap
property:
 For a max-heap, the heap property is:
 A[Parent(x)] >= A[x]
 I.e., the root node of the tree or any subtree has a
larger value than any node in its subtrees
 This is reversed for min-heaps:
 A[Parent(x)] <= A[x]
 I.e., the smallest element is at the root

5. Terminology
Height of a node = number of edges
that must be traversed to get from that
node to a leaf
Height of a tree = height of the root =
O(lg n)
Basic heap operations generally take
O(lg n), because they are based on the
height of the tree

6. Maintaining the Heap Property
MaxHeapify is a routine used to maintain the
max-heap property of an array
 It takes as input the array to heapify, the element
to begin with, and the number of elements in the
heap
 Assumes Left(x) and Right(x) are heaps, but the
tree rooted at x may not be, thus violating the
heap property
 The idea is to propagate x through the tree into
it’s proper position

7. MaxHeapify
MaxHeapify(A, x, heapsize)
{
L = Left(x)
R = Right(x)
if ( L < heapsize && A[L] > A[x] )
Largest = L
else
Largest = x
if ( R <= heapsize && A[R] > A[Largest] )
Largest = R
if ( Largest != x )
{
swap(A[x], A[Largest])
MaxHeapify(A, Largest, heapsize)
}
}

8. MaxHeapify In Action
Here, the red node is out of place, violating
the heap property
2 8 1
14 7 9 3
144 10
16

9. MaxHeapify In Action
After calling MaxHeapify(A, 2, 10), the red
node is pushed further down the heap
2 8 1
4 7 9 3
1414 10
16

10. MaxHeapify In Action
After calling MaxHeapify(A, 4, 10), the heap is now
correct – a further call to MaxHeapify(A, 9, 10) will
yield no further changes
2 4 1
8 7 9 3
1414 10
16

11. Building a Heap
Given an unsorted array, we can build a
heap recursively from the bottom-up
using this algorithm:
BuildMaxHeap(A, size)
{
for ( x = length(A)/2 ; x >= 1 ; --x )
MaxHeapify(A, x, size)
}

12. Building a Heap
14 8 7
2 16 9 10
141 3
4
1
2 3
4 5 6 7
8 9 10

13. Building a Heap
14 8 7
2 16 9 10
141 3
4
1
2 3
4 5 6 7
8 9 10

14. Building a Heap
2 8 7
14 16 9 10
141 3
4
1
2 3
4 5 6 7
8 9 10

15. Building a Heap
2 8 7
14 16 9 3
141 10
4
1
2 3
4 5 6 7
8 9 10

16. Building a Heap
2 8 7
14 1 9 3
1416 10
4
1
2 3
4 5 6 7
8 9 10

17. Building a Heap
2 8 1
14 7 9 3
1414 10
16
1
2 3
4 5 6 7
8 9 10

18. Analysis of BuildMaxHeap
How long does it take?
 MaxHeapify has cost O(lgn), and is called O(n)
times, so intuitively there’s O(nlgn)
 This isn’t an asymptotically tight bound, though
 The MaxHeapify cost isn’t really based on n
 It’s cost is based on the height of the node in the tree
 An n-element heap has height lgn, and at most n/2h+1
nodes of any height h
 The math at this point gets a bit complicated, but
results in a running time of O(n) (see pg. 145
(old)/135 (new))

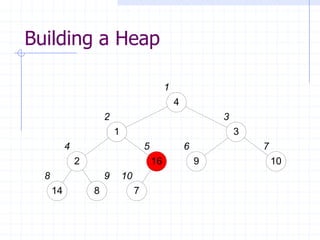
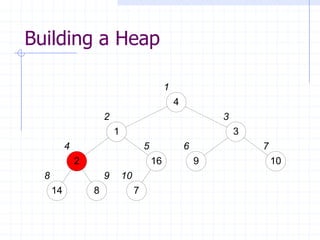
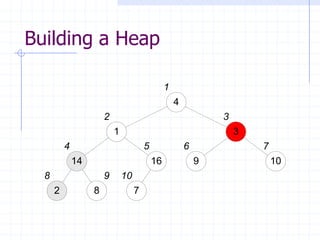
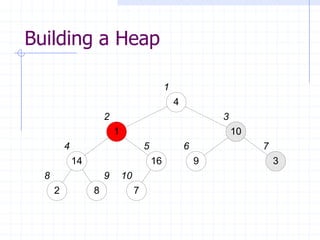
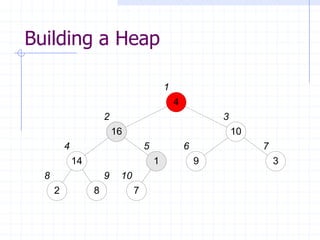
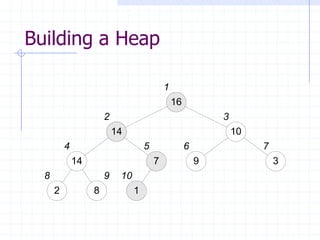
19. The HeapSort Algorithm
The HeapSort algorithm sorts an array by
using a max-heap as an intermediate
step
 First, a max-heap is built from the input
 The max element is exchanged with
A[heapsize], to put it in its final position
 The remainder of the array is then re-
heapified, using heapsize - 1

20. The HeapSort Algorithm
HeapSort(A, size)
{
BuildHeap(A, size)
For ( x = size ; x >= 2 ; --x )
{
swap(A[1], A[x])
--heapsize
Heapify(A, 1, x-1)
}
}
What is the running time of HeapSort?

21. Analysis of HeapSort
In practice, the HeapSort will usually be
beat by QuickSort
The heap data structure has a number of
other uses, however

22. Priority Queues
One use of a heap is as a priority queue
Priority queues are often used in an OS to
perform job/resource scheduling
 Also in simulators, and many other tasks
A priority queue is a data structure for
maintaining a set of elements (S), each with
an associated value called a key
 Priority queues come in two flavors: max-priority
queues and min-priority queues

23. Priority Queues
Max-priority queues support these
operations:
 Insert(S, x) – inserts x into S
 Maximum(S) – returns the element in S with the
largest key
 ExtractMax(S) – removes and returns the element
in S with the largest key
 IncreaseKey(S, x, k) – increases the value of
element x’s key to the new value k

24. Priority Queuess
HeapMaximum(A)
{
return A[1];
}

25. Priority Queues
HeapExtractMax(A, heapsize)
{
if ( heapsize < 1 )
throw HeapUnderflowError();
max = A[1];
A[1] = A[heapsize];
--heapsize;
MaxHeapify(A, 1, heapsize);
return max;
}

26. Priority Queues
HeapIncreaseKey(A, i, key)
{
if ( key < A[i] )
throw HeapKeyError();
A[i] = key;
while ( i > 1 && A[Parent(i) < A[i] )
{
swap(A[i], A[Parent(i)]);
i = Parent(i);
}
}

27. Priority Queues
MaxHeapInsert(A, key, heapsize)
{
++heapsize;
A[heapsize] = -MAXKEY;
HeapIncreaseKey(A, A[heapsize], key);
}

28. Exercises
1st Edition:
 Pg 142: 7.1-1, 7.1-2, 7.1-6
 Pg 144: 7.2-1, 7.2-2, 7.2-4
 Pg 150: 7.5-3, 7.5-5
2nd Edition
 Pg 129: 6.1-1, 6.1-2, 6.1-6
 Pg 132: 6.2-1, 6.2-3, 6.2-5
 Pg 142: 6.5-6, 6.5-7