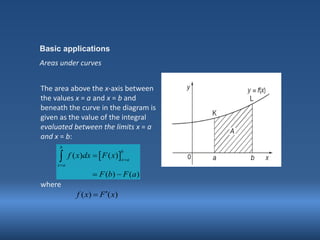
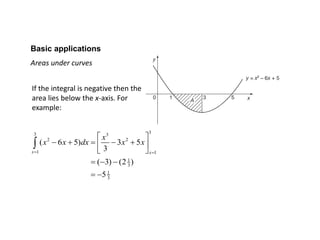
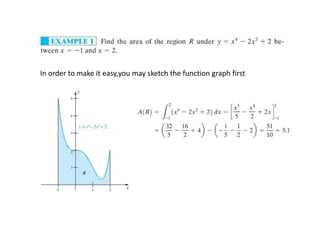
The document discusses the calculation of areas under curves using integrals, including both basic applications and examples of finding areas between curves. It also covers the volumes of solids of revolution using the methods of disks and washers, alongside examples for each method. Additionally, the document touches on applications of integrals in fields such as science and population growth.

1. Integration Application
THP-FTP-UB

2. Basic applications
Areas under curves
The area above the x-axis between
the values x = a and x = b and
beneath the curve in the diagram is
given as the value of the integral
evaluated between the limits x = a
and x = b:
where
 ( ) ( )
( ) ( )
b
b
x a
x a
f x dx F x
F b F a



 

( ) ( )f x F x

3. Basic applications
Areas under curves
If the integral is negative then the
area lies below the x-axis. For
example:
33 3
2 2
1 1
1
3
1
3
( 6 5) 3 5
3
( 3) (2 )
5
x x
x
x x dx x x
 
 
     
 
  
 


4. In order to make it easy,you may sketch the function graph first

6. The Area of The Region Between Two Curves
Example
Find the area of the region between the curves 𝑦 = 𝑥4
and 2𝑥 − 𝑥2.
Answer
Sketch the functions graph first, then finding where the
two curves intersect.
Try! Find the area of the region between 𝒚 𝟐
= 𝟒𝒙 and
4x – 3y = 4

7. The Area Bounded By the Curves in Form of
Parametric Equations
Example

8. Try!
Find the area of the
indicated region
A curve has parametric equations 𝑥 = 𝑐𝑜𝑠2
𝑡, 𝑦 = 3𝑠𝑖𝑛2
𝑡. Find the
area bounded by the curve, the x-axis and the ordinates at 𝑡 =
0 𝑎𝑛𝑑 𝑡 = 2𝜋

9. Volumes of Solid of Revolutions:
Method of Disks
Let 𝑉 be the volume of the solid generated.
Since the solid generated is a flat cylinder, so 𝑉 is:

12. We finally obtain:

13. Volumes of Solid of Revolutions:
Method of Washers
Sometimes, slicing a solid of revolution result in disks with hole in
the middle
Find the volume of the solid generated by revolving the region
bounded by the parabolas 𝑦 = 𝑥2 and 𝑦2 = 8𝑥 about the 𝑥 −axis

15. 15
Jika V(t) adl volume air dlm waduk pada waktu t, maka turunan V’(t) adl
laju mengalirnya air ke dalam waduk pada waktu t.
)V(t)V(tdt(t)V' 12
2t
1t

perubahan banyaknya air dalam waduk diantara t1 dan t2
Penerapan Integral dalam Ilmu Sains

16.  
2t
1t
dt
dt
d[C]
[C](t2)-[C](t1)
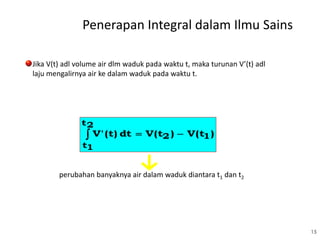
Jika [C](t) adl konsentrasi hasil suatu reaksi kimia
pd waktu t,maka laju reaksi adl turunan d[C]/dt
perubahan konsentrasi C dari waktu t1 ke t2

17. 17
Jika laju pertumbuhan populasi adl dn/dt, maka
)n(t)n(tdt
dt
dn
12
2t
1t

pertambahan populasi selama periode waktu t1 ke t2