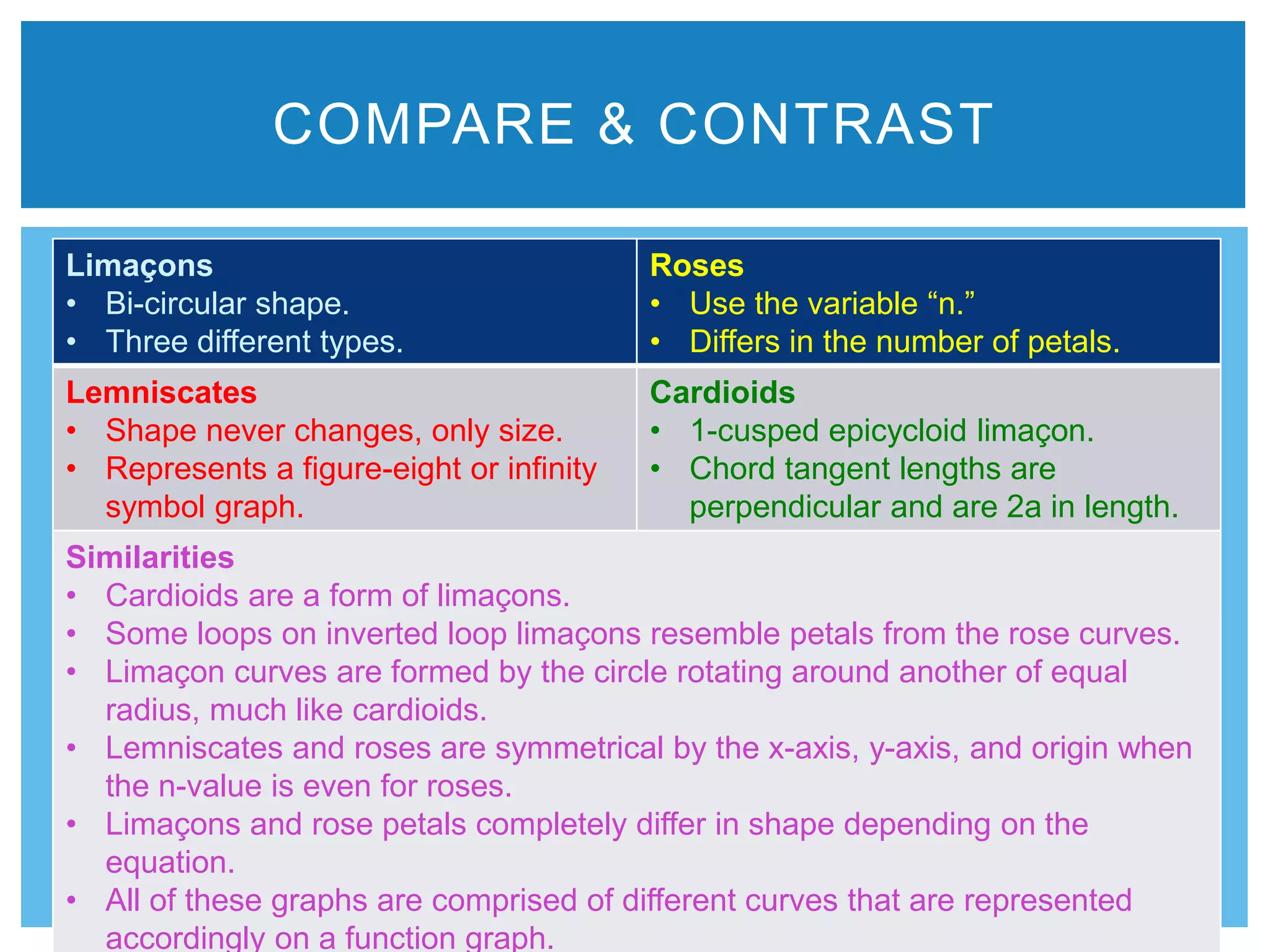
The document describes the learning experience of polar graphs in a precalculus honors class, covering various types such as limaçons, roses, and lemniscates, as well as their mathematical representations and characteristics. It reflects on the difficulty of understanding these graphs and the effectiveness of using TI-Nspire calculators to visualize concepts. The author expressed a desire for supplemental lessons to improve understanding for future calculus students.

1. Nicholas
Portugal
Precalculus
Honors
Period A7
POLAR
GRAPHS

2.  During the last few weeks of pre-calculus, we learned a
variety of different polar graphs through five packet
activities using the TI-Nspire calculators.
 Polar graphs are essentially graphs on a circular coordinate
plane compared to the conventional rectangular planes.
 Polar graphs can be represented using function graphs,
which are comprised of sine waves that follow a distinct
pattern to represent different components of the polar graph.
 While polar graphs can be represented using function
graphs, as they both contain angular measurements, we
also learned how to convert ‘polar coordinates’ (e.g. 5,90º)
to ‘rectangular’ coordinates ([5 x cos 90],[5 x sin 90]  0,5)
using respective sine and cosine formulas to differentiate
between both ‘x’ and ‘y’ on the rectangular coordinate plane.
OVERVIEW

3.  Old French word for
‘snails.’
 Bi-circular shape.
 Three types: Looped,
dimpled, convex.
 r = a ± b (cos θ) or r = a ±
b (sin θ)
 Looped: |a/b| < 1
 Dimpled: 1 < |a/b| < 2
 Convex: |a/b| ≥ 2
 Circular: r = a (cos θ) or r
= a (sin θ)
 Curves are formed as the
circle rotates around
another of equal radius.
LIMAÇONS

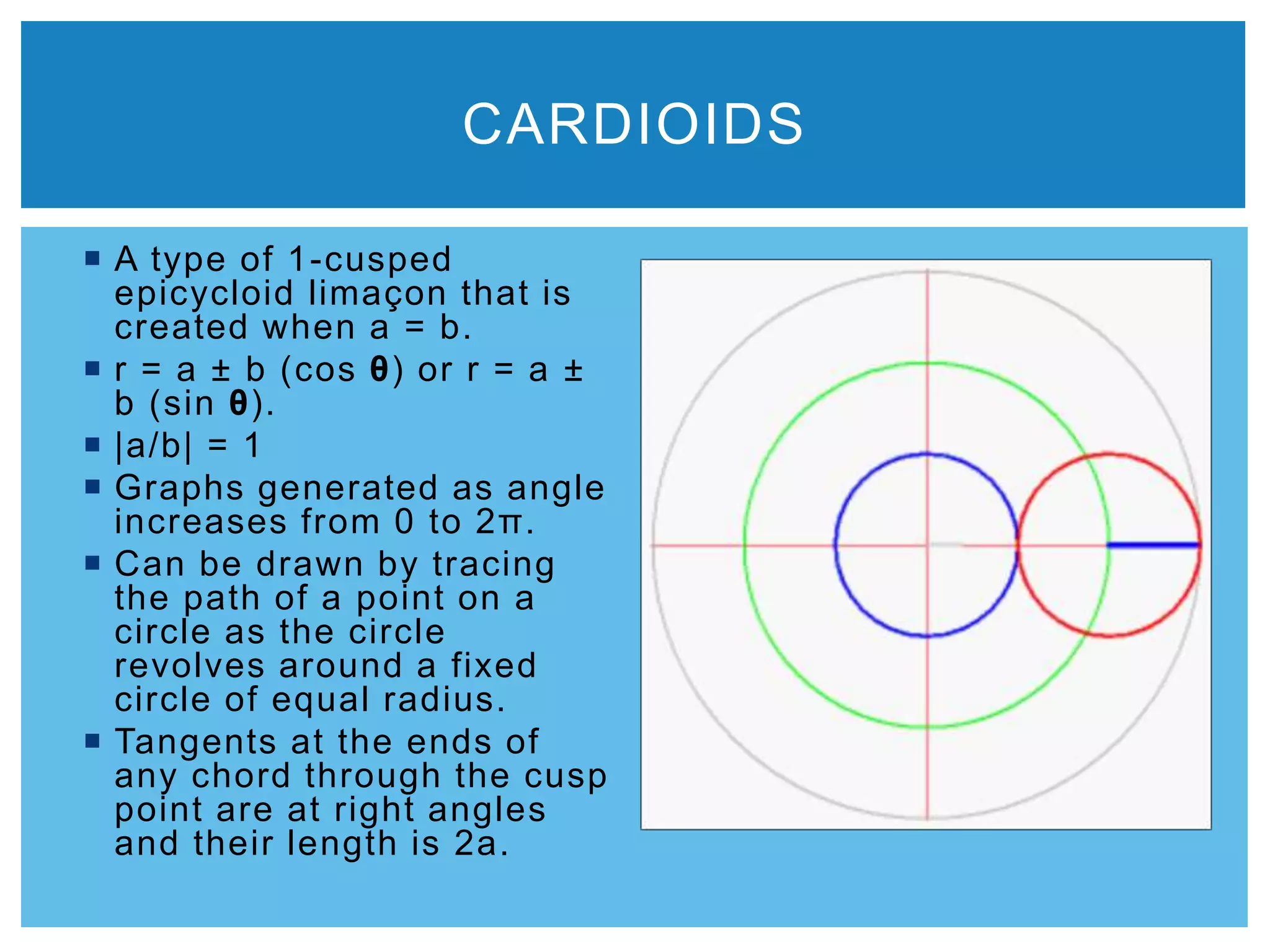
4.  Named for its flowery
petals that extend from the
origin.
 r = a [cos (nθ)] or r = a [sin
(nθ)]
 Odd # of Petals: When n is
odd (n). Curves formed as
it increases from 0 to π.
 Even # of Petals: When n
is even (2n). Curves
formed as it increases from
0 to 2π.
 If n is even, the graph is
symmetric about the x-
axis, y-axis, and the origin.
 Depending on the n value,
the graph will be shaped in
a particular way.
ROSES

5.  Shaped like an infinity
symbol or figure-eight.
 r2 = a2 [cos (2θ)] or r2
= a2 [sin (2θ)].
 r = ±√a2 [cos (2θ)] or r
= ±√a2 [sin (2θ)].
 a ≠ 0
 Graphs are generated
as the angle increases
gradually from 0 to 2π.
 Symmetrical across
the x-axis, y-axis, and
the origin.
LEMNISCATES

6.  A type of 1-cusped
epicycloid limaçon that is
created when a = b.
 r = a ± b (cos θ) or r = a ±
b (sin θ).
 |a/b| = 1
 Graphs generated as angle
increases from 0 to 2π.
 Can be drawn by tracing
the path of a point on a
circle as the circle
revolves around a fixed
circle of equal radius.
 Tangents at the ends of
any chord through the cusp
point are at right angles
and their length is 2a.
CARDIOIDS

7. Limaçons
• Bi-circular shape.
• Three different types.
Roses
• Use the variable “n.”
• Differs in the number of petals.
Lemniscates
• Shape never changes, only size.
• Represents a figure-eight or infinity
symbol graph.
Cardioids
• 1-cusped epicycloid limaçon.
• Chord tangent lengths are
perpendicular and are 2a in length.
Similarities
• Cardioids are a form of limaçons.
• Some loops on inverted loop limaçons resemble petals from the rose curves.
• Limaçon curves are formed by the circle rotating around another of equal
radius, much like cardioids.
• Lemniscates and roses are symmetrical by the x-axis, y-axis, and origin when
the n-value is even for roses.
• Limaçons and rose petals completely differ in shape depending on the
equation.
• All of these graphs are comprised of different curves that are represented
accordingly on a function graph.
COMPARE & CONTRAST

8.  Overall, the polar unit was perhaps one of the most difficult
units this entire year. I learned from the many mistakes I made
along the way while completing the packets, and using the TI-
Nspire calculators helped me to visualize how the graphs were
drawn, and how they compared with function graphs.
 Using both limaçons and roses together was fascinating
because they correlated so well with each other.
 I was able to learn about a new type of graph from this unit, as
I previously only knew how to graph function graphs and
rectangular graphs.
 After each packet I began to grasp polar graphs even better,
though I did not particularly enjoy only learning through the
lessons on the calculators.
 Finally, if there were one thing to change about this unit, I
would have also provided supplemental lessons on the subject
in addition to the packets to ensure greater understanding,
especially for students taking calculus next year.
SUMMARY