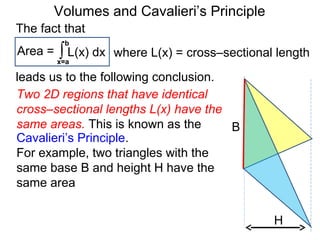
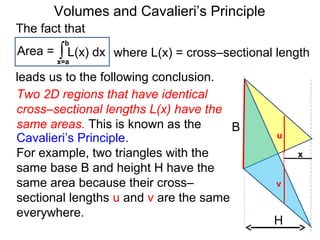
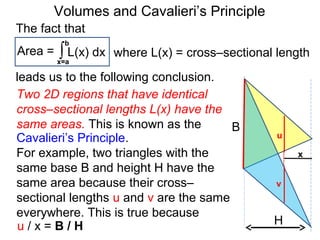
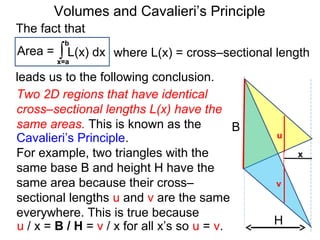
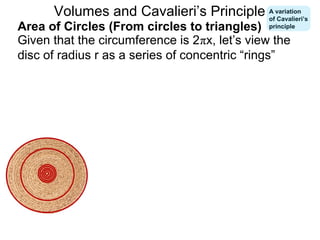
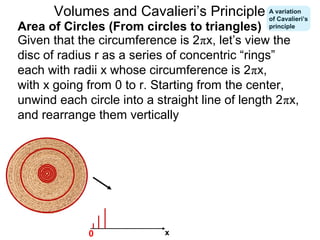
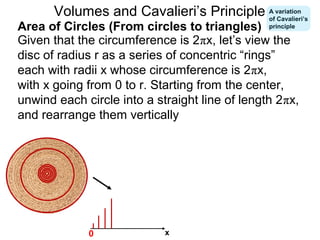
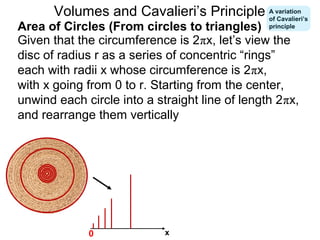
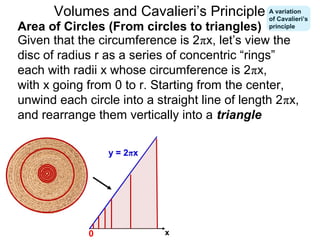
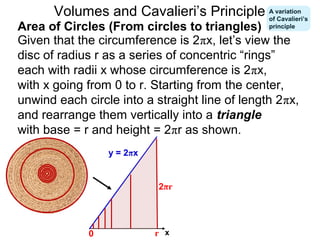
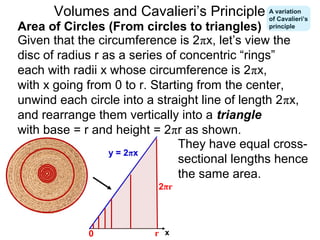
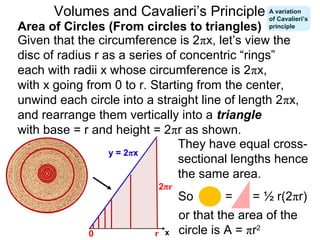
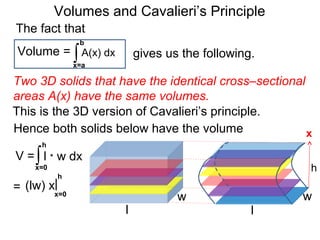
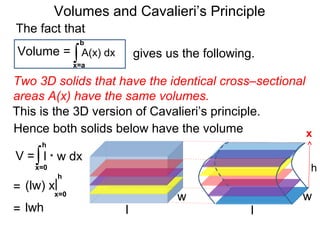
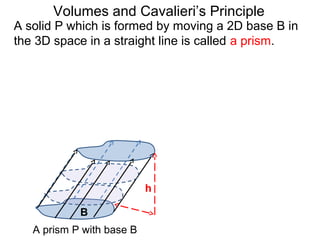
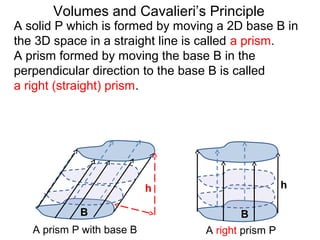
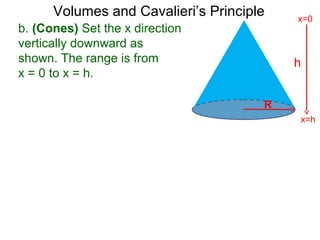
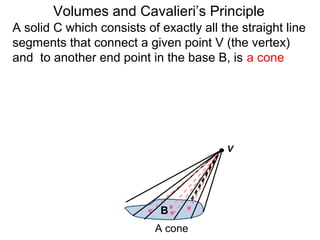
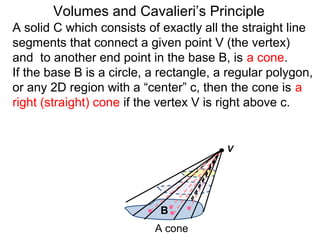
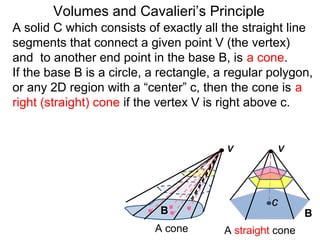
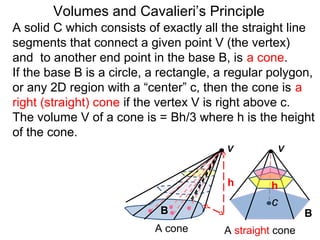
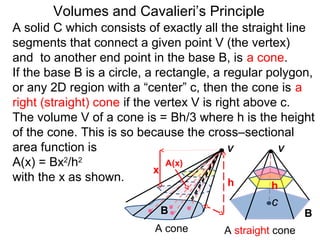
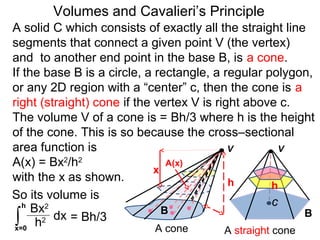
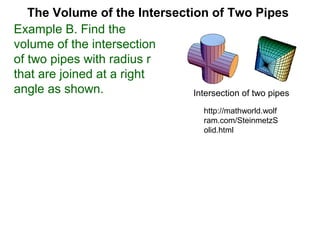
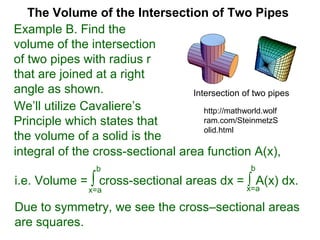
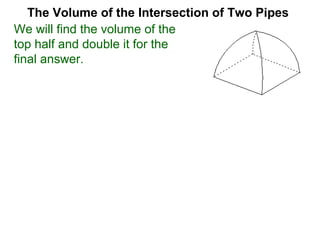
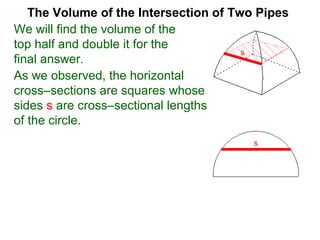
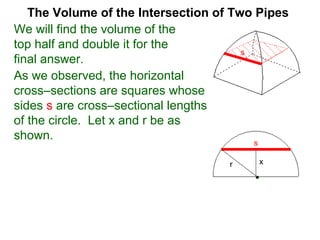
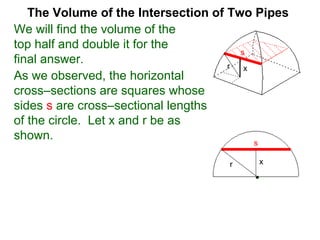
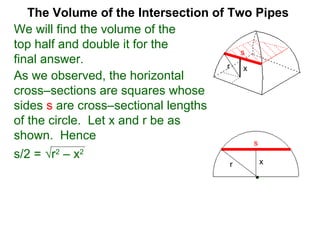
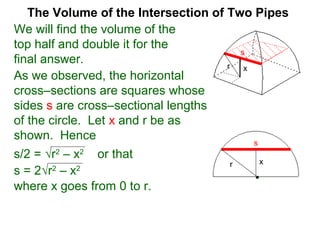
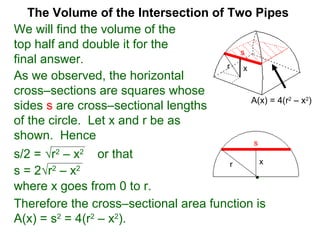
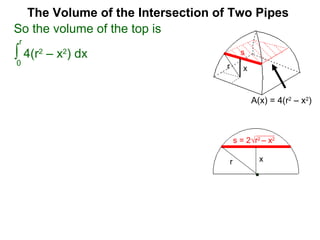
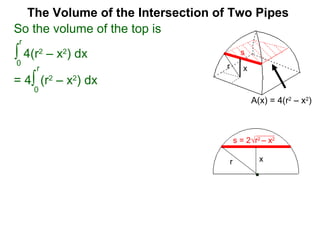
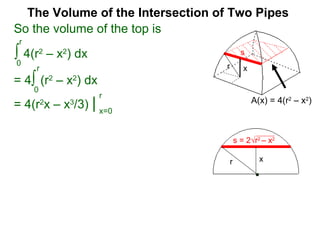
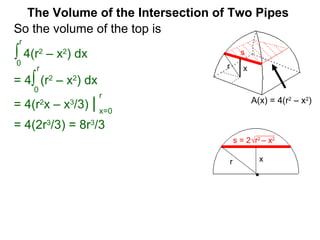
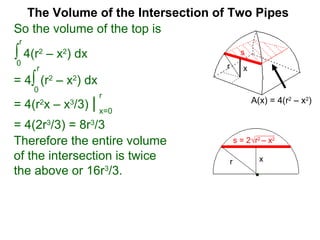
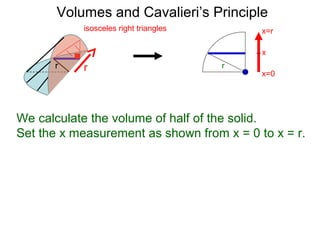
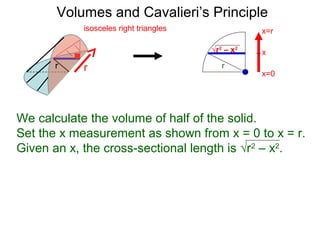
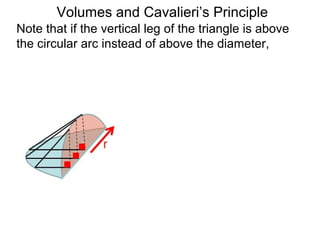
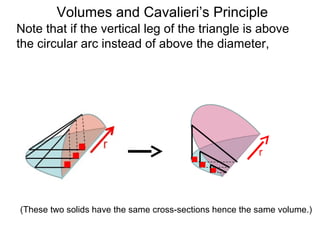
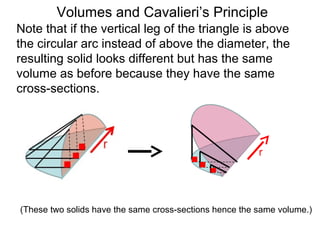
The document discusses Cavalieri's principle, which states that two regions with identical cross-sectional areas have the same volume. It demonstrates this principle by showing how the volume of a circle can be determined by unwinding its concentric rings into a triangle of equal area. The 3D version of the principle is also described, indicating that solids with identical cross-sectional areas have the same volume. Examples of prisms and cones are provided.

1. Volumes and Cavalieri’s Principle
The fact that
Area = ∫x=a
b
L(x) dx
leads us to the following conclusion.
where L(x) = cross–sectional length

2. Volumes and Cavalieri’s Principle
Two 2D regions that have identical
cross–sectional lengths L(x) have the
same areas.
The fact that
Area = ∫x=a
b
L(x) dx
leads us to the following conclusion.
where L(x) = cross–sectional length

3. Volumes and Cavalieri’s Principle
The fact that
Two 2D regions that have identical
cross–sectional lengths L(x) have the
same areas. This is known as the
Area = ∫x=a
b
L(x) dx
leads us to the following conclusion.
Cavalieri’s Principle.
where L(x) = cross–sectional length

4. Volumes and Cavalieri’s Principle
Two 2D regions that have identical
cross–sectional lengths L(x) have the
same areas. This is known as the
Cavalieri’s Principle.
For example, two triangles with the
same base B and height H have the
same area
H
B
The fact that
Area = ∫x=a
b
L(x) dx
leads us to the following conclusion.
where L(x) = cross–sectional length

5. Volumes and Cavalieri’s Principle
Two 2D regions that have identical
cross–sectional lengths L(x) have the
same areas. This is known as the
Cavalieri’s Principle.
For example, two triangles with the
same base B and height H have the
same area because their cross–
sectional lengths u and v are the same
everywhere.
H
B
x
u
v
The fact that
Area = ∫x=a
b
L(x) dx
leads us to the following conclusion.
where L(x) = cross–sectional length

6. Volumes and Cavalieri’s Principle
Two 2D regions that have identical
cross–sectional lengths L(x) have the
same areas. This is known as the
Cavalieri’s Principle.
For example, two triangles with the
same base B and height H have the
same area because their cross–
sectional lengths u and v are the same
everywhere. This is true because
H
B
x
u
v
u / x = B / H
The fact that
Area = ∫x=a
b
L(x) dx
leads us to the following conclusion.
where L(x) = cross–sectional length

7. Volumes and Cavalieri’s Principle
Two 2D regions that have identical
cross–sectional lengths L(x) have the
same areas. This is known as the
Cavalieri’s Principle.
For example, two triangles with the
same base B and height H have the
same area because their cross–
sectional lengths u and v are the same
everywhere. This is true because
H
B
x
u
v
u / x = B / H = v / x for all x’s so u = v.
The fact that
Area = ∫x=a
b
L(x) dx
leads us to the following conclusion.
where L(x) = cross–sectional length

8. Area of Circles (From circles to triangles)
Volumes and Cavalieri’s Principle A variation
of Cavalieri’s
principle

9. Given that the circumference is 2πx, let’s view the
disc of radius r as a series of concentric “rings”
Area of Circles (From circles to triangles)
Volumes and Cavalieri’s Principle A variation
of Cavalieri’s
principle

10. Given that the circumference is 2πx, let’s view the
disc of radius r as a series of concentric “rings”
each with radii x whose circumference is 2πx,
with x going from 0 to r.
Area of Circles (From circles to triangles)
Volumes and Cavalieri’s Principle A variation
of Cavalieri’s
principle

11. Given that the circumference is 2πx, let’s view the
disc of radius r as a series of concentric “rings”
each with radii x whose circumference is 2πx,
with x going from 0 to r. Starting from the center,
unwind each circle into a straight line of length 2πx,
and rearrange them vertically
Area of Circles (From circles to triangles)
Volumes and Cavalieri’s Principle A variation
of Cavalieri’s
principle

12. x0
Given that the circumference is 2πx, let’s view the
disc of radius r as a series of concentric “rings”
each with radii x whose circumference is 2πx,
with x going from 0 to r. Starting from the center,
unwind each circle into a straight line of length 2πx,
and rearrange them vertically
Area of Circles (From circles to triangles)
Volumes and Cavalieri’s Principle A variation
of Cavalieri’s
principle

13. x0
Given that the circumference is 2πx, let’s view the
disc of radius r as a series of concentric “rings”
each with radii x whose circumference is 2πx,
with x going from 0 to r. Starting from the center,
unwind each circle into a straight line of length 2πx,
and rearrange them vertically
Area of Circles (From circles to triangles)
Volumes and Cavalieri’s Principle A variation
of Cavalieri’s
principle

14. x0
Given that the circumference is 2πx, let’s view the
disc of radius r as a series of concentric “rings”
each with radii x whose circumference is 2πx,
with x going from 0 to r. Starting from the center,
unwind each circle into a straight line of length 2πx,
and rearrange them vertically
Area of Circles (From circles to triangles)
Volumes and Cavalieri’s Principle A variation
of Cavalieri’s
principle

15. x0
Given that the circumference is 2πx, let’s view the
disc of radius r as a series of concentric “rings”
each with radii x whose circumference is 2πx,
with x going from 0 to r. Starting from the center,
unwind each circle into a straight line of length 2πx,
and rearrange them vertically
Area of Circles (From circles to triangles)
Volumes and Cavalieri’s Principle A variation
of Cavalieri’s
principle

16. x0
Given that the circumference is 2πx, let’s view the
disc of radius r as a series of concentric “rings”
each with radii x whose circumference is 2πx,
with x going from 0 to r. Starting from the center,
unwind each circle into a straight line of length 2πx,
and rearrange them vertically
Area of Circles (From circles to triangles)
Volumes and Cavalieri’s Principle A variation
of Cavalieri’s
principle

17. x0
y = 2πx
Given that the circumference is 2πx, let’s view the
disc of radius r as a series of concentric “rings”
each with radii x whose circumference is 2πx,
with x going from 0 to r. Starting from the center,
unwind each circle into a straight line of length 2πx,
and rearrange them vertically into a triangle
Area of Circles (From circles to triangles)
Volumes and Cavalieri’s Principle A variation
of Cavalieri’s
principle

18. Given that the circumference is 2πx, let’s view the
disc of radius r as a series of concentric “rings”
each with radii x whose circumference is 2πx,
with x going from 0 to r. Starting from the center,
unwind each circle into a straight line of length 2πx,
and rearrange them vertically into a triangle
with base = r and height = 2πr as shown.
Area of Circles (From circles to triangles)
Volumes and Cavalieri’s Principle
x0
y = 2πx
2πr
r
A variation
of Cavalieri’s
principle

19. Given that the circumference is 2πx, let’s view the
disc of radius r as a series of concentric “rings”
each with radii x whose circumference is 2πx,
with x going from 0 to r. Starting from the center,
unwind each circle into a straight line of length 2πx,
and rearrange them vertically into a triangle
with base = r and height = 2πr as shown.
They have equal cross-
sectional lengths hence
the same area.
Area of Circles (From circles to triangles)
Volumes and Cavalieri’s Principle
x0
y = 2πx
2πr
r
A variation
of Cavalieri’s
principle

20. Given that the circumference is 2πx, let’s view the
disc of radius r as a series of concentric “rings”
each with radii x whose circumference is 2πx,
with x going from 0 to r. Starting from the center,
unwind each circle into a straight line of length 2πx,
and rearrange them vertically into a triangle
with base = r and height = 2πr as shown.
They have equal cross-
sectional lengths hence
the same area.
Area of Circles (From circles to triangles)
= = ½ r(2πr)
or that the area of the
circle is A = πr2
Volumes and Cavalieri’s Principle
x0
y = 2πx
2πr
r
So
A variation
of Cavalieri’s
principle

21. Volumes and Cavalieri’s Principle
∫x=a
b
A(x) dxVolume =
The fact that
gives us the following.

22. Volumes and Cavalieri’s Principle
Two 3D solids that have the identical cross–sectional
areas A(x) have the same volumes.
∫x=a
b
A(x) dxVolume =
The fact that
gives us the following.

23. Volumes and Cavalieri’s Principle
This is the 3D version of Cavalieri’s principle.
Two 3D solids that have the identical cross–sectional
areas A(x) have the same volumes.
∫x=a
b
A(x) dxVolume =
The fact that
gives us the following.

24. Volumes and Cavalieri’s Principle
Two 3D solids that have the identical cross–sectional
areas A(x) have the same volumes.
∫x=a
b
A(x) dxVolume =
The fact that
gives us the following.
Hence both solids below have the volume
l
w
l
w
h
x
This is the 3D version of Cavalieri’s principle.

25. Volumes and Cavalieri’s Principle
Two 3D solids that have the identical cross–sectional
areas A(x) have the same volumes.
∫x=a
b
A(x) dxVolume =
The fact that
gives us the following.
Hence both solids below have the volume
l
w
l
w
h
∫x=0
h
l * w dx
x
V =
This is the 3D version of Cavalieri’s principle.

26. Volumes and Cavalieri’s Principle
Two 3D solids that have the identical cross–sectional
areas A(x) have the same volumes.
∫x=a
b
A(x) dxVolume =
The fact that
gives us the following.
Hence both solids below have the volume
l
w
l
w
h
∫x=0
h
l * w dx
x
= x=0
h
|(lw) x
V =
This is the 3D version of Cavalieri’s principle.

27. Volumes and Cavalieri’s Principle
Two 3D solids that have the identical cross–sectional
areas A(x) have the same volumes.
∫x=a
b
A(x) dxVolume =
The fact that
gives us the following.
Hence both solids below have the volume
l
w
l
w
h
∫x=0
h
l * w dx
x
= x=0
h
|(lw) x
= lwh
V =
This is the 3D version of Cavalieri’s principle.

28. Volumes and Cavalieri’s Principle
Two 3D solids that have the identical cross–sectional
areas A(x) have the same volumes.
∫x=a
b
A(x) dxVolume =
The fact that
Hence both solids below have the volume
l
w
l
w
h
∫x=0
h
l * w dx
x
= x=0
h
|(lw) x
= lwh
V =
Two important solids are the prisms and the cones.
This is the 3D version of Cavalieri’s principle.
gives us the following.

29. A solid P which is formed by moving a 2D base B in
the 3D space in a straight line is called a prism.
Volumes and Cavalieri’s Principle
B
A prism P with base B
h

30. A solid P which is formed by moving a 2D base B in
the 3D space in a straight line is called a prism.
A prism formed by moving the base B in the
perpendicular direction to the base B is called
a right (straight) prism.
Volumes and Cavalieri’s Principle
B B
A prism P with base B A right prism P
h h

31. A solid P which is formed by moving a 2D base B in
the 3D space in a straight line is called a prism.
A prism formed by moving the base B in the
perpendicular direction to the base B is called
a right (straight) prism. Let h be the height of the
prisms as shown, then both prisms have the same
volume V = Bh due to the Cavalieri’s Principle since
they have the same cross-sectional area B.
Volumes and Cavalieri’s Principle
B B
A prism P with base B A right prism P
h h

32. Volumes and Cavalieri’s Principle
In fact, any solid formed by rotating and moving a
base B upward to the height of h, such as the ones
shown here,

33. Volumes and Cavalieri’s Principle
http://www.iroonie.com/modern-modular-indoor-spiral-staircase-designs/modern-woodehttp://www.screen-
dream.de/images/Sharp_
Spiral.jpg
In fact, any solid formed by rotating and moving a
base B upward to the height of h, such as the ones
shown here,

34. Volumes and Cavalieri’s Principle
In fact, any solid formed by rotating and moving a
base B upward to the height of h, such as the ones
shown here, also have volumes V = Bh.
http://www.iroonie.com/modern-modular-
indoor-spiral-staircase-designs/modern-
wooden-spiral-staircase-layouts/
http://www.screen-
dream.de/images/Sharp_
Spiral.jpg

35. Volumes and Cavalieri’s Principle
In fact, any solid formed by rotating and moving a
base B upward to the height of h, such as the ones
shown here, also have volumes V = Bh.
If the staircase here is a continuous ramp, B is the
landing–surface area of the step and h is the height,
then the volume of the ramp would be V = Bh.
http://www.iroonie.com/modern-modular-
indoor-spiral-staircase-designs/modern-
wooden-spiral-staircase-layouts/
http://www.screen-
dream.de/images/Sharp_
Spiral.jpg

36. Volumes and Cavalieri’s Principle
b. (Cones)
h
R

37. Volumes and Cavalieri’s Principle
b. (Cones) Set the x direction
vertically downward as
shown. The range is from
x = 0 to x = h.
h
x=h
x=0
R

38. Volumes and Cavalieri’s Principle
b. (Cones) Set the x direction
vertically downward as
shown. The range is from
x = 0 to x = h.
The cross–sections are
circles of whose radius r
varies according x.
h
x=h
x=0
R
x
r

39. Volumes and Cavalieri’s Principle
b. (Cones) Set the x direction
vertically downward as
shown. The range is from
x = 0 to x = h.
The cross–sections are
circles of whose radius r
varies according x.
r / R = x / h
h
x=h
x=0
R
x
r
By a similar triangles argument we have that

40. Volumes and Cavalieri’s Principle
b. (Cones) Set the x direction
vertically downward as
shown. The range is from
x = 0 to x = h.
The cross–sections are
circles of whose radius r
varies according x.
r / R = x / h or that r = xR
h
By a similar triangles argument we have that
h
x=h
x=0
R
x
r

41. Volumes and Cavalieri’s Principle
b. (Cones) Set the x direction
vertically downward as
shown. The range is from
x = 0 to x = h.
The cross–sections are
circles of whose radius r
varies according x.
r / R = x / h or that r = xR
h
A(x) = π ( 2
therefore
xR
h )
By a similar triangles argument we have that
h
x=h
x=0
R
x
r

42. Volumes and Cavalieri’s Principle
b. (Cones) Set the x direction
vertically downward as
shown. The range is from
x = 0 to x = h.
The cross–sections are
circles of whose radius r
varies according x.
r / R = x / h or that r =
∫x=0
h
dxV =
xR
h
A(x) = π ( 2
therefore
xR
h ) and the volume of the cone is
π ( 2xR
h )
By a similar triangles argument we have that
h
x=h
x=0
R
x
r

43. Volumes and Cavalieri’s Principle
b. (Cones) Set the x direction
vertically downward as
shown. The range is from
x = 0 to x = h.
The cross–sections are
circles of whose radius r
varies according x.
r / R = x / h or that r =
∫x=0
h
dxV =
xR
h
A(x) = π ( 2
therefore
xR
h ) and the volume of the cone is
π ( 2xR
h ) ∫x=0
h
dx=
πR2
h2
By a similar triangles argument we have that
x2
h
x=h
x=0
R
x
r

44. Volumes and Cavalieri’s Principle
b. (Cones) Set the x direction
vertically downward as
shown. The range is from
x = 0 to x = h.
The cross–sections are
circles of whose radius r
varies according x.
r / R = x / h or that r =
∫x=0
h
dxV =
xR
h
A(x) = π ( 2
therefore
xR
h ) and the volume of the cone is
π ( 2xR
h ) ∫x=0
h
dx=
πR2
h2
By a similar triangles argument we have that
x2 |
x=0
h
=
πR2
h2
x3
3
h
x=h
x=0
R
x
r

45. Volumes and Cavalieri’s Principle
b. (Cones) Set the x direction
vertically downward as
shown. The range is from
x = 0 to x = h.
The cross–sections are
circles of whose radius r
varies according x.
r / R = x / h or that r =
h
x=h
x=0
∫x=0
h
dxV =
R
x
r
xR
h
A(x) = π ( 2
therefore
xR
h ) and the volume of the cone is
π ( 2xR
h ) ∫x=0
h
dx=
πR2
h2
By a similar triangles argument we have that
x2 |
x=0
h
==
πR2
h2
x3
3
π R2
h
3

46. A solid C which consists of exactly all the straight line
segments that connect a given point V (the vertex)
and to another end point in the base B, is a cone
Volumes and Cavalieri’s Principle

47. A solid C which consists of exactly all the straight line
segments that connect a given point V (the vertex)
and to another end point in the base B, is a cone
Volumes and Cavalieri’s Principle
B
A cone
V

48. A solid C which consists of exactly all the straight line
segments that connect a given point V (the vertex)
and to another end point in the base B, is a cone.
If the base B is a circle, a rectangle, a regular polygon,
or any 2D region with a “center” c, then the cone is a
right (straight) cone if the vertex V is right above c.
Volumes and Cavalieri’s Principle
B
A cone
V

49. A solid C which consists of exactly all the straight line
segments that connect a given point V (the vertex)
and to another end point in the base B, is a cone.
If the base B is a circle, a rectangle, a regular polygon,
or any 2D region with a “center” c, then the cone is a
right (straight) cone if the vertex V is right above c.
Volumes and Cavalieri’s Principle
B B
A cone A straight cone
V V
c

50. A solid C which consists of exactly all the straight line
segments that connect a given point V (the vertex)
and to another end point in the base B, is a cone.
If the base B is a circle, a rectangle, a regular polygon,
or any 2D region with a “center” c, then the cone is a
right (straight) cone if the vertex V is right above c.
The volume V of a cone is = Bh/3 where h is the height
of the cone.
Volumes and Cavalieri’s Principle
B B
A cone A straight cone
h
V V
c
h

51. Volumes and Cavalieri’s Principle
B B
A cone A straight cone
h
V V
c
h
x
A(x)
A solid C which consists of exactly all the straight line
segments that connect a given point V (the vertex)
and to another end point in the base B, is a cone.
If the base B is a circle, a rectangle, a regular polygon,
or any 2D region with a “center” c, then the cone is a
right (straight) cone if the vertex V is right above c.
The volume V of a cone is = Bh/3 where h is the height
of the cone. This is so because the cross–sectional
area function is
A(x) = Bx2
/h2
with the x as shown.

52. Volumes and Cavalieri’s Principle
B B
A cone A straight cone
h
V V
c
h
x
A(x)
∫x=0
h
dx
Bx2
h2 = Bh/3
A solid C which consists of exactly all the straight line
segments that connect a given point V (the vertex)
and to another end point in the base B, is a cone.
If the base B is a circle, a rectangle, a regular polygon,
or any 2D region with a “center” c, then the cone is a
right (straight) cone if the vertex V is right above c.
The volume V of a cone is = Bh/3 where h is the height
of the cone. This is so because the cross–sectional
area function is
A(x) = Bx2
/h2
with the x as shown.
So its volume is

53. Volume of Spheres (From discs to rings)
Volumes and Cavalieri’s Principle

54. Volume of Spheres (From discs to rings)
Volumes and Cavalieri’s Principle
Given the volume of a cone, we may obtain the volume
of the sphere that V = 4πr3
/3 using the Cavalieri’s
principle.

55. Volume of Spheres (From discs to rings)
Volumes and Cavalieri’s Principle
Given the volume of a cone, we may obtain the volume
of the sphere that V = 4πr3
/3 using the Cavalieri’s
principle. Let’s compare a hemisphere of radius r with
a cylinder of height r and radius r with the cone
removed from its interior.
r
0
r r
r

56. Volume of Spheres (From discs to rings)
Volumes and Cavalieri’s Principle
Given the volume of a cone, we may obtain the volume
of the sphere that V = 4πr3
/3 using the Cavalieri’s
principle. Let’s compare a hemisphere of radius r with
a cylinder of height r and radius r with the cone
removed from its interior.
Selecting x in the direction as shown and let A(x)
r
0
A(x)
r r
r
x

57. Volume of Spheres (From discs to rings)
Volumes and Cavalieri’s Principle
Given the volume of a cone, we may obtain the volume
of the sphere that V = 4πr3
/3 using the Cavalieri’s
principle. Let’s compare a hemisphere of radius r with
a cylinder of height r and radius r with the cone
removed from its interior.
Selecting x in the direction as shown and let A(x)
and B(x) be cross-sectional area functions
respectively.
r
0
A(x) B(x)
r r
r
x

58. Volume of Spheres (From discs to rings)
Volumes and Cavalieri’s Principle
Given the volume of a cone, we may obtain the volume
of the sphere that V = 4πr3
/3 using the Cavalieri’s
principle. Let’s compare a hemisphere of radius r with
a cylinder of height r and radius r with the cone
removed from its interior.
Selecting x in the direction as shown and let A(x)
and B(x) be cross-sectional area functions
respectively.
r
0
A(x) B(x)
We claim that A(x) = B(x), hence by the Cavaliers’s
principle that they have the same volume.
r r
r
x

59. Volume of Spheres (From discs to rings)
Volumes and Cavalieri’s Principle
r
0
x r
At height x, the cross-sectional
area of the hemisphere is a
circle of radius √r2
– x2
,
so A(x) = π(r2
– x2
).
At height x, the cross-sectional
area of cylinder-minus-the-cone
is a ring. The outer radius of the
ring is r, its inner radius is x,
hence B(x) = πr2
– πx2
= A(x). r
x
So the two solids have the same
volume and that the volume of
the hemisphere is the volume of
the cylinder-minus-the-cone or πr3
– 1/3 πr3
= 2/3
B(x)
√r2
– x2

60. Volume of Spheres (From discs to rings)
Volumes and Cavalieri’s Principle
r
0
x r
At height x, the cross-sectional
area of the hemisphere is a
circle of radius √r2
– x2
,
√r2
– x2
A(x)

61. Volume of Spheres (From discs to rings)
Volumes and Cavalieri’s Principle
r
0
x r
At height x, the cross-sectional
area of the hemisphere is a
circle of radius √r2
– x2
,
so A(x) = π(r2
– x2
).
√r2
– x2
A(x)

62. Volume of Spheres (From discs to rings)
Volumes and Cavalieri’s Principle
r
0
x r
At height x, the cross-sectional
area of the hemisphere is a
circle of radius √r2
– x2
,
so A(x) = π(r2
– x2
).
At height x, the cross-sectional
area of cylinder-minus-the-cone
is a ring.
r
x
B(x)
√r2
– x2
A(x)

63. Volume of Spheres (From discs to rings)
Volumes and Cavalieri’s Principle
r
0
x r
At height x, the cross-sectional
area of the hemisphere is a
circle of radius √r2
– x2
,
so A(x) = π(r2
– x2
).
At height x, the cross-sectional
area of cylinder-minus-the-cone
is a ring. The outer radius of the
ring is r, its inner radius is x,
hence B(x) = πr2
– πx2
= A(x). r
x
B(x)
√r2
– x2
A(x)

64. Volume of Spheres (From discs to rings)
Volumes and Cavalieri’s Principle
r
0
x r
At height x, the cross-sectional
area of the hemisphere is a
circle of radius √r2
– x2
,
so A(x) = π(r2
– x2
).
At height x, the cross-sectional
area of cylinder-minus-the-cone
is a ring. The outer radius of the
ring is r, its inner radius is x,
hence B(x) = πr2
– πx2
= A(x). r
x
So the two solids have the same
volume and that the volume of
the hemisphere is the volume of
the cylinder-minus-the-cone or πr3
– 1/3 πr3
= 2/3 πr3
.
B(x)
√r2
– x2
A(x)

65. The Volume of the Intersection of Two Pipes
Example B. Find the
volume of the intersection
of two pipes with radius r
that are joined at a right
angle as shown. Intersection of two pipes
http://mathworld.wolf
ram.com/SteinmetzS
olid.html

66. The Volume of the Intersection of Two Pipes
integral of the cross-sectional area function A(x)
We’ll utilize Cavaliere’s
Principle which states that
the volume of a solid is the
Example B. Find the
volume of the intersection
of two pipes with radius r
that are joined at a right
angle as shown. Intersection of two pipes
http://mathworld.wolf
ram.com/SteinmetzS
olid.html

67. The Volume of the Intersection of Two Pipes
integral of the cross-sectional area function A(x),
We’ll utilize Cavaliere’s
Principle which states that
the volume of a solid is the
Due to symmetry, we see the cross–sectional areas
are squares.
i.e. Volume = ∫ cross-sectional areas dx = ∫ A(x) dx.
x=a x=a
bb
Example B. Find the
volume of the intersection
of two pipes with radius r
that are joined at a right
angle as shown. Intersection of two pipes
http://mathworld.wolf
ram.com/SteinmetzS
olid.html

68. The Volume of the Intersection of Two Pipes
We will find the volume of the
top half and double it for the
final answer.

69. The Volume of the Intersection of Two Pipes
We will find the volume of the
top half and double it for the
final answer.
As we observed, the horizontal
cross–sections are squares

70. The Volume of the Intersection of Two Pipes
We will find the volume of the
top half and double it for the
final answer.
s
As we observed, the horizontal
cross–sections are squares whose
sides s are cross–sectional lengths
of the circle.
s

71. The Volume of the Intersection of Two Pipes
We will find the volume of the
top half and double it for the
final answer.
As we observed, the horizontal
cross–sections are squares whose
sides s are cross–sectional lengths
of the circle. Let x and r be as
shown.
s
xr
s

72. The Volume of the Intersection of Two Pipes
We will find the volume of the
top half and double it for the
final answer.
As we observed, the horizontal
cross–sections are squares whose
sides s are cross–sectional lengths
of the circle. Let x and r be as
shown.
s
xr
xr
s

73. The Volume of the Intersection of Two Pipes
We will find the volume of the
top half and double it for the
final answer.
As we observed, the horizontal
cross–sections are squares whose
sides s are cross–sectional lengths
of the circle. Let x and r be as
shown. Hence
s/2 = √r2
– x2
s
xr
xr
s

74. The Volume of the Intersection of Two Pipes
We will find the volume of the
top half and double it for the
final answer.
As we observed, the horizontal
cross–sections are squares whose
sides s are cross–sectional lengths
of the circle. Let x and r be as
shown. Hence
s/2 = √r2
– x2
or that
s
xr
s = 2√r2
– x2
where x goes from 0 to r.
xr
s

75. The Volume of the Intersection of Two Pipes
We will find the volume of the
top half and double it for the
final answer.
As we observed, the horizontal
cross–sections are squares whose
sides s are cross–sectional lengths
of the circle. Let x and r be as
shown. Hence
s/2 = √r2
– x2
or that
s
xr
s = 2√r2
– x2
where x goes from 0 to r.
Therefore the cross–sectional area function is
A(x) = s2
= 4(r2
– x2
).
A(x) = 4(r2
– x2
)
xr
s

76. The Volume of the Intersection of Two Pipes
So the volume of the top is
∫ 4(r2
– x2
) dx
0
r
x=a
b
s = 2√r2
– x2
s
xr
A(x) = 4(r2
– x2
)
xr
s

77. The Volume of the Intersection of Two Pipes
So the volume of the top is
∫ 4(r2
– x2
) dx
0
r
x=a
b
s = 2√r2
– x2
s
xr
= 4∫ (r2
– x2
) dx
0
r
A(x) = 4(r2
– x2
)
xr
s

78. The Volume of the Intersection of Two Pipes
So the volume of the top is
∫ 4(r2
– x2
) dx
0
r
x=a
b
s = 2√r2
– x2
s
xr
= 4∫ (r2
– x2
) dx
0
r
= 4(r2
x – x3
/3) | x=0
r
A(x) = 4(r2
– x2
)
xr
s

79. The Volume of the Intersection of Two Pipes
So the volume of the top is
∫ 4(r2
– x2
) dx
0
r
x=a
b
s = 2√r2
– x2
s
xr
= 4∫ (r2
– x2
) dx
0
r
= 4(r2
x – x3
/3) | x=0
r
= 4(2r3
/3) = 8r3
/3
A(x) = 4(r2
– x2
)
xr
s

80. The Volume of the Intersection of Two Pipes
So the volume of the top is
∫ 4(r2
– x2
) dx
0
r
x=a
b
s = 2√r2
– x2
s
xr
Therefore the entire volume
of the intersection is twice
the above or 16r3
/3.
= 4∫ (r2
– x2
) dx
0
r
= 4(r2
x – x3
/3) | x=0
r
= 4(2r3
/3) = 8r3
/3
A(x) = 4(r2
– x2
)
xr
s

81. Volumes and Cavalieri’s Principle
Following are more examples of solids whose
cross–sectional areas are tractable so that we may
use the Cavalieri’s principle to find their volumes.
One group of such solids has cross–sectional areas
that are formed from the linear cross–sections of the
base regions of the solids.

82. Volumes and Cavalieri’s Principle
Following are more examples of solids whose
cross–sectional areas are tractable so that we may
use the Cavalieri’s principle to find their volumes.
One group of such solids has cross–sectional areas
that are formed from the linear cross–sections of the
base regions of the solids.
A solid has a semi–circular
disc of radius r as base.
Its cross-sections,
perpendicular to the
diameter of the base, are
isosceles right triangles as
shown. Find its volume.
Example A.

83. Volumes and Cavalieri’s Principle
Following are more examples of solids whose
cross–sectional areas are tractable so that we may
use the Cavalieri’s principle to find their volumes.
One group of such solids has cross–sectional areas
that are formed from the linear cross–sections of the
base regions of the solids.
Example A.
A solid has a semi–circular
disc of radius r as base.
Its cross-sections,
perpendicular to the
diameter of the base, are
isosceles right triangles as
shown. Find its volume.
r

84. Volumes and Cavalieri’s Principle
Following are more examples of solids whose
cross–sectional areas are tractable so that we may
use the Cavalieri’s principle to find their volumes.
One group of such solids has cross–sectional areas
that are formed from the linear cross–sections of the
base regions of the solids.
Example A.
A solid has a semi–circular
disc of radius r as base.
Its cross-sections,
perpendicular to the
diameter of the base, are
isosceles right triangles as
shown. Find its volume.
r

85. Volumes and Cavalieri’s Principle
We calculate the volume of half of the solid.
r

86. Volumes and Cavalieri’s Principle
r
isosceles right triangles
We calculate the volume of half of the solid.

87. Volumes and Cavalieri’s Principle
rr
isosceles right triangles
We calculate the volume of half of the solid.

88. Volumes and Cavalieri’s Principle
r
We calculate the volume of half of the solid.
Set the x measurement as shown from x = 0 to x = r.
rr
isosceles right triangles
x=0
x=r
x

89. Volumes and Cavalieri’s Principle
√r2
– x2
r
We calculate the volume of half of the solid.
Set the x measurement as shown from x = 0 to x = r.
Given an x, the cross-sectional length is √r2
– x2
.
rr
isosceles right triangles
x=0
x=r
x

90. Volumes and Cavalieri’s Principle
So the cross-section of the solid is a right isosceles
triangle with area ½ (√r2
– x2
)2
= ½ (r2
– x2
).
√r2
– x2
r
We calculate the volume of half of the solid.
Set the x measurement as shown from x = 0 to x = r.
Given an x, the cross-sectional length is √r2
– x2
.
rr
isosceles right triangles
x=0
x=r
x

91. Volumes and Cavalieri’s Principle
So the cross-section of the solid is a right isosceles
triangle with area ½ (√r2
– x2
)2
= ½ (r2
– x2
).
So the volume of the entire solid (two halves) is
∫x=0
r
dxr2
– x2
√r2
– x2
r
We calculate the volume of half of the solid.
Set the x measurement as shown from x = 0 to x = r.
Given an x, the cross-sectional length is √r2
– x2
.
rr
isosceles right triangles
x=0
x=r
x

92. Volumes and Cavalieri’s Principle
So the cross-section of the solid is a right isosceles
triangle with area ½ (√r2
– x2
)2
= ½ (r2
– x2
).
So the volume of the entire solid (two halves) is
∫x=0
r
dxr2
– x2
= r2
x – x3
3 x=0
r
√r2
– x2
r
We calculate the volume of half of the solid.
Set the x measurement as shown from x = 0 to x = r.
Given an x, the cross-sectional length is √r2
– x2
.
rr
isosceles right triangles
x=0
x=r
x

93. Volumes and Cavalieri’s Principle
So the cross-section of the solid is a right isosceles
triangle with area ½ (√r2
– x2
)2
= ½ (r2
– x2
).
So the volume of the entire solid (two halves) is
∫x=0
r
dxr2
– x2
= r2
x – x3
3 x=0
r
= 2r3
3
x=0
x=r
x√r2
– x2
r
We calculate the volume of half of the solid.
Set the x measurement as shown from x = 0 to x = r.
Given an x, the cross-sectional length is √r2
– x2
.
rr
isosceles right triangles

94. Volumes and Cavalieri’s Principle
Note that if the vertical leg of the triangle is above
the circular arc instead of above the diameter,

95. Volumes and Cavalieri’s Principle
Note that if the vertical leg of the triangle is above
the circular arc instead of above the diameter,
(These two solids have the same cross-sections hence the same volume.)
r

96. Volumes and Cavalieri’s Principle
Note that if the vertical leg of the triangle is above
the circular arc instead of above the diameter, the
resulting solid looks different but has the same
volume as before because they have the same
cross-sections.
(These two solids have the same cross-sections hence the same volume.)
r
‘

97. The Volume of the Intersection of Two Pipes
Cavalieri’s Principle gives the mathematical meaning
of “volumes”. Starting with 1D objects – line segments,
we define their “volumes” to be the lengths of the
segments. The “volumes” of 2D regions, i.e. areas,
are the integrals of the cross–sectional–length
functions L(x) which are “volumes of 1D line”
segments. Similarly, the volumes of 3D solids are the
integrals of the cross–sectional–area functions A(x)
which are “volumes” of 2D regions. Continuing in this
manner, we define algebraically the term “volume”
in the “higher dimensional spaces” : volumes of an
object is the integral of the “cross-sectional functions
In one less dimensional space so objects with the
same cross-sectional function have the same volume.