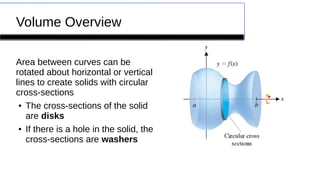
This document provides an overview of calculating volumes of solids using the disk and washer methods. It defines key concepts like using the disk method when the cross-sections are disks and the washer method when there is a hole. Examples are given of how to present these methods using a cucumber and cantaloupe. Remediation resources like videos are suggested to help with common issues like determining radii and limits of integration. Finally, several past AP exam questions involving volumes of revolution are referenced.

1. AP Calculus AB
Volume: Using Disks
and Washers
Jeff Blake
Matt Braddock
Elisabeth Mueller

2. Volume Overview
Area between curves can be
rotated about horizontal or vertical
lines to create solids with circular
cross-sections
● The cross-sections of the solid
are disks
● If there is a hole in the solid, the
cross-sections are washers

3. Volume Overview
Approximates the volume of a
solid by summing the
volumes of the cross-sections
with width Δx, then uses the
limit to shrink the widths to
zero.
Equations
● Disk Method:
R(x) is the radius of the disk
● Washer Method:
R(x) is the outside radius of the
washer, and r(x) is the inside radius
of the washer.

4. Essential Understanding
● Find the intersection(s) of
the graphs and use them
as limits of integration
● Find the area of the
region between the graph
and the axis, or between
two graphs
● Determine when to use the
disk method and when to use
the washer method
● Determine the outside and
inside radii of a washer
● Determine when to integrate
with respect to x and when to
integrate with respect to y

5. Issues with Content
● Determining which variable to
integrate with respect to
● Determining the radius/radii of the
cross-section (especially when
the axis of revolution is not the x-
or y-axis)
● Determining limits of integration
when functions intersect

6. Presenting Volume
● A cucumber is
approximately a cylinder
(removing the ends makes
this more apparent)
● Throughout the cucumber,
the radius is inconsistent, so
the volume formula does not
apply
● Can cut the cucumber into
disks with a consistent
radius, determine the volume
of each disk, then sum the
volumes

7. Presenting Volume
Similarly, you can cut a
cantaloupe in half and
remove the pulp, then you
can identify cross-sections
that are washers.

8. Remediation
Remediation Videos
● Finding zeros and intersects
with the TI-84 (video)
● Finding area underneath a
curve (video)
● Evaluating integrals
analytically (video)
Video Lessons for Volume
● Educreations
– Introduction (video)
– Additional problems (video)
● Khan Academy
– Set of lessons (video)

9. AP Free Response Questions
1998 AB1 2006 AB1
1999 AB2 2006B AB1
2000 AB1 2007 AB1
2001 AB1 2007B AB1
2002 AB1 2008B AB1
2002B AB1 2009 AB4*
2003 AB1 2009B AB4*
2003B AB1 2010 AB4*
2004 AB2 2010B AB1
2004B AB1 2011 AB3*
2005 AB1 2013 AB5*
2005B AB1 2014 AB2
Volume of a solid of revolution
● Appears on nearly every
AP Calculus AB exam
● Until recently, always
calculator active
● 24 free response questions
available on AP Central
*Graphing Calculator Non-Active

10. 2010 Exam Form B #1
Find the volume of
the solid generated
when R is revolved
about the horizontal
line y = 6.

11. 2014 Exam #2
Find the volume of
the solid generated
when R is rotated
about the horizontal
line y = -2.

12. 2008 Exam Form B #1
Find the volume of
the solid generated
when R is rotated
about the vertical line
x = -1.

13. 2008 Exam Form B #1
Find the volume of
the solid generated
when R is rotated
about the vertical line
x = -1.

14. Opportunities for Technology
● Calculators are used to
find intersections of graphs
and compute volume
integrals
● Visual representations of
creating solids available
online (disk method;
washer method)
● Calculus in Motion for
Geometer's Sketchpad