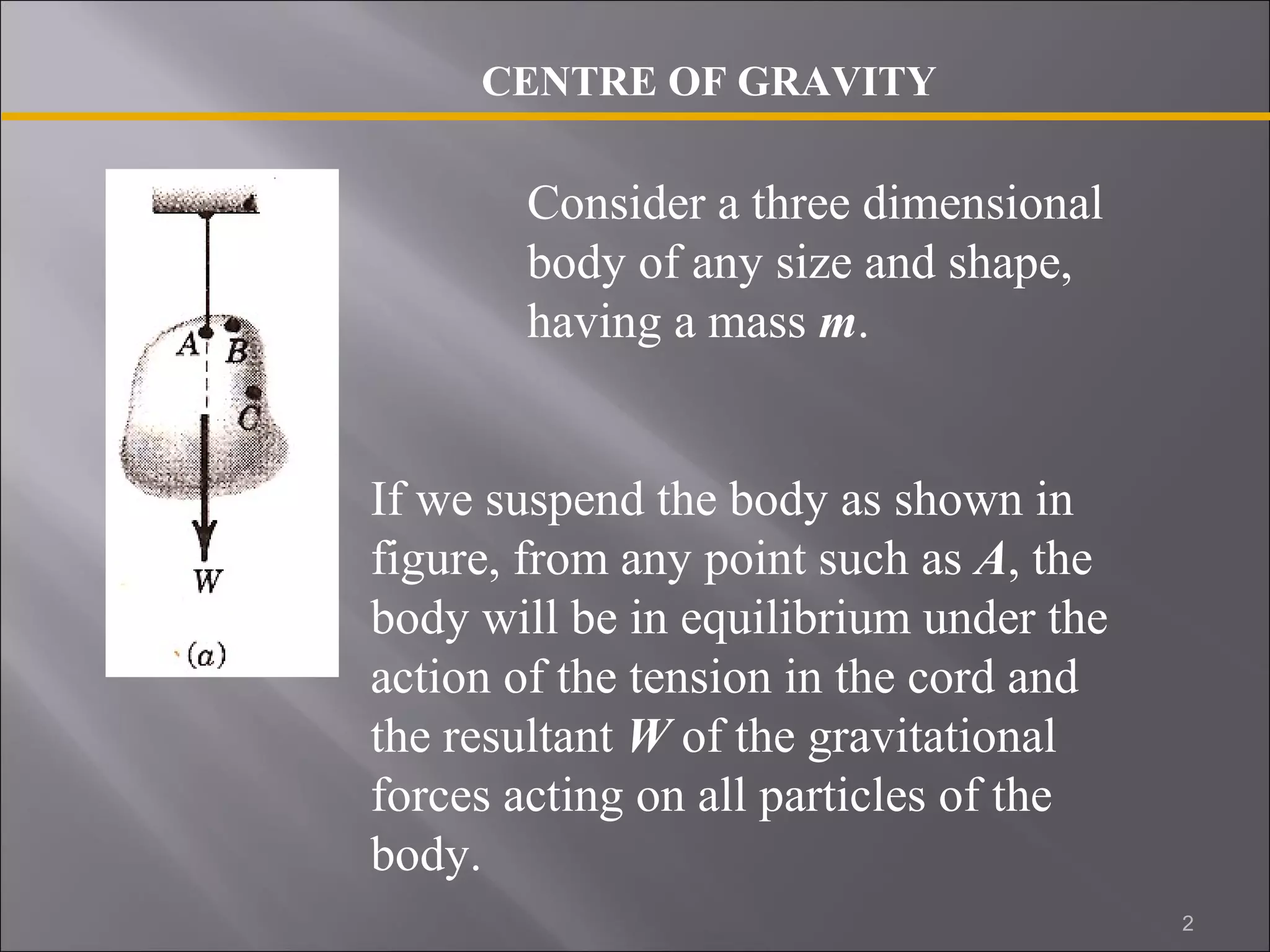
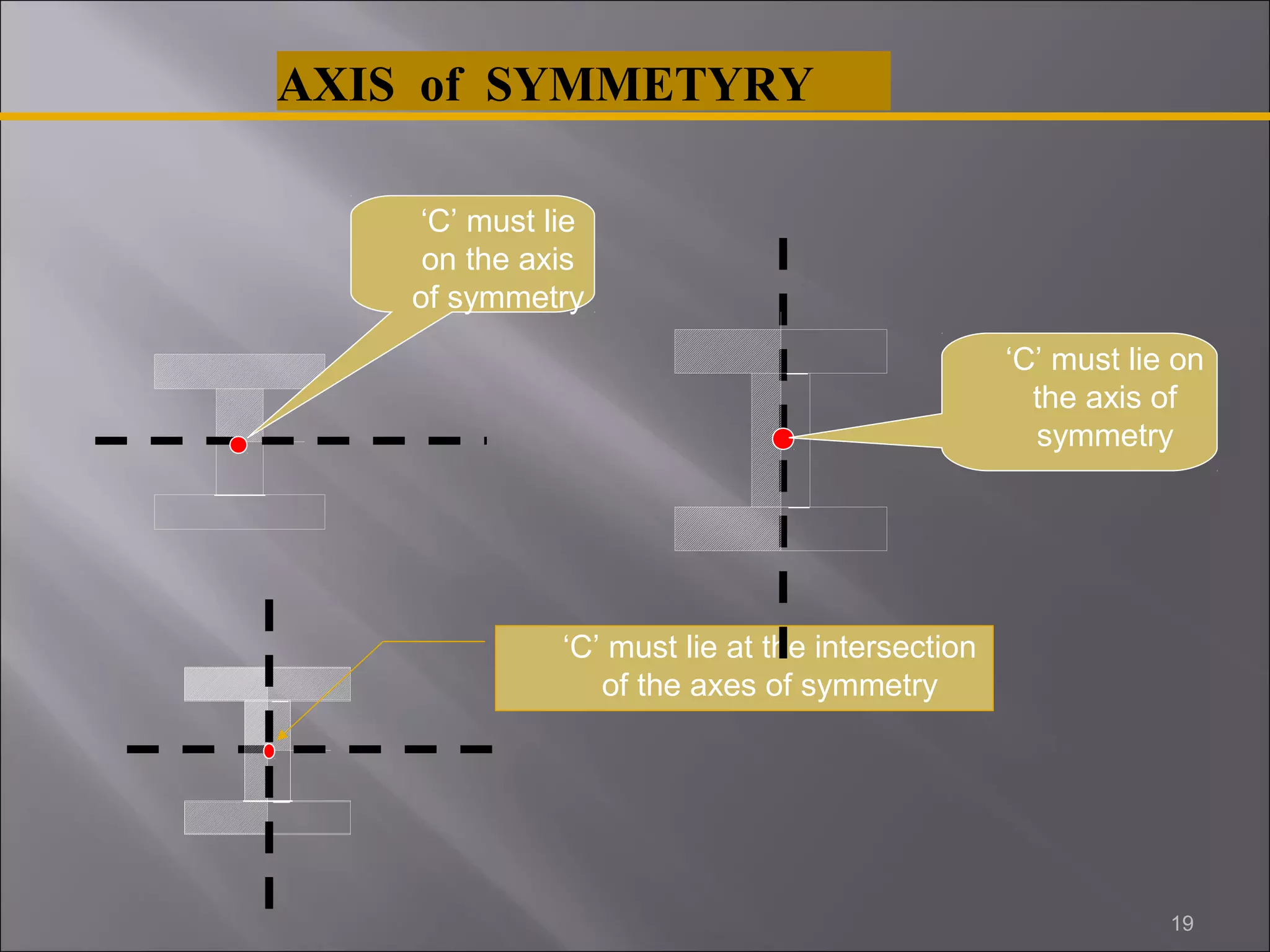
The document discusses the concept of the center of gravity or centroid of a body. It defines the center of gravity as the point where the entire weight of a body can be considered to be concentrated. The center of gravity is determined by the distribution of mass in the body. The document outlines different methods for calculating the centroid based on whether the body can be modeled as a line, area, or volume. It also notes that if a body has an axis of symmetry, its centroid must lie along that axis, or at the intersection of axes if it has multiple symmetries.

1. CENTROID
CENTRE OF GRAVITY
Centre of gravity : It of a body is the point at
which the whole weight of the body may be
assumed to be concentrated.
A body is having only one center of gravity for
all positions of the body.
It is represented by CG. or simply G or C.
1

2. CENTRE OF GRAVITY
Consider a three dimensional
body of any size and shape,
having a mass m.
If we suspend the body as shown in
figure, from any point such as A, the
body will be in equilibrium under the
action of the tension in the cord and
the resultant W of the gravitational
forces acting on all particles of the
body.
2

3. CENTRE OF GRAVITY
Resultant W is collinear with
the Cord
Assume that we mark its
position by drilling a
hypothetical hole of negligible
size along its line of action
3

4. CENTRE OF GRAVITY
To determine mathematically the location of the
centre of gravity of any body,
we apply the principle of moments to the parallel
system of gravitational forces.
Centre of gravity is that point about which the
summation of the first moments of the weights of
the elements of the body is zero.
4

5. CENTRE OF GRAVITY
We repeat the experiment by
suspending the body from other
points such as B and C, and in
each instant we mark the line of
action of the resultant force.
For all practical purposes these lines of action will be
concurrent at a single point G, which is called the
centre of gravity of the body.
5

6. A
A
w
B
w
A
G
B
A
w
A
B
C
B G
A
C
C
B
Example:
CENTRE OF GRAVITY
6

7. CENTRE OF GRAVITY
The moment of the
resultant gravitational
force W, about any
axis
=
the algebraic sum of the
moments about the same
axis of the gravitational
forces dW acting on all
infinitesimal elements of
the body.
if, we apply principle of moments, (Varignon’s Theorem)
about y-axis, for example,
ò x´ dW
7
The moment of the
resultant about y-axis =
The sum of moments of its
components about y-axis

8. CENTRE OF GRAVITY
where = x- x coordinate of centre of gravity
x ò ×
x dW
W
=
Similarly, y and z coordinates of the centre of gravity are
y ò ×
y dW
W
=
z ò ×
z dW
W
=
8
and ----(1)

9. x ò ×
CENTRE OF MASS
x dW
W
=
y ò ×
y dW
, =
,
W
z ò ×
z dW
W
=
With the substitution of W= m g and dW = g dm
(if ‘g’ is assumed constant for all particles, then )
the expression for the coordinates of centre of gravity become
x ò ×
x dm
m
=
y ò ×
y dm
m
=
z ò ×
z dm
m
=
----(1)
, , ----(2)
9

10. CENTRE OF MASS
The density ρ of a body is mass per unit volume. Thus,
the mass of a differential element of volume dV
becomes dm = ρ dV .
If ρ is not constant throughout the body, then we may
write the expression as
x dV
ò
ò
× r
×
×
=
dV
x
r
y dV
ò
ò
× r
×
×
=
dV
y
r
z dV
and ----(3)
ò
ò
× r
×
×
=
dV
z
r
,
10

11. x ò ×
x dm
m
=
CENTRE OF MASS
y ò ×
y dm
, , = ----(2)
m
=
z ò ×
z dm
m
Equation 2 is independent of g and therefore define a
unique point in the body which is a function solely of the
distribution of mass.
This point is called the centre of mass and clearly
coincides with the centre of gravity as long as the gravity
field is treated as uniform and parallel.
11

12. x dV
ò
× r
×
y × r
×
dV
z × r
×
dV
, and ----(3)
When the density ρ of a body is uniform throughout,
it will be a constant factor in both the numerators and
denominators of equation (3) and will therefore
cancel.
The remaining expression defines a purely
geometrical property of the body.
ò
×
=
dV
x
r
ò
ò
×
=
dV
y
r
ò
ò
×
=
dV
z
r
CENTROID
12

13. When speaking of an actual physical body, we use the
term “centre of mass”.
The term centroid is used when the calculation concerns
a geometrical shape only.
Calculation of centroid falls within three distinct
categories, depending on whether we can model the
shape of the body involved as a line, an area or a
volume.
13

14. The centroid “C” of the line segment,
LINES: for a slender rod or a wire of length L, cross-sectional
area A, and density ρ, the body approximates a
line segment, and dm = ρA dL. If ρ and A are constant over
the length of the rod, the coordinates of the centre of mass
also becomes the coordinates of the centroid, C of the line
segment, which may be written as
x ò ×
x dL
L
=
y ò ×
y dL
L
=
z ò ×
z dL
L
=
, ,
14

15. The centroid “C” of the Area segment,
AREAS: when the density ρ, is constant and the
body has a small constant thickness t, the body can be
modeled as a surface area.
The mass of an element becomes dm = ρ t dA.
If ρ and t are constant over entire area, the
coordinates of the ‘centre of mass’ also becomes
the coordinates of the centroid, C of the surface
area and which may be written as
x ò ×
x dA
A
=
y ò ×
y dA
A
=
z ò ×
z dA
A
=
, ,
15

16. VOLUMES: for a general body of volume V and density ρ,
the element has a mass dm = ρ dV .
If the density is constant the coordinates of the centre of
mass also becomes the coordinates of the centroid, C of the
volume and which may be written as
x ò ×
x dV
V
=
y ò ×
y dV
V
=
z ò ×
z dV
V
=
16
The centroid “C” of the Volume segment,
, ,

17. AXIS of SYMMETRY:
It is an axis w.r.t. which for an elementary area on one
side of the axis , there is a corresponding elementary
area on the other side of the axis (the first moment of
these elementary areas about the axis balance each
other)
If an area has an axis of symmetry, then the centroid
must lie on that axis.
If an area has two axes of symmetry, then the centroid
must lie at the point of intersection of these axes.
17

18. For example:
The rectangular shown in
the figure has two axis of
symmetry, X-X and Y-Y.
Therefore intersection of
these two axes gives the
centroid of the rectangle.
Y
da da
D/2
x x
D B
D/2
B/2 B/2
X X
Y
da × x = da × x
Moment of areas,da
about y-axis cancel
each other
da × x + da × x = 0
18

19. AXIS of SYMMETYRY
‘C’ must lie
on the axis
of symmetry
‘C’ must lie at the intersection
of the axes of symmetry
‘C’ must lie on
the axis of
symmetry
19

20. => PRESENTED BY:-
# MIHIR PARESHKUMAR DIXIT. #
# ENROLLMENT NO :- 130810119021.
# M.E. - 3 A. (2014)
#VENUS INTERNATIONAL COLLEGE
OF TECHNOLOGY. #
20