This document discusses fast algorithms for multiplying polynomials. It presents an algorithm that uses complex numbers to multiply polynomials in O(n log n) time, which is faster than the naive O(n^2) algorithm. It does this by converting the polynomial multiplication problem into an equivalent form involving evaluating the polynomials at certain points, which can then be sped up using the Fast Fourier Transform (FFT) algorithm. The FFT algorithm chooses the evaluation points to be complex roots of unity in a way that speeds up the polynomial evaluations.

1. Multiplying Polynomials Fast
Why do we need Complex
Numbers?

2. The Problem
• (an xn + an-1 xn-1+…..+ a0 x0) * (bn xn + bn-1 xn-1+…..+ b0 x0)
• O(n^2) time
– (Σi=0..k ai * bk-i) is coefficient of xk
• Can one do better?

3. Applications
• Where all does a pattern string P appear in a text string
T?
– P 0’s, 1’s and don’t cares.
– T 0’s and 1’s
• Easy in O(|P|*|T|) time
– Can one do better?

4. Conversion to Polynomial
Multiplication
• Treat P and T as polynomials
– T=0101 1 x0 + 0 x1 + 1 x2 + 0 x3
tk-i tk-2 tk-1 tk
– P=01D1 0 x0 + 1 x1 + 0 x2 + 1 x3
1 0 1 0 1 1 0 0 1
• Multiply Prev and T
1 0 0 0 1 0 0
p-i p-1 p-0
– (Σi=0..k previ * tk-i) is coefficient of xk
– (Σi=0..k p|P|-i * tk-i) is coefficient of xk
• >=1 if and only if a 1 in P aligns with a 0 in T when P is placed with end at
tk
– 2 polynomial multiplications suffice to find all matches of P in T

5. Other Applications
• Image Processing At this
location
Slide this mask
all over the
Multiply each bit
bigger one in the mask with
the
corresponding bit
in the image,
sum these up

6. Polynomial Multiplication
An Equivalent Form
• Evaluate each polynomial at 2n+1 distinct x’s
– A(x) = (an xn + an-1 xn-1+…..+ a0 x0) -> A(v0)…..A(v2n)
– B(x) = (bn xn + bn-1 xn-1+…..+ b0 x0) -> B(v0)…..B(v2n)
• A(x) * B(x) -> A(v0)*B(v0)………..A(v2n)*B(v2n)
– Convolution in one domain=Simple multiplication in another
– O(n) time!!!

7. Multi-Point Polynomial Evaluation
• Evaluate A(x) at v0 ……vn
– O(n) time per vi using Horner’s rule
• Problems
– O(n2) time
– Large numbers with n log vi bits

8. Multi-Point Polynomial Evaluation
Speed Up
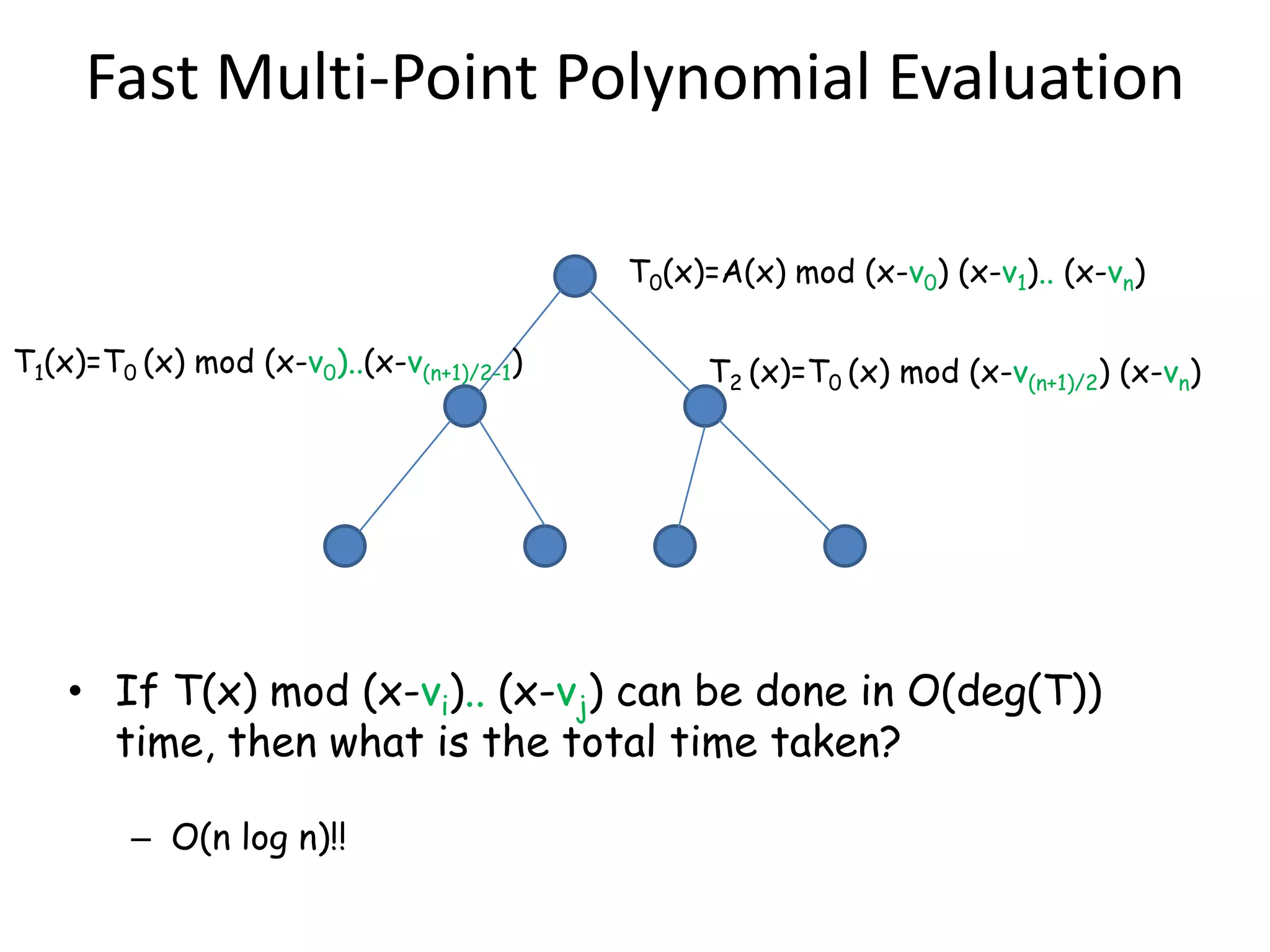
• A(x) mod (x-v)
– A(v)
– O(n) time using high school polynomial division
• A’(x) = A(x) mod (x-v0) (x-v1) [how fast?]
– A’(x) mod (x-v0) = A(v0) [O(1)]
– A’(x) mod (x-v1) = A(v1) [O(1)]
– 2 expensive polynomial divisions could potentially be replaced by 1

9. Fast Multi-Point Polynomial Evaluation
T0(x)=A(x) mod (x-v0) (x-v1).. (x-vn)
T1(x)=T0 (x) mod (x-v0)..(x-v(n+1)/2-1) T2 (x)=T0 (x) mod (x-v(n+1)/2) (x-vn)
• If T(x) mod (x-vi).. (x-vj) can be done in O(deg(T))
time, then what is the total time taken?
– O(n log n)!!

10. Computing T(x) mod (x-v1).. (x-vk)
• High school algorithm
– Time taken: O( deg(T) * k )
– How do we make this faster?
• Stroke of genius
• Can we choose vi’s so (x-v1).. (x-vk) = xk-v?
• Then we get O(deg(T) ) time

11. Choosing vi’s
• When is (x-v1)(x-v2) = x2+v1v2 ?
– v2+v1=0
• When is (x-a)(x+a)(x-b)(x+b) = x4+ a2b2?
– b2-a2=0 => b2=-a2
• => b= sqrt(-1) a
• the 4 numbers are 1 –i -1 i
• alternatively (–i)0 (–i)1 (–i)2 (–i)3

12. Choosing vi’s
• Choose vi to be roots of xn -1
= Cos(2Πk/n) + i Sin(2Πk/n)
= e i 2Πk/n
– Powering just goes around the unit circle
• Computing with log n bits suffices

13. Exercise
• Choose vi to be roots of xn -1
= Cos(2Πk/n) + i Sin(2Πk/n)
= e i 2Πk/n
– Organize these roots so we get polynomials with
just 2 terms in every node of the tree on slide 9
• Assume n+1 is a power of 2

14. Conclusion
• Also called : Fast Fourier Transform
• Complex Numbers are interesting!
• Reality can be explained elegantly only with
complex numbers!!