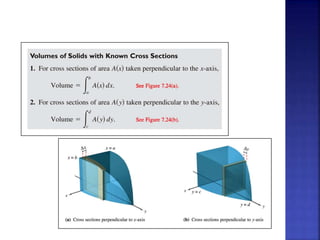
Embed presentation
Download to read offline

![Ex 4 p460 Integrating with Respect to y, Two-Integral case.
Find the volume of the solid formed by revolving the region
bounded by the graphs of y = x2 + 1, y = 0, x= 0 and x = 1 about
the y-axis.
Part of this region will revolve and be washers,
and part will be disks. So the region must be
split up at the level where y=1.
I am revolving about y-axis, so y is being sliced
up as dy. I will need functions in terms of y for
the radii.
In the upper part, the inner radius is
determined by and the outer
radius is still x = 1
1
y x
1 2
2
2 2
0 1
1 [1 1 ]
dy y dy
1 2
0 1
1 [2 ]
dy y dy
3
2
X = 1
1
x y
](https://image.slidesharecdn.com/calc7-2b-120202101948-phpapp02/85/Calc-7-2b-2-320.jpg)


The document provides instructions for calculating the volume of two different solids by revolving regions about axes and integrating with respect to the variable of integration. For the first solid, the region is bounded by y = x^2 + 1, y = 0, x = 0, and x = 1 when revolved about the y-axis. The region is split at y = 1 and the volume is found using disks and washers, integrating from y = 0 to y = 1 and y = 1 to y = 2. For the second solid, the region is bounded by y = 1/2x and y = -1/2x + 1 when revolved about the x-axis. The base

![Ex 4 p460 Integrating with Respect to y, Two-Integral case.
Find the volume of the solid formed by revolving the region
bounded by the graphs of y = x2 + 1, y = 0, x= 0 and x = 1 about
the y-axis.
Part of this region will revolve and be washers,
and part will be disks. So the region must be
split up at the level where y=1.
I am revolving about y-axis, so y is being sliced
up as dy. I will need functions in terms of y for
the radii.
In the upper part, the inner radius is
determined by and the outer
radius is still x = 1
1
y x
1 2
2
2 2
0 1
1 [1 1 ]
dy y dy
1 2
0 1
1 [2 ]
dy y dy
3
2
X = 1
1
x y
](https://image.slidesharecdn.com/calc7-2b-120202101948-phpapp02/85/Calc-7-2b-2-320.jpg)


