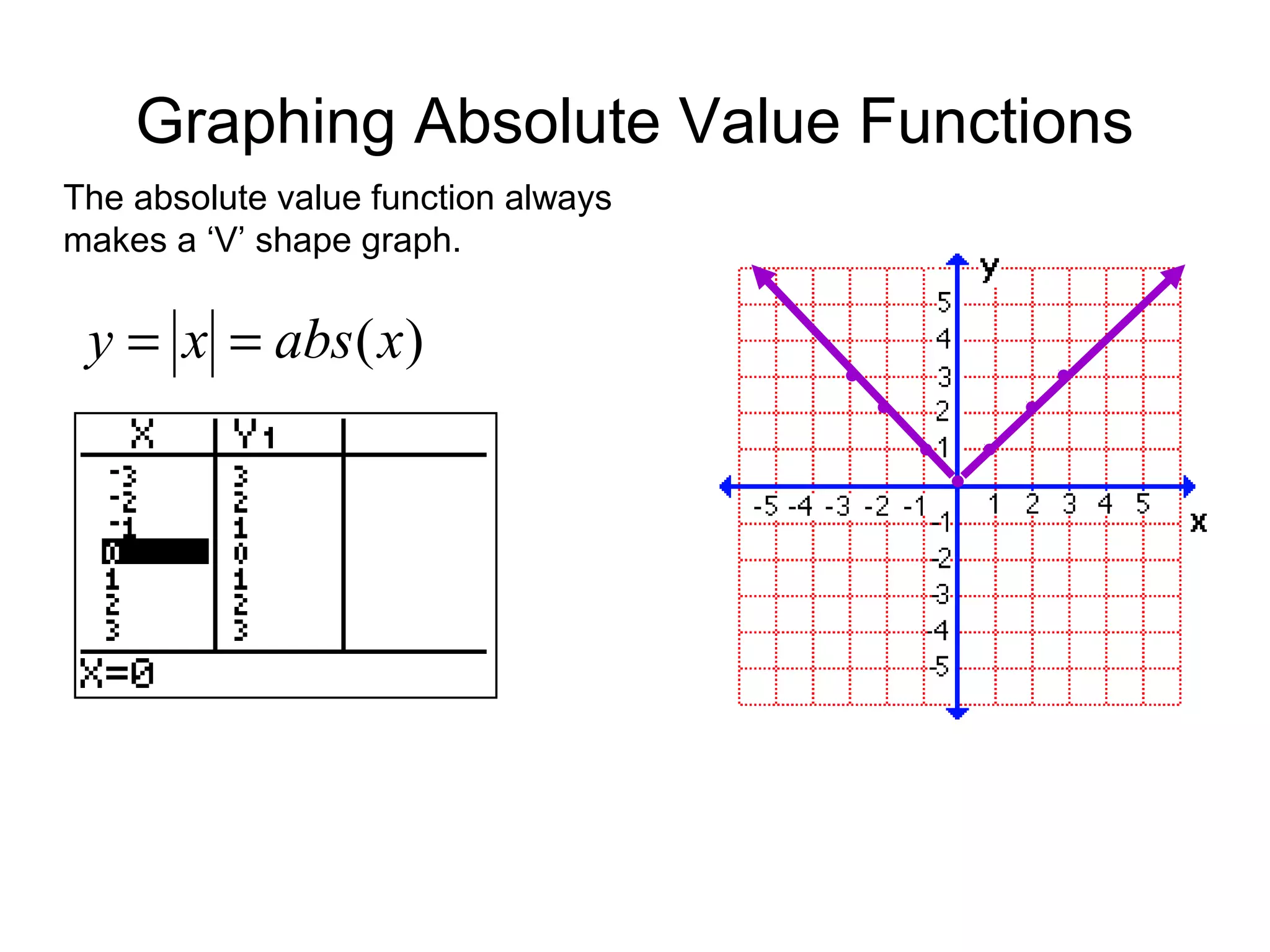
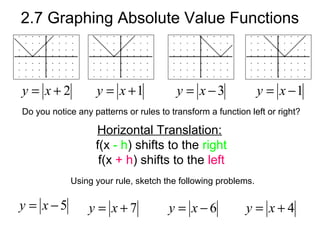
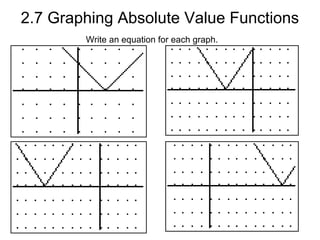
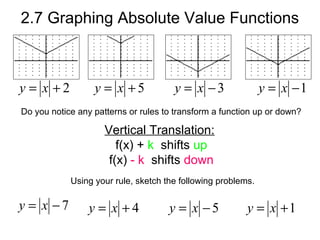
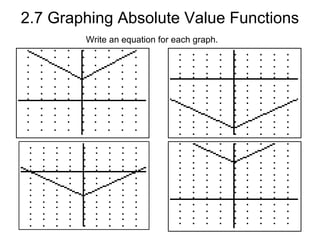
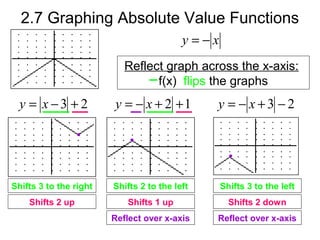
The document discusses graphing absolute value functions. It notes that absolute value functions always form a V-shape graph. It provides the general form of an absolute value function as y = a |x - h| + k, where (h, k) are the coordinates of the vertex and a describes the slope. It explains that horizontal shifts are performed by adding or subtracting h from x and vertical shifts add or subtract k from the function. Reflecting the graph over the x-axis flips it vertically. Examples demonstrate shifting graphs left, right, up, down and reflecting over the x-axis.

1. Graphing Absolute Value Functions
The absolute value function always
makes a ‘V’ shape graph.
)(xabsxy ==

2. Absolute Value
Functions
General Form: y = a | x – h | + k
1. The graph is V-shaped
2. Vertex of the graph: (h, k)
3. a acts as the slope for the right hand side
(the left side is the opposite)

3. 2.7 Graphing Absolute Value Functions
2+= xy 1+= xy 3−= xy 1−= xy
Do you notice any patterns or rules to transform a function left or right?
Using your rule, sketch the following problems.
5−= xy 7+= xy 6−= xy 4+= xy
Horizontal Translation:
f(x - h) shifts to the right
f(x + h) shifts to the left

4. 2.7 Graphing Absolute Value Functions
Write an equation for each graph.

5. 2.7 Graphing Absolute Value Functions
Do you notice any patterns or rules to transform a function up or down?
Using your rule, sketch the following problems.
7−= xy 4+= xy 5−= xy 1+= xy
Vertical Translation:
f(x) + k shifts up
f(x) - k shifts down
2+= xy 5+= xy 3−= xy 1−= xy

6. 2.7 Graphing Absolute Value Functions
Write an equation for each graph.

7. 2.7 Graphing Absolute Value Functions
Reflect graph across the x-axis:
f(x) flips the graphs
xy −=
23 +−= xy
Shifts 3 to the right
Shifts 2 up
12 ++−= xy
Shifts 2 to the left
Shifts 1 up
Reflect over x-axis
Shifts 3 to the left
Shifts 2 down
Reflect over x-axis
23 −+−= xy