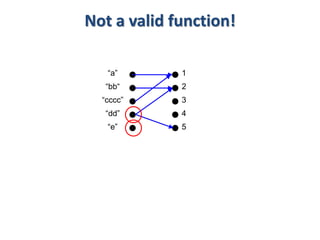
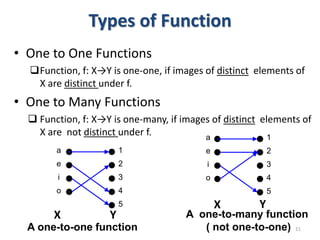
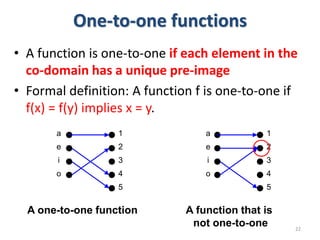
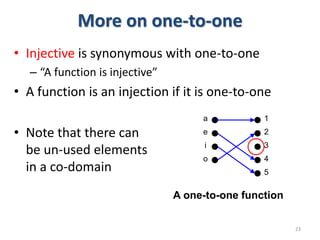
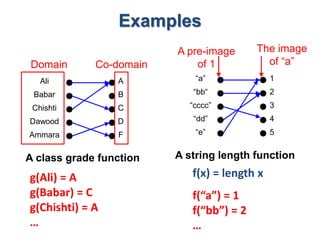
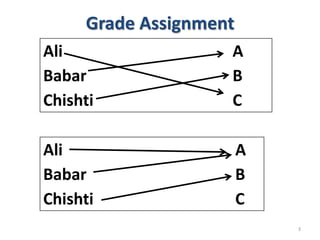
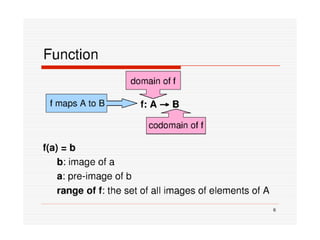
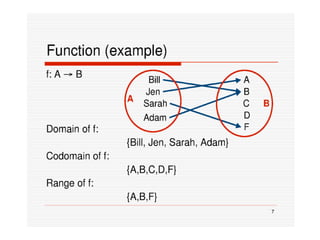
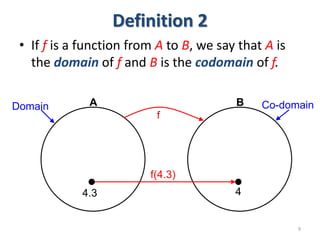
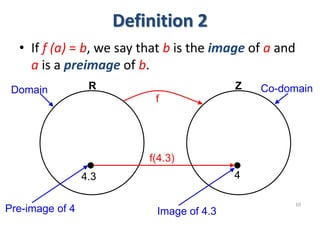
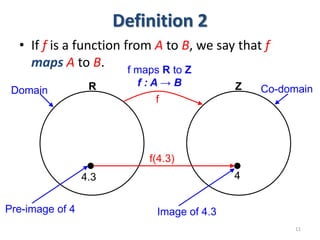
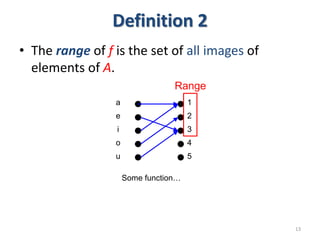
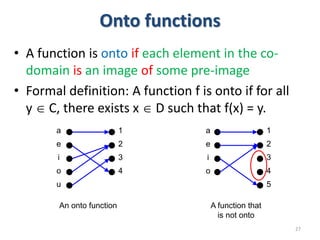
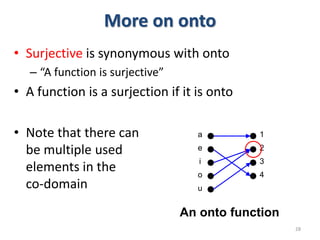
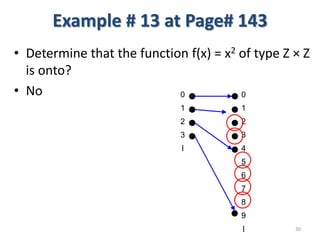
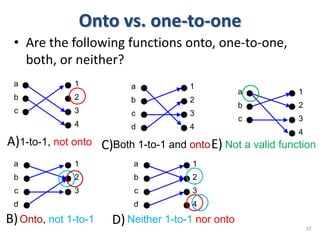
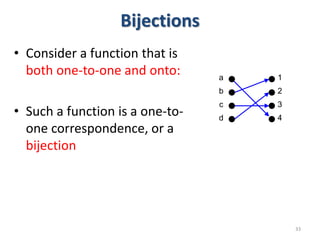
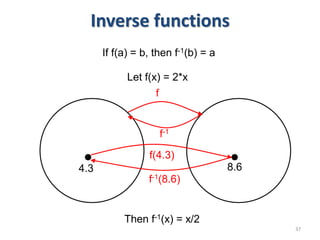
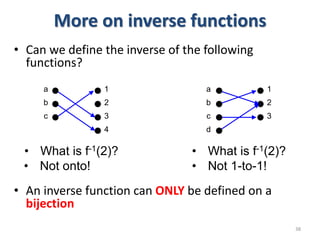
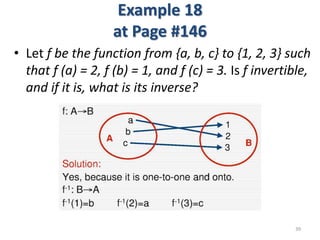
1) The document discusses functions and provides examples of different types of functions including one-to-one functions, onto functions, bijections, and inverse functions. 2) It also gives examples of specifying functions using ordered pairs, formulas, and computer programs. Functions can be added, subtracted, multiplied, and divided. 3) The key aspects of a function are its domain, codomain, and range. A function is one-to-one if each element in the codomain has a unique pre-image, onto if each element in the codomain is the image of some pre-image, and a bijection if it is both one-to-one and onto.

1. Discrete Structures
Functions
Dr. Muhammad Humayoun
Assistant Professor
COMSATS Institute of Computer Science, Lahore.
mhumayoun@ciitlahore.edu.pk
https://sites.google.com/a/ciitlahore.edu.pk/dstruct/
A lot of material is taken from the slides of Dr. Atif and Dr. Mudassir
1

2. Recall the Cartesian Product
• All ordered n-tuples (2 tuples in our example)
• Let S = { Ali, Babar, Chishti } and G = { A, B, C }
• S×G = { (Ali, A), (Ali, B), (Ali, C), (Babar, A), (Babar, B),
(Babar, C), (Chishti , A), (Chishti , B), (Chishti , C) }
–A relation
• The final grades will be a subset of this:
–{ (Ali, C), (babar, B), (Chishti, A) }
2

3. Grade Assignment
Ali A
Babar B
Chishti C
3
Ali A
Babar B
Chishti C

4. Function
• This assignment is an example of a function
• A function is a set of ordered pairs in which each
x-element has only ONE y-element associated
with it
• The concept of a function is extremely important
in mathematics and computer science
4

5. Definition 1
Let A and B be nonempty sets. A function f from A
to B is an assignment of exactly one element of B
to each element of A.
We write f (a) = b if b is the unique element of B
assigned by the function f to the element a of A.
If f is a function from A to B, we write f : A → B.
5

6. Specifying a Function
Many different ways:
• Sometimes we explicitly state the assignments,
as in previous figure
• Often we give a formula, such as f (x) = x + 1, to
define a function
• Other times we use a computer program to
specify a function
6

7. 7

8. 8

9. Definition 2
• If f is a function from A to B, we say that A is
the domain of f and B is the codomain of f.
9
A B
f
4.3 4
Domain Co-domain
f(4.3)

10. Definition 2
• If f (a) = b, we say that b is the image of a and
a is a preimage of b.
10
R Z
f
4.3 4
Domain Co-domain
Pre-image of 4 Image of 4.3
f(4.3)

11. Definition 2
• If f is a function from A to B, we say that f
maps A to B.
11
R Z
f
4.3 4
Domain Co-domain
Pre-image of 4 Image of 4.3
f maps R to Z
f : A → B
f(4.3)

12. Examples
1
2
3
4
5
“a”
“bb“
“cccc”
“dd”
“e”
A string length function
A
B
C
D
F
Ali
Babar
Chishti
Dawood
Ammara
A class grade function
Domain Co-domain
A pre-image
of 1
The image
of “a”
g(Ali) = A
g(Babar) = C
g(Chishti) = A
…
f(x) = length x
f(“a”) = 1
f(“bb”) = 2
…

13. Definition 2
• The range of f is the set of all images of
elements of A.
13
1
2
3
4
5
a
e
i
o
u
Some function…
Range

14. Not a valid function!
1
2
3
4
5
“a”
“bb“
“cccc”
“dd”
“e”

15. EXAMPLE 1
at Page# 140
• What are the domain, co-domain, and range of the function
that assigns grades to students?
• Let G be the function that assigns a grade to a student in our
discrete mathematics class.
• Domain of G is {Adams, Chou, Goodfriend, Rodriguez, Stevens},
• Co-domain is the set {A,B,C,D, F}.
• Range of G is the set {A,B,C, F},
15

16. EXAMPLE 2
at Page# 140
• Let R be the relation with ordered pairs (Abdul, 22), (Brenda, 24),
(Carla, 21), (Desire, 22), (Eddie, 24), and (Felicia, 22). Here each
pair consists of a graduate student and this student’s age. Specify
a function determined by this relation.
16
22
24
21
Abdul
Brenda
Carla
Desire
Eddie
Felicia
If f is a function specified by R, then f (Abdul ) = 22,
f (Brenda) = 24, f (Carla) = 21, f (Desire) = 22,
f (Eddie) = 24, and f (Felicia) = 22. (Here, f (x) is the
age of x, where x is a student.)
Domain: set {Abdul, Brenda, Carla, Desire, Eddie, Felicia}.
Co-domain: set {21, 22, 24}.
Range: set {21, 22, 24}.

17. Example#4 at Page 40
• Let f : Z → Z
assign the square of an integer to this integer
• What is f (x) =?
– f(x) = x2
• What is domain of f ?
– Set of all integers
• What is codomain of f ?
– Set of all integers
• What is the range of f ?
– {0, 1, 4, 9, . . . }. All integers that are perfect squares
17

18. Function arithmetic
• Just as we are able to add (+), subtract (-), multiply
(×), and divide (÷) two or more numbers, we are
able to + , - , × , and ÷ two or more functions
• Let f and g be functions from A to R. Then f + g, f –
g, f × g and f/g are also functions from A to R
defined for all x ∈ A by:
• (f + g)(x) = f(x) + g(x)
• (f - g)(x) = f(x) - g(x)
• (f g)(x) = f (x)g(x) (f g)(x) Ξ (f × g)(x)
• (f/g)(x) = f(x)/g(x) given that g(x)≠0
18

19. Example 6 at Page# 141
• Let f1 and g be functions from R to R such that:
• f(x) = x2 //square function
• g (x) = x − x2 //some other function
• What are the functions f + g and f g?
• f + g = (f + g)(x) = f (x) + g(x) = x2 + (x − x2) = x
• (f g) = (f g)(x) = f(x)g(x) = x2(x − x2) = x3 − x4
• What is f(x)+g(x) and f+g(x) if x=2?
• f(2)=4, g(2)=-2; f(2)+g(2) = 4-2=2
• f+g(2) = 2 19

20. Another Example
• Let f and g be functions from R to R such that:
• f (x) = 3x+2
• g (x) = -2x + 1
• What is the function f g?
• f g= (f g)(x) = f (x)g(x) = (3x+2)(-2x+1) = -6x2- x +2
Let x = -1, what is f(-1).g(-1) and (f g)(-1)?
20
f (-1) = 3(-1) + 2 = -1
g(-1) = -2(-1) + 1= 3
f(-1) g(-1) = -1×3 = -3
(f g) (-1) = -6(-1)2 – (-1) + 2
= -6+1+2
= -3

21. Types of Function
• One to One Functions
Function, f: X→Y is one-one, if images of distinct elements of
X are distinct under f.
• One to Many Functions
 Function, f: X→Y is one-many, if images of distinct elements of
X are not distinct under f.
21
1
2
3
4
5
a
e
i
o
A one-to-one function
1
2
3
4
5
a
e
i
o
A one-to-many function
( not one-to-one)
X Y
X Y

22. One-to-one functions
• A function is one-to-one if each element in the
co-domain has a unique pre-image
• Formal definition: A function f is one-to-one if
f(x) = f(y) implies x = y.
22
1
2
3
4
5
a
e
i
o
A one-to-one function
1
2
3
4
5
a
e
i
o
A function that is
not one-to-one

23. More on one-to-one
• Injective is synonymous with one-to-one
– “A function is injective”
• A function is an injection if it is one-to-one
• Note that there can
be un-used elements
in a co-domain
23
1
2
3
4
5
a
e
i
o
A one-to-one function

24. Example# 9 at Page# 142
• Determine that the function f(x) = x2 of type
from (the set of integers to the set of
integers is) Z × Z is one-to-one.
• 0 -> 0
• 1 -> 1 -1 -> 1
• 2 -> 4 -2 -> 4
• 3 -> 9 -3 -> 9
• 10 -> 100 -10 -> 100
• The function f (x) = x2 is not one-to-one
24

25. Example# 10 at Page# 142
• Determine whether the function f (x) = x + 1 from
the set of real numbers to itself is one-to one.
• 0 -> 1
• 1 -> 2
• 2 -> 3
• 3 -> 4
• 10 -> 11
• The function f (x) = x + 1 is a one-to-one function.
25

26. • Next Class
26

27. Onto functions
• A function is onto if each element in the co-
domain is an image of some pre-image
• Formal definition: A function f is onto if for all
y  C, there exists x  D such that f(x) = y.
27
1
2
3
4
5
a
e
i
o
A function that
is not onto
1
2
3
4
a
e
i
o
u
An onto function

28. More on onto
• Surjective is synonymous with onto
– “A function is surjective”
• A function is a surjection if it is onto
• Note that there can
be multiple used
elements in the
co-domain
28
1
2
3
4
a
e
i
o
u
An onto function

29. Example # 12 at Page# 143
• Let f be the function from {a, b, c, d} to {1, 2, 3}
defined by f (a) = 3, f (b) = 2, f (c) = 1, and f (d) =
3. Is f an onto function?
• f (a) = 3
• f (b) = 2
• f (c) = 1
• f (d) = 3
• Yes, f is an onto function
29

30. Example # 13 at Page# 143
• Determine that the function f(x) = x2 of type Z × Z
is onto?
• No
30
0
1
2
3
4
5
6
7
8
9
⁞
0
1
2
3
⁞

31. Example # 14 at Page# 143
• Is the function f (x) = x + 1 from the set of
integers to the set of integers onto?
• 0 -> 1
• 1 -> 2
• 2 -> 3
• 3 -> 4
• 10 -> 11
• The function f (x) = x + 1 is a onto function.
31

32. Onto vs. one-to-one
• Are the following functions onto, one-to-one,
both, or neither?
32
1
2
3
4
a
b
c
1
2
3
a
b
c
d
1
2
3
4
a
b
c
d
1
2
3
4
a
b
c
d
1
2
3
4
a
b
c
1-to-1, not onto
Onto, not 1-to-1
Both 1-to-1 and onto Not a valid function
Neither 1-to-1 nor onto
A)
B)
C)
D)
E)

33. Bijections
• Consider a function that is
both one-to-one and onto:
• Such a function is a one-to-
one correspondence, or a
bijection
33
1
2
3
4
a
b
c
d

34. Example # 16 at Page# 144
• Let f be the function from {a, b, c, d} to {1, 2, 3, 4}
with f (a) = 4, f (b) = 2, f (c) = 1, and f (d) = 3. Is f a
bijection?
• f (a) = 3
• f (b) = 2
• f (c) = 1
• f (d) = 3
• Yes, f is an onto function and one to one function.
Hence, Bijection.
34

35. Identity functions
• A function such that the image and the pre-
image are ALWAYS equal
• f(x) = 1*x
• f(x) = x + 0
• The domain and the co-domain must be the
same set
35

36. Inverse of a Function
• For bijections f:AB, there exists an inverse of f,
written f 1:BA, which is the unique function
such that:
• If the inverse function of f exists, f is called
invertible.
• The function is not invertible if it is not bijection.
36
I
f
f 


1

37. Inverse functions
37
f
4.3 8.6
Let f(x) = 2*x
f-1
f(4.3)
f-1(8.6)
Then f-1(x) = x/2
If f(a) = b, then f-1(b) = a

38. More on inverse functions
• Can we define the inverse of the following
functions?
• An inverse function can ONLY be defined on a
bijection
38
1
2
3
4
a
b
c
1
2
3
a
b
c
d
• What is f-1(2)?
• Not onto!
• What is f-1(2)?
• Not 1-to-1!

39. Example 18
at Page #146
• Let f be the function from {a, b, c} to {1, 2, 3} such
that f (a) = 2, f (b) = 1, and f (c) = 3. Is f invertible,
and if it is, what is its inverse?
39

40. Example 19
at Page #146
• Let f : Z → Z be such that f (x) = x + 1. Is f invertible, and if
it is, what is its inverse?
• 0 -> 1
• 1 -> 2
• 2 -> 3
• 3 -> 4
• 10 -> 11
• The function f (x) = x + 1 is a one-to-one and onto function, therefore, f
is invertible.
• Suppose That y=x+1
• x= y-1
• f-1 (y)=y-1
40

41. Example 20
at Page #146
• Let f be the function from R to R with f (x) = X2, Is f
invertible?
• 0 -> 0
• 1 -> 1 -1 -> 1
• 2 -> 4 -2 -> 4
• 3 -> 9 -3 -> 9
• 10 -> 100 -10 -> 100
• The function f (x) = x2 is not one to one
• Therefore, Not Invertible.
41

42. Example 21
at Page #146
• Show that if we restrict the function f (x) = X2 in Example 20 to a
function from the set of all nonnegative real numbers to the set of
all nonnegative real numbers, then f is invertible.
42

43. Compositions of functions
43
g f
f ○ g
g(1) f(5)
(f ○ g)(1)
g(1)=5
f(g(1))=13
1
R R R
Let f(x) = 2x+3 Let g(x) = 3x+2
f(g(x)) = 2(3x+2)+3 = 6x+7

44. Compositions of functions
Does f(g(x)) = g(f(x))?
Let f(x) = 2x+3 Let g(x) = 3x+2
f(g(x)) = 2(3x+2)+3 = 6x+7
g(f(x)) = 3(2x+3)+2 = 6x+11
Function composition is not commutative!
44
Not equal!

45. Proving a function is 1-1
https://www.youtube.com/watch?v=bjATxNZp4GI
• A function is said to be 1-1 if whenever F(x)=f(y)
then x=y, i.e., for same input, output is also same.
1/30/2023

46. Proving a function is onto
https://www.youtube.com/watch?v=Uzlj6N5OYcM
1/30/2023

47. Example 22
at Page# 147
• Let g be the function from the set {a, b, c} to itself such that g(a) =
b, g(b) = c, and g(c) = a. Let f be the function from the set {a, b, c}
to the set {1, 2, 3} such that f (a) = 3, f (b) = 2, and f (c) = 1. What
is the composition of f and g, and what is the composition of g
and f ?
• Solution:
 The composition f ◦ g is defined by (f ◦ g)(a) = f (g(a)) = f (b) = 2,
 (f ◦ g) (b) = f (g(b)) = f (c) = 1,
 and (f ◦ g)(c) = f (g(c)) = f (a) = 3.
• Note that g ◦ f is not defined, because the range of f is not a
subset of the domain of g.
47

48. Example 23
at Page# 147
• Let f and g be the functions from the set of integers to the set of
integers defined by f (x) = 2x + 3 and g(x) = 3x + 2. What is the
composition of f and g? What is the composition of g and f ?
• Solution:
• Both the compositions f ◦ g and g ◦ f are defined. Moreover,
• (f ◦ g)(x) = f (g(x)) = f (3x + 2) = 2(3x + 2) + 3 = 6x + 7
and
• (g ◦ f )(x) = g(f (x)) = g(2x + 3) = 3(2x + 3) + 2 = 6x + 11.
48

49. Proving Function problems

50. Defining Functions
• Square Function:
F: Z→Z
F(x)= x*x
• Sum Function:
Sum: R→R→R
Sum (x,y)= x+y
• Abs Function:
Abs: Z→Z
 │x│=
50

51. Defining Functions …
• abs function:
– 𝑎𝑏𝑠 ∶ 𝑍 ⇒ 𝑍
– 𝑎𝑏𝑠(𝑥) =
−𝑥, if 𝑥 < 0
𝑥, otherwise 𝑥 ≥ 0
.
• Is the following a valid absolute function?
– 𝑎𝑏𝑠 ∶ 𝑍 ⇒ 𝑍
– 𝑎𝑏𝑠(𝑥) =
−𝑥, if 𝑥 < 0
𝑥, otherwise 𝑥 > 0
.
51

52. Defining Recursive Function
• Factorial of n = n× (n-1) ×(n-2)×…. ×1
• Factorial of 0 = 1
• Factorial of 1 = 1
• 𝑓𝑎𝑐𝑡: 𝑍 ⇒ 𝑍
• 𝑓𝑎𝑐𝑡(𝑥) =
1, if 𝑥 ≤ 0
𝑥 × 𝑓𝑎𝑐𝑡 𝑥 − 1 , 𝑖𝑓 𝑥 > 0.
52

53. Another Example
• Suppose that 𝑓 is defined recursively by
• 𝑓(0) = 100,
• 𝑓(𝑥 + 1) = 𝑓(𝑥) + 3
• Find 𝑓 2 .
• To find f(2), we also need to find f(1):
• f(1) = f(0) + 3 = 100 + 3 = 103
• f(2) = f(1) + 3 = 103 + 3 = 106
• What is f(5)?
• F(5) = f(4)+3 = [f(3)+3] +3 = [[f(2)+3]+3]+3
• = [[[f(1)+3]+3]+3]+3 = [[[[f(0)+3]+3]+3]+3]+3 53

54. 54