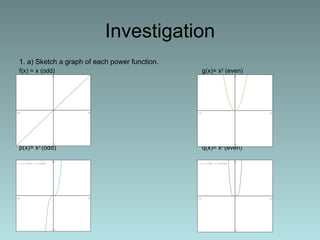
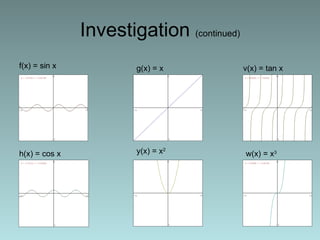
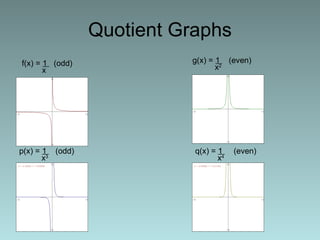
The document discusses products and quotients of functions. It defines products as multiplication and quotients as division. It provides the formulas for determining the product and quotient of functions. It then investigates properties of products and quotients through examples of combining different types of functions - even, odd, and combinations of even and odd. It explores how the symmetry (even or odd) of the combined function relates to the symmetries of the individual factor functions. Examples are provided to illustrate these properties.

1. Introduction: Products and Quotients of Functions

2. Definitions Products: The result of multiplication e.g. 2 x 2= 4 Quotients: The result of division e.g.

3. Equations The formula for determining the product of a function is: y= f( x )g( x ) The formula for determining the quotient of a function is: y= f(x) g(x)

4. Investigation 1. a) Sketch a graph of each power function. f(x) = x (odd) g(x)= x 2 (even) p(x)= x 3 (odd) q(x)= x 4 (even)

5. 2. a) f(x)g(x) = px b) f(x)p(x) = q(x) x(x 2 ) = x 3 x(x 3 ) = x 4 L.S = R.S x 4 = x 4 L.S = R.S c) f(x)f(x) = g(x) d) (g(x)) 2 = q(x) x(x) = x 2 (x 2 ) 2 = x 4 L.S = R.S L.S= R.S Investigation (continued)

6. Investigation (continued) 3. q(x) = x 4 (even) g(x) = x 2 (g(x)) 2 = q(x) g(x) = x 2 (even) f(x) = x (odd) f(x)f(x) = g(x) q(x) = x 4 (even) f(x) = x (odd) p(x) = x 3 (odd) f(x)p(x) = q(x) p(x) = x 3 (odd) f(x) = x (odd) g(x) = x 2 (even) f(x)g(x) = p(x) Symmetry of Product Function Symmetry of Factor Functions Identity

7. Investigation (continued) 4. a) When a combined function consists of two even functions, the product will be even. b) When a combined function consists of two odd functions, the product will be even c) When a combined function consists of an even function and an odd function, the product will be odd.

8. Investigation (continued) f(x) = sin x h(x) = cos x g(x) = x y(x) = x 2 v(x) = tan x w(x) = x 3

9. Quotient Graphs f(x) = 1 (odd) x g(x) = 1 (even) x 2 p(x) = 1 (odd) x 3 q(x) = 1 (even) x 4

10. Quotients of Functions When a combined function consists of two even functions, the quotient will be odd. When a combined function consists of two odd functions, the quotient will be even When a combined function consists of an even function and an odd function, the product will be odd.

11. Purpose Determines the revenue for sports games (i.e. baseball) Helps in economic statistics (i.e. amount of food for a population)

12. Purpose (continued.) Able to predict the chance of someone asking someone else on a date