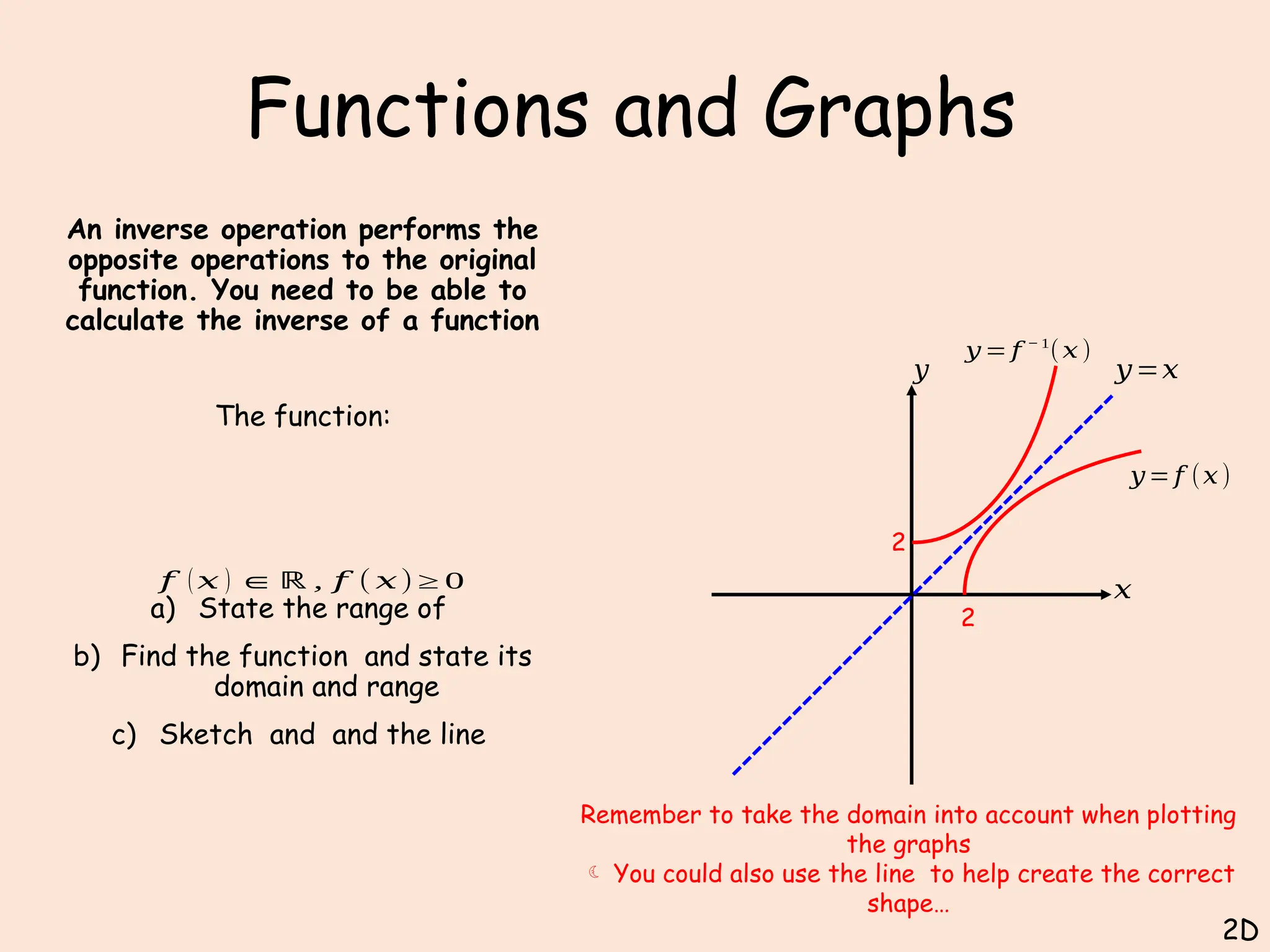
The document covers functions and graphs, focusing on the modulus function, mapping diagrams, and function properties such as one-to-one and many-to-one relationships. It includes examples of solving equations involving composite functions, graph sketching, and determining the domain and range of various functions. The material is structured to aid understanding through practical exercises and teaching points.