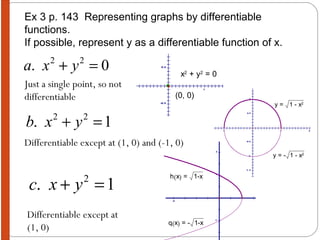
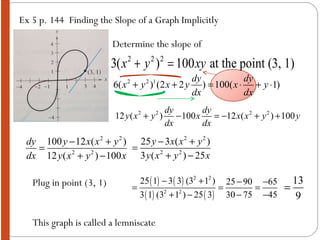
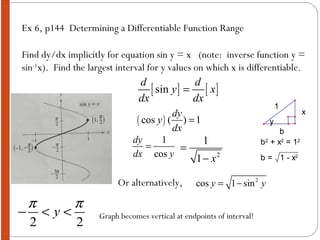
The document discusses implicit differentiation. It explains that implicit differentiation is used when an equation is written implicitly and y cannot be isolated or separated out. The key steps for implicit differentiation are: 1) differentiate both sides of the equation with respect to x, 2) collect all terms involving dy/dx on one side, and 3) solve for dy/dx. Several examples are provided to illustrate implicit differentiation and finding the slope of a graph implicitly using dy/dx. Guidelines and exercises for students to practice implicit differentiation are also included.

1. What do you do when you can’t separate out y? 2.5 Implicit Differentiation

2. Up to now we have seen most equations in explicit form – that is, y in terms of x, like y = 2x 6 -5 (solved for y alone) Now we will work with equations written implicitly, like xy=8. This is the implicit form; it can be rewritten explicitly as y = 8/x Sometimes we can isolate y. Sometimes we can’t! For example, x 2 + 2y 3 + 4y = 2. So we will learn how to implicitly differentiate to handle any situation. When we find dy/dx, we are differentiating with respect to x. Anytime we see a term with x alone, we differentiate as usual. Whenever we differentiate a term involving y, we must apply the Chain Rule, because you are assuming there is some function where y could be written implicitly.

3. When we find dy/dx, we are differentiating with respect to x. Anytime we see a term with x alone, we differentiate as usual. Whenever we differentiate a term involving y, we must apply the Chain Rule, because you are assuming there is some function where y could be written implicitly. Ex 1 p. 141 Differentiating with Respect to x Variables agree: Use simple power rule Variables disagree: Use Chain Rule Product Rule,Chain

4. Guidelines for Implicit Differentiation Differentiate both sides of the equation with respect to x. Collect all terms involving dy/dx on the left side of the equation and move all other terms to the right side of the equation. Factor dy/dx out of the left side of equation Solve for dy/dx Results can be a function in both x and y

5. Ex 2 p. 142 Find dy/dx given that y 3 + y 2 – 5y – x 2 = -4 Solution Differentiate both sides of equation with respect to x. Collect dy/dx terms on one side, rest on other Factor out dy/dx 4. Solve for dy/dx

6. Input y = t, y=t for Play around with window values until you get graph shown. Would you like to see what this graph looks like?

7. Ex 3 p. 143 Representing graphs by differentiable functions. If possible, represent y as a differentiable function of x. Just a single point, so not differentiable Differentiable except at (1, 0) and (-1, 0) Differentiable except at (1, 0)

8. Ex 4 p.143 Finding the Slope of a Graph Implicitly Determine the slope of the tangent line to the graph of Differentiate with respect to x Get dy/dx terms alone, then solve for dy/dx Substitute x and y from point of tangency and simplify. If you want to do it the hard way, solve original equation for y and differentiate that.

9. Ex 5 p. 144 Finding the Slope of a Graph Implicitly Determine the slope of Plug in point (3, 1) This graph is called a lemniscate

10. Ex 6, p144 Determining a Differentiable Function Range Find dy/dx implicitly for equation sin y = x (note: inverse function y = sin -1 x). Find the largest interval for y values on which x is differentiable. Or alternatively, Graph becomes vertical at endpoints of interval!

11. 2.5a p. 146 #1-16 all, 21,23,25