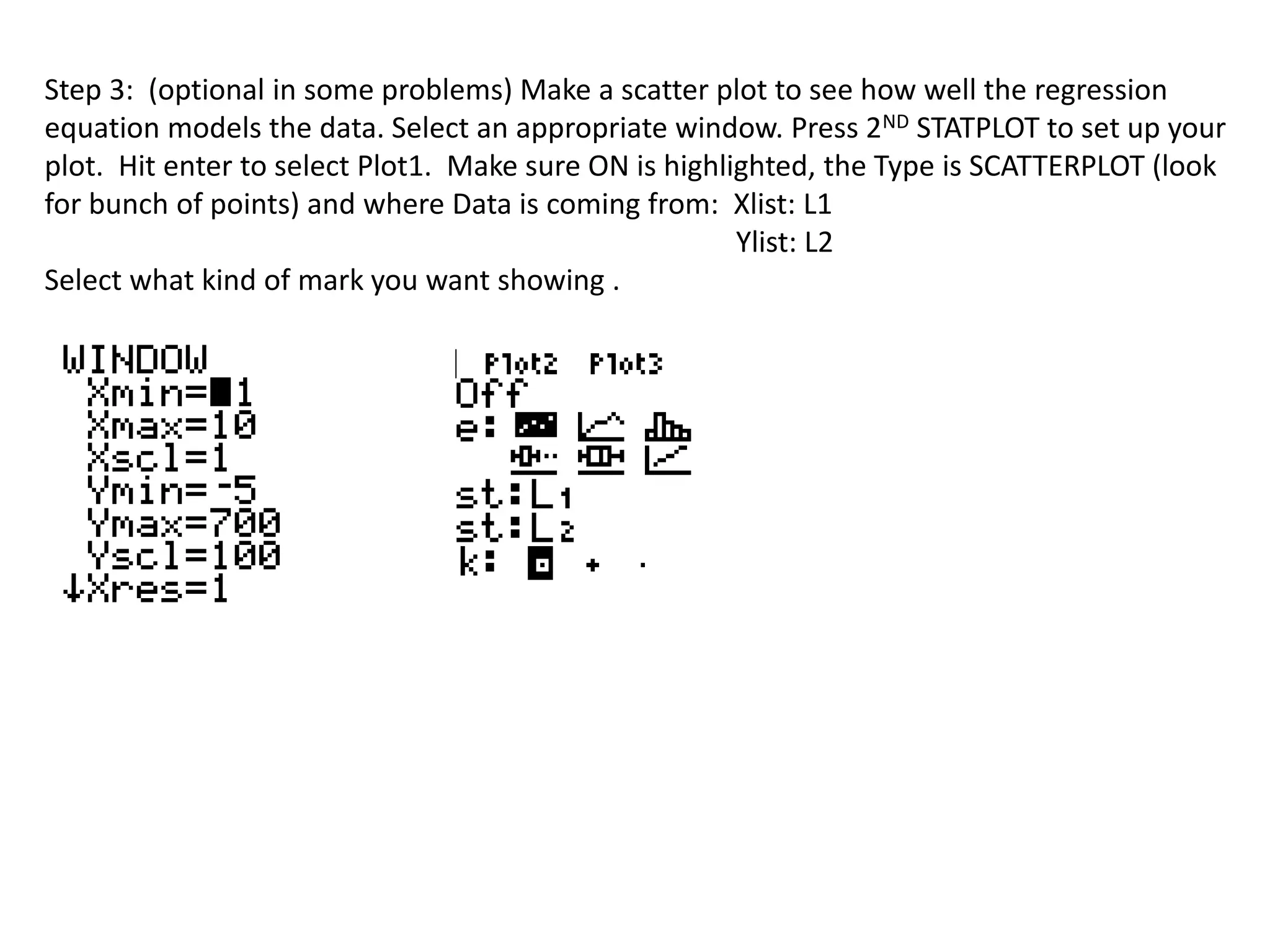
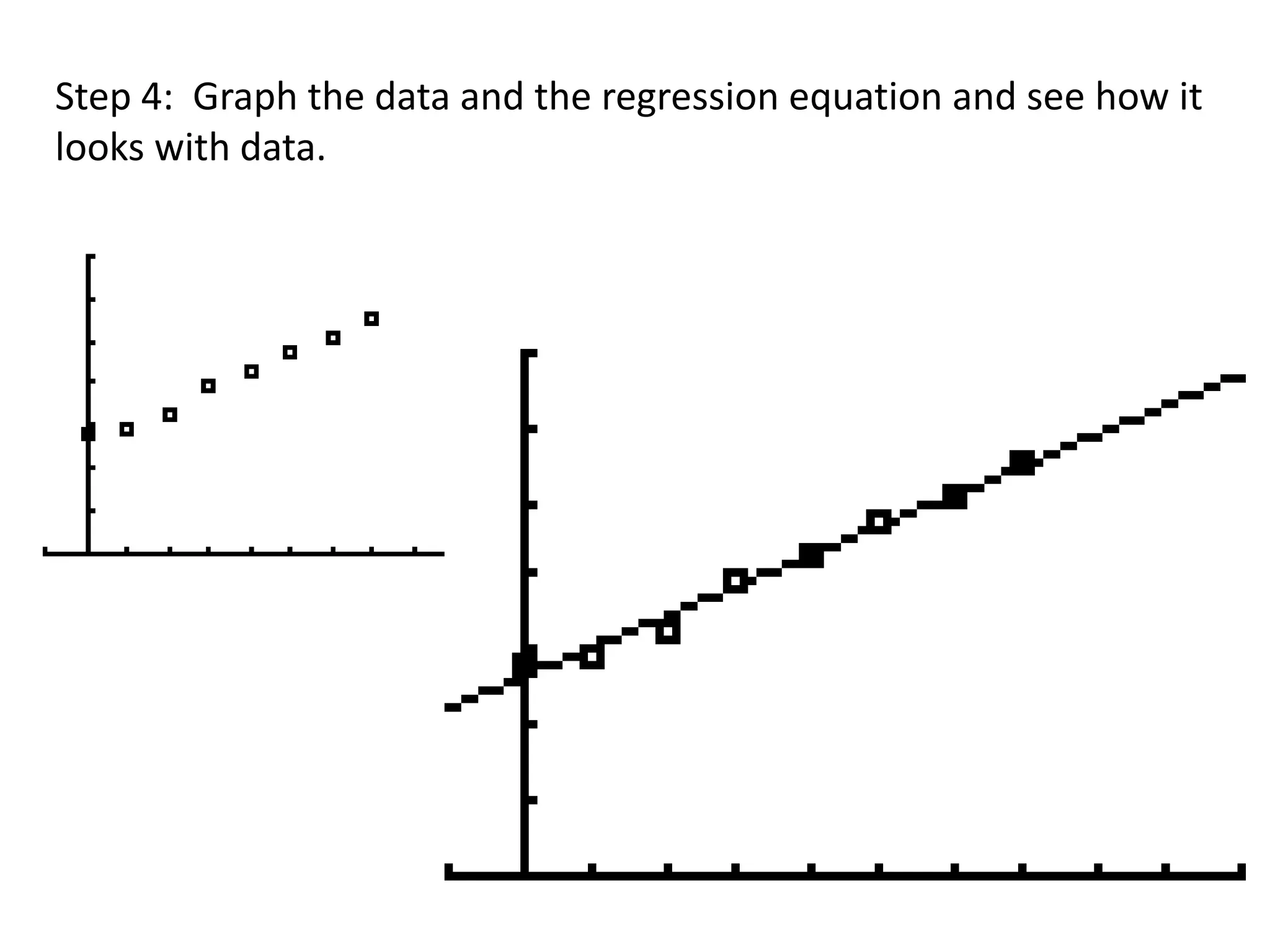
This document provides instructions for using a graphing calculator to perform linear regression on a dataset and find the line of best fit. It describes entering paired x and y data values into separate lists, using the LinReg(ax+b) function to determine the regression equation, optionally creating a scatter plot of the original data and regression line, and using the line equation to forecast values. As an example, it analyzes a dataset of alternative-fueled vehicles in the US from 1997 to predict the number in 2014.

1. 2.6 Lines of Best Fit
Using linear regression features on
graphing calculators.

2. Step 1: Enter the data into two lists. Press STAT, EDIT and in the
L1 column, enter all the x-values from the ordered pairs. In the
L2 column, enter all the y-values from the ordered pairs
Example: The table shows the number y (in thousands) of
alternative-fueled vehicles in the US, x years after 1997.
Approximate the line of best fit by using a calculator.
x 0 1 2 3 4 5 6 7
y 280 295 322 395 425 471 511 548
Another way to enter data is from the main screen; use the
curly brackets (above parentheses) and input each x-value
list with commas in between, store to L1, then do the same
for y-values, store to L2.

3. Step 2: Find an equation of best fitting (linear regression) line.
Press STAT, choose CALC, and then LinReg(ax + b).
Your screen should look like this:
OR If this one, you might need to make
sure it is using L1 and L2 by
inputting after this command
Select Calculate and up will come this screen:
Write down equation. To graph, you
also could have stored this equation in
the previous step.
If your correlation coefficient doesn’t show up, in CATALOG,
select DiagnosticOn.

4. Step 3: (optional in some problems) Make a scatter plot to see how well the regression
equation models the data. Select an appropriate window. Press 2ND STATPLOT to set up your
plot. Hit enter to select Plot1. Make sure ON is highlighted, the Type is SCATTERPLOT (look
for bunch of points) and where Data is coming from: Xlist: L1
Ylist: L2
Select what kind of mark you want showing .

5. Step 4: Graph the data and the regression equation and see how it
looks with data.

6. You can use this Line of BEST FIT to predict values in regions
where you don’t have data. This is called Forecasting , and is
used extensively in business and scientific applications
For example, use the equation in our example to
predict how many alternative-fueled cars there are in
2014.
Solution: Since t = 0 represented 1997, and 2014
represents t = 17, we would take our equation and
input t = 17
You could do this with trace, but might need to change
your window to include x = 17. Make sure you are
paying attention to which graph you are tracing on.
If x = 17, y = 957.6, which is in thousands of cars.

7. HOW DID WE DO?