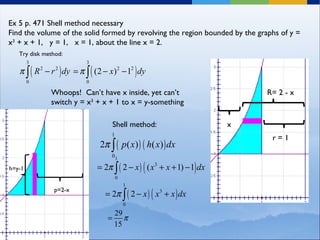
The document provides examples of using different integration methods to solve for the volume of solids formed by rotating regions bounded by graphs about an axis. It gives an example problem of finding the volume of the solid formed by rotating the region bounded by the graphs y = x^3 + x + 1, y = 1, x = 1 about the line x = 2, initially attempting the shell method but realizing the disk method is more suitable. It also lists practice problems from the textbook for quiz on Thursday.

1. Just a few more examples -

2. Ex 5 p. 471 Shell method necessary Find the volume of the solid formed by revolving the region bounded by the graphs of y = x 3 + x + 1, y = 1, x = 1, about the line x = 2. r = 1 R= 2 - x Whoops! Can’t have x inside, yet can’t switch y = x 3 + x + 1 to x = y-something Try disk method: x Shell method: h=y-1 p=2-x

3. http://youtu.be/CiXME1u-oyU 7.3b p. 472/ 21-29 odd, 31-33. 41, 43 QUIZ 7.3 Thursday, Feb 9