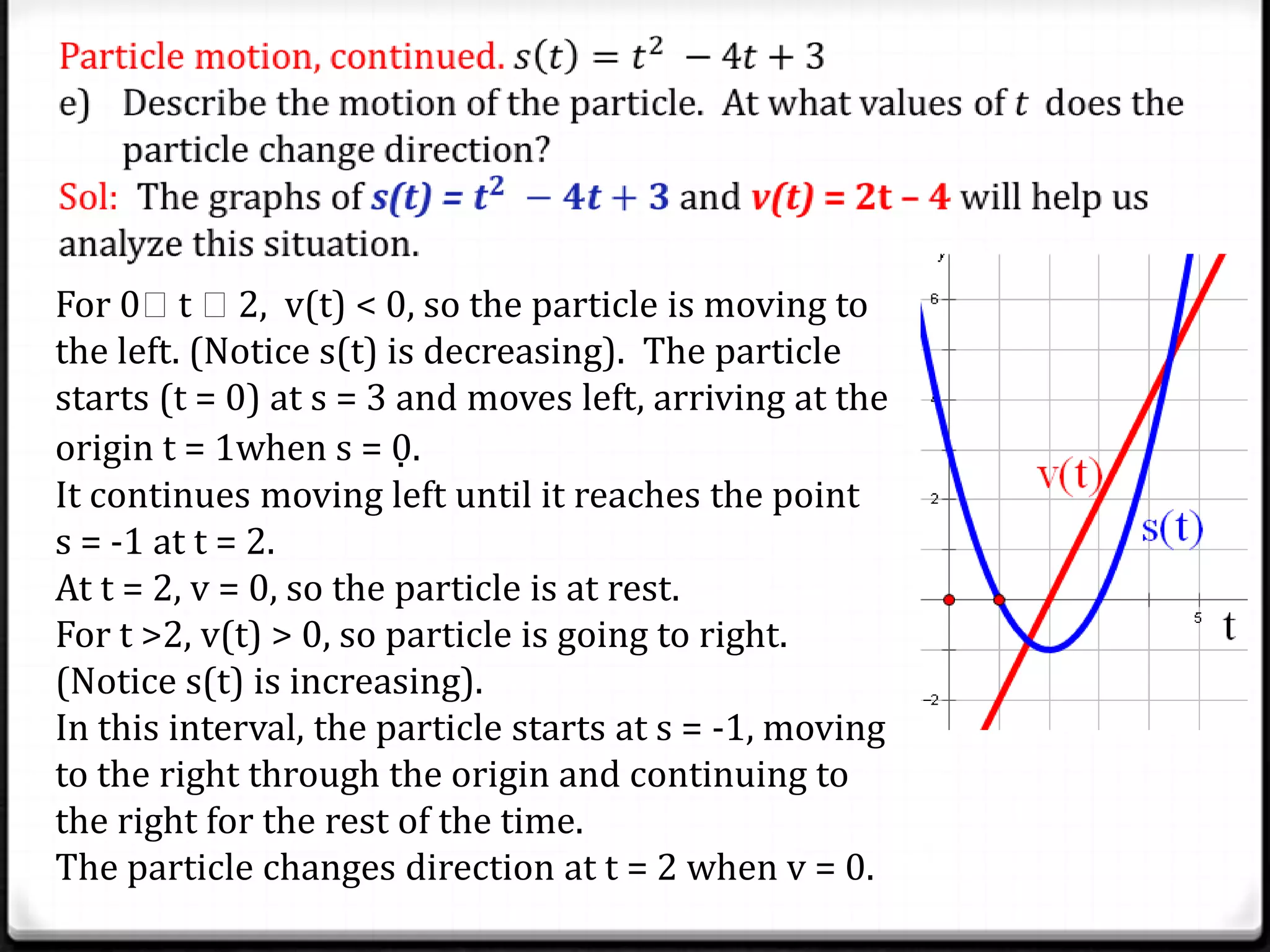
This document discusses key concepts relating to particle motion including position, velocity, and acceleration functions. It provides examples of using the derivative of the position function to find velocity and acceleration. Instantaneous velocity is the derivative of position and

2. The position function (usually called s)
relates position to time.
You might be familiar with
s(t) = -16t2 + v0t + s0
from physics or even algebra 2
This function is used when distance is
measured in feet and v0 is a fancy way of
writing “velocity at time zero, or initial
velocity” and s0 is a fancy way of writing
“position at time zero, or initial position”.

3. Let’s look at s(t) = -16t2 - 30t + 150
Velocity to start is 30 ft/sec (someone
pushed you!), you are falling from a cliff 150
feet high, and you want to know your
position at different times.
s(0) = ? s(1) = ? s(2) = ?
How long till you splat on the ground?
s(0) = 150 ft
s(1) = -16 - 30 + 150 = 104 ft
s(2) = -64 - 60 + 150 =36 ft
Hitting the ground means
position from the ground is 0, so
solve
2
0 16 30 150t t
t=2.26 or -4.14 seconds

4. Change in Distance
Average velocity=
Change in Time
s
t
Distance
Rate=
Time
Ex. 9 p. 113
If a billiard ball is dropped from a height of 100 feet its position is given by
s(t) = -16t2 +100.
Find the average velocity over the following intervals.
a. [1, 2]
b. [1, 1.5]
c. [1, 1.1]
a. Δs = s(2) – s(1) = 36 – 84 = -48 avg vel = -48/1 = -48 ft/sec
b. Δs = s(1.5) – s(1) = 64 – 84 = -20 avg vel = -20/.5= -40 ft/sec
c. Δs = s(1.1) – s(1) = 80.64 – 84 = -3.36 avg vel = -3.36/.1= -33.6 ft/sec
Note that the average velocities are negative, indicating downward movement

5. If you want to find instantaneous velocity at a moment
of time, you would want to calculate the average velocity as
the change in time got smaller and smaller. In other
words, find the rate of change (slope) of the position function
at time t. Sounds like a derivative idea!
0
( ) ( )
( ) lim '( )
t
s t t s t
v t s t
t
The velocity function is the derivative of the position function!
Acceleration is the derivative of velocity with respect to
time, so 2
2
( ) ( )
dv d v
a t v t
dt dt

6. 2
0 0
1
( )
2
s t gt v t s
In general, the position function for a falling object is given as
where s0 is initial position, v0 is initial velocity, and g is the
acceleration due to gravity. On earth that is -32 feet per
second per second or -9.8 meters per second per second.

7. Ex 10 p. 114 Using the derivative to find velocity
At time t=0, a diver jumps from a platform diving board
that is 32 feet above the water. The position of the diver is
given by
a. When does the diver hit the water?
b. What is the diver’s velocity on impact?
2
( ) 16 16 32s t t t
a. Solve for s = 0. 2
0 16 16 32t t
Hint: solve(expression, variable, guess, {lower, upper}) or
solver, or polysmlt app! Or quadratic formula!
t = -1 or 2
b. Find s’(2): '( ) 32 16s t t
'(2) 32 2 16 48 /secs ft

8. 35
30
25
20
15
10
5
s x = -16 x2+16 x+32
(0.5, 36)
Notice the diver moves
upward for the first half
second, because the
velocity is positive for the
first half second. When the
velocity is zero, the diver
has reached the maximum
height of the dive.

9. Particle Motion
A particle moves along a line so that its position at any time t 
0 is given by the function s(t) = t2 – 4t + 3, where s is in meters, t
is in seconds.
a) Find the displacement of the particle during the first 2 secs.
Sol: The displacement is given by s(2) – s(0) = (-1) – 3 = -4
b) Find the average velocity of the particle during the first 4 secs
Sol: Avg velocity is (4) (0) 3 3
0 m/sec
4 0 4
s s
c) Find the instantaneous velocity of the particle when t = 4
Sol: Instantaneous velocity if just the velocity v(t) where
v(t) = ds/dt = 2t – 4. So v(4) = 4 m/sec
d) Find the acceleration of the particle when t = 4
Sol: Acceleration a(t) at any time t is a(t) = dv/dt = 2 m/sec2

10. For 0t 2, v(t) < 0, so the particle is moving to
the left. (Notice s(t) is decreasing). The particle
starts (t = 0) at s = 3 and moves left, arriving at the
origin t = 1when s = 0.
It continues moving left until it reaches the point
s = -1 at t = 2.
At t = 2, v = 0, so the particle is at rest.
For t >2, v(t) > 0, so particle is going to right.
(Notice s(t) is increasing).
In this interval, the particle starts at s = -1, moving
to the right through the origin and continuing to
the right for the rest of the time.
The particle changes direction at t = 2 when v = 0.

11. f) Use parametric graphing to view the motion of the particle
on the horizontal line y = 2
Sol: Change mode to PAR (parametric)
Enter
And graph in window [-5, 5] by [-2, 4]
with Tmin = 0, Tmax = 10 (could go to
infinity) and Xscl = Yscl= 1. Use trace
to follow the path of the particle.
If you change your Tstep = 0,5, you see
what is happening every half second.
2
1TX 4 3,T T 1T 2,Y

12. 2.2b Assignment: p. 115 #75-76, 83-
90, 93-96, 103-104 and
Particle Motion Prob 1.