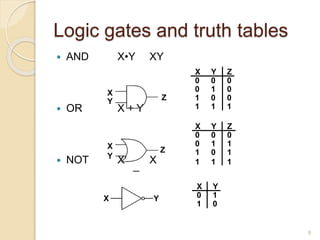
This document provides an introduction to Boolean algebra and its applications in digital logic. It discusses how Boolean algebra was developed by George Boole in the 1800s as an algebra of logic to represent logical statements as either true or false. The document then explains how Boolean algebra is used to perform logical operations in digital computers by representing true as 1 and false as 0. It introduces the basic logical operators of AND, OR, and NOT and provides their truth tables. The rest of the document discusses topics such as logic gates, truth tables, minterms, maxterms, and how to realize Boolean functions using sum of products and product of sums forms.

1. Boolean Algebra
‘An algebra of Logic’

2. Introduction
 Developed by English Mathematician
George Boole in between 1815 -
1864.
 It is described as an algebra of logic or
an algebra of two values i.e True or
False.
 The term logic means a statement
having binary decisions i.e True/Yes or
False/No.

3. Application of Boolean algebra
 It is used to perform the logical operations in
digital computer.
 In digital computer True represent by ‘1’ (high
volt) and False represent by ‘0’ (low volt)
 Logical operations are performed by logical
operators. The fundamental logical operators
are:
1. AND (conjunction)
2. OR (disjunction)
3. NOT (negation/complement)

4. AND operator
 It performs logical multiplication and
denoted by (.) dot.
X Y X.Y
0 0 0
0 1 0
1 0 0
1 1 1

5. OR operator
 It performs logical addition and
denoted by (+) plus.
X Y X+Y
0 0 0
0 1 1
1 0 1
1 1 1

6. NOT operator
 It performs logical negation and
denoted by (-) bar. It operates on
single variable.
X X (means complement of
x)
0 1
1 0

7. Truth Table
 Truth table is a table that contains all
possible values of logical
variables/statements in a Boolean
expression.
No. of possible combination =
2n, where n=number of variables used
in a Boolean expression.

8. Truth Table
 The truth table for XY + Z is as
follows:
Dec X Y Z XY XY+Z
0 0 0 0 0 0
1 0 0 1 0 1
2 0 1 0 0 0
3 0 1 1 0 1
4 1 0 0 0 0
5 1 0 1 0 1
6 1 1 0 1 1
7 1 1 1 1 1

9. Logic gates and truth tables
 AND X•Y XY
 OR X + Y
 NOT X' X
9
X
Y Z
X Y Z
0 0 0
0 1 0
1 0 0
1 1 1
X
Y
Z
X Y
_
X Y Z
0 0 0
0 1 1
1 0 1
1 1 1
X Y
0 1
1 0

10. Logic gates and truth tables
 NAND
 NOR
10
X Y XY X Y Z
0 0 1
0 1 1
1 0 1
1 1 0
X Y Z
0 0 1
0 1 0
1 0 0
1 1 0
X Y
X
Y
Z
Z
X
Y

11. Logic gates and truth tables
 XOR
 XNOR
11
X
Y
Z
Z
X
Y
X Y Z
0 0 0
0 1 1
1 0 1
1 1 0
X Y Z
0 0 1
0 1 0
1 0 0
1 1 1
X Y
X Y

12. Realizing Boolean formulas
 F = (A•B)’ + C•D  F = C•(A+B)’
12
F
A
B
C
D
A
B
C
F

13. Basic Theorem of Boolean Algebra
T1 : Properties of 0
(a) 0 + A = A
(b) 0 A = 0
T2 : Properties of 1
(a) 1 + A = 1
(b) 1 A = A

14. Basic Theorem of Boolean Algebra
T3 : Commutative Law
(a) A + B = B + A
(b) A B = B A
T4 : Associate Law
(a) (A + B) + C = A + (B + C)
(b) (A B) C = A (B C)
T5 : Distributive Law
(a) A (B + C) = A B + A C
(b) A + (B C) = (A + B) (A + C)
(c) A+A’B = A+B

15. Basic Theorem of Boolean Algebra
T6 : Indempotence (Identity ) Law
(a) A + A = A
(b) A A = A
T7 : Absorption (Redundance) Law
(a) A + A B = A
(b) A (A + B) = A

16. Basic Theorem of Boolean Algebra
T8 : Complementary Law
(a) X+X’=1
(b) X.X’=0
T9 : Involution
(a) x’’ = x
T10 : De Morgan's Theorem
(a) (X+Y)’=X’.Y’
(b) (X.Y)’=X’+Y’

19. Realizing truth tables
 Given a truth table
1. Write the Boolean expression
2. Minimize the Boolean expression
3. Draw as gates
19

23. Canonical form of Boolean Expression
(Standard form) Contd..
Convert AB+AC in Canonical SOP
(Standard SOP)
Sol. AB + AC
AB(C+C’) + AC(B+B’)
ABC+ABC’+ABC+AB’C
ABC+ABC’+AB’C
Distributive law

24. Canonical form of Boolean Expression
(Standard form) Contd..
Convert (A+B)(A+C) in Canonical SOP
(Standard SOP)
Sol. (A+B).(A+C)
(A+B)+(C.C’) . (A+C)+(B.B’)
(A+B+C).(A+B+C’).(A+B+C)(A+B’+C)
(A+B+C).(A+B+C’)(A+B’+C)
Distributive law
Remove duplicates

25. Canonical form of Boolean Expression
(Standard form) Contd..
Minterm and Maxterm
Individual term of Canonical Sum of Products (SOP) is
called Minterm. In otherwords minterm is a product of
all the literals (with or without bar) within the Boolean
expression.
Individual term of Canonical Products of Sum (POS) is
called Maxterm. In otherwords maxterm is a sum of all
the literals (with or without bar) within the Boolean
expression.

26. Minterms & Maxterms for 2 variables (Derivation
of Boolean function from Truth Table)
x y Index Minterm Maxterm
0 0 0 m0 = x’ y’ M0 = x + y
0 1 1 m1 = x’ y M1 = x + y’
1 0 2 m2 = x y’ M2 = x’ + y
1 1 3 m3 = x y M3 = x’ + y’
The minterm mi should evaluate to 1 for each
combination of x and y.
The maxterm is the complement of the minterm

27. Minterms & Maxterms for 3 variables
Maxterm Mi is the complement of minterm mi
Mi = mi and mi = Mi
M3 = x + y + zm3 = x y z3110
M4 = x + y + zm4 = x y z4001
M5 = x + y + zm5 = x y z5101
M6 = x + y + zm6 = x y z6011
1
1
0
0
y
1
0
0
0
x
1
0
1
0
z
M7 = x + y + zm7 = x y z7
M2 = x + y + zm2 = x y z2
M1 = x + y + zm1 = x y z1
M0 = x + y + zm0 = x y z0
MaxtermMintermIndex
M3 = x + y + zm3 = x y z3110
M4 = x + y + zm4 = x y z4001
M5 = x + y + zm5 = x y z5101
M6 = x + y + zm6 = x y z6011
1
1
0
0
y
1
0
0
0
x
1
0
1
0
z
M7 = x + y + zm7 = x y z7
M2 = x + y + zm2 = x y z2
M1 = x + y + zm1 = x y z1
M0 = x + y + zm0 = x y z0
MaxtermMintermIndex

28. Solved Problem
Prob. Find the minterm designation of
XY’Z’
Sol. Subsitute 1’s for non barred and
0’s for barred letters
Binary equivalent = 100
Decimal equivalent = 4
Thus XY’Z’=m4

29. Minterms
 Minterms are AND terms with every variable
present in either true or complemented form.
 Given that each binary variable may appear
normal (e.g., x) or complemented (e.g., ), there
are 2n minterms for n variables.
 Example: Two variables (X and Y) produce
2 x 2 = 4 combinations:
(both normal)
(X normal, Y complemented)
(X complemented, Y normal)
(both complemented)
 Thus there are four minterms of two variables.
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
29
YX
XY
YX
YX
x

30. Maxterms
 Maxterms are OR terms with every variable
in true or complemented form.
 Given that each binary variable may appear
normal (e.g., x) or complemented (e.g., x),
there are 2n maxterms for n variables.
 Example: Two variables (X and Y) produce
2 x 2 = 4 combinations:
(both normal)
(x normal, y complemented)
(x complemented, y normal)
(both complemented)
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
30
YX 
YX 
YX 
YX 

31. Minterms & Maxterms for 2 variables
 Two variable minterms and maxterms.
 The minterm mi should evaluate to 1 for each
combination of x and y.
 The maxterm is the complement of the
minterm
x y Index Minterm Maxterm
0 0 0 m0 = x y M0 = x + y
0 1 1 m1 = x y M1 = x + y
1 0 2 m2 = x y M2 = x + y
1 1 3 m3 = x y M3 = x + y

32. Minterms & Maxterms for 3 variables
M3 = x + y + zm3 = x y z3110
M4 = x + y + zm4 = x y z4001
M5 = x + y + zm5 = x y z5101
M6 = x + y + zm6 = x y z6011
1
1
0
0
y
1
0
0
0
x
1
0
1
0
z
M7 = x + y + zm7 = x y z7
M2 = x + y + zm2 = x y z2
M1 = x + y + zm1 = x y z1
M0 = x + y + zm0 = x y z0
MaxtermMintermIndex
Maxterm Mi is the complement of minterm
mi

33. Purpose of the Index
 Minterms and Maxterms are designated with an
index
 The index number corresponds to a binary pattern
 The index for the minterm or maxterm, expressed
as a binary number, is used to determine whether
the variable is shown in the true or complemented
form
 For Minterms:
◦ ‘1’ means the variable is “Not Complemented” and
◦ ‘0’ means the variable is “Complemented”.
 For Maxterms:
◦ ‘0’ means the variable is “Not Complemented” and
◦ ‘1’ means the variable is “Complemented”.
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
33

34. Standard Order
 All variables should be present in a minterm or
maxterm and should be listed in the same order
(usually alphabetically)
 Example: For variables a, b, c:
◦ Maxterms (a + b + c), (a + b + c) are in standard order
◦ However, (b + a + c) is NOT in standard order
(a + c) does NOT contain all variables
◦ Minterms (a b c) and (a b c) are in standard order
◦ However, (b a c) is not in standard order
(a c) does not contain all variables
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
34

35. Sum-Of-Minterm (SOM)
 Sum-Of-Minterm (SOM) canonical form:
Sum of minterms of entries that evaluate to ‘1’
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
35
x y z F Minterm
0 0 0 0
0 0 1 1 m1 = x y z
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 1 m6 = x y z
1 1 1 1 m7 = x y z
F = m1 + m6 + m7 = ∑ (1, 6, 7) = x y z + x y z + x
y z
Focus on
the ‘1’
entries

36. Sum-Of-Minterm Examples
 F(a, b, c, d) = ∑(2, 3, 6, 10, 11)
 F(a, b, c, d) = m2 + m3 + m6 + m10 +
m11
 G(a, b, c, d) = ∑(0, 1, 12, 15)
 G(a, b, c, d) = m0 + m1 + m12 + m15
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
36
+ a b c d
+ a b c da b c d + a b c d+ a b c d + a b c d
+ a b c da b c d+ a b c d

37. Product-Of-Maxterm (POM)
 Product-Of-Maxterm (POM) canonical form:
Product of maxterms of entries that evaluate to
‘0’
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
37
x y z F Maxterm
0 0 0 1
0 0 1 1
0 1 0 0 M2 = (x + y + z)
0 1 1 1
1 0 0 0 M4 = (x + y + z)
1 0 1 1
1 1 0 0 M6 = (x + y + z)
1 1 1 1
Focus on
the ‘0’
entries
F = M2·M4·M6 = ∏ (2, 4, 6) = (x+y+z) (x+y+z)
(x+y+z)

38. Product-Of-Maxterm Examples
 F(a, b, c, d) = ∏(1, 3, 6, 11)
 F(a, b, c, d) = M1 · M3 · M6 · M11
 G(a, b, c, d) = ∏(0, 4, 12, 15)
 G(a, b, c, d) = M0 · M4 · M12 · M15
(a+b+c+d)
(a+b+c+d
)
(a+b+c+d
)
(a+b+c+d
)
(a+b+c+d)
(a+b+c+d
)
(a+b+c+d
)
(a+b+c+d
)

39. Observations
 We can implement any function by "ORing" the
minterms corresponding to the ‘1’ entries in the function
table. A minterm evaluates to ‘1’ for its corresponding
entry.
 We can implement any function by "ANDing" the
maxterms corresponding to ‘0’ entries in the function
table. A maxterm evaluates to ‘0’ for its corresponding
entry.
 The same Boolean function can be expressed in two
canonical ways: Sum-of-Minterms (SOM) and Product-
of-Maxterms (POM).
 If a Boolean function has fewer ‘1’ entries then the
SOM canonical form will contain fewer literals than
POM. However, if it has fewer ‘0’ entries then the POM
form will have fewer literals than SOM.
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
39

40. Converting to Sum-of-Minterms Form
 A function that is not in the Sum-of-Minterms form
can be converted to that form by means of a truth
table
 Consider F = y + x z
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
40
x y z F Minterm
0 0 0 1 m0 = x y z
0 0 1 1 m1 = x y z
0 1 0 1 m2 = x y z
0 1 1 0
1 0 0 1 m4 = x y z
1 0 1 1 m5 = x y z
1 1 0 0
1 1 1 0
F = ∑(0, 1, 2, 4, 5) =
m0 + m1 + m2 + m4 +
m5 =
x y z + x y z + x y z +
x y z + x y z

41. Converting to Product-of-Maxterms Form
 A function that is not in the Product-of-Minterms
form can be converted to that form by means of a
truth table
 Consider again: F = y + x z
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
41
x y z F Minterm
0 0 0 1
0 0 1 1
0 1 0 1
0 1 1 0 M3 = (x+y+z)
1 0 0 1
1 0 1 1
1 1 0 0 M6 = (x+y+z)
1 1 1 0 M7 = (x+y+z)
F = ∏(3, 6, 7) =
M3 · M6 · M7 =
(x+y+z) (x+y+z) (x+y+z)

42. Conversions Between Canonical Forms
F = m1+m2+m3+m5+m7 = ∑(1, 2, 3, 5, 7) =
x y z + x y z + x y z + x y z + x y z
F = M0 · M4 · M6 = ∏(0, 4, 6) =
(x+y+z)(x+y+z)(x+y+z)
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
42
x y z F Minterm Maxterm
0 0 0 0 M0 = (x + y + z)
0 0 1 1 m1 = x y z
0 1 0 1 m2 = x y z
0 1 1 1 m3 = x y z
1 0 0 0 M4 = (x + y + z)
1 0 1 1 m5 = x y z
1 1 0 0 M6 = (x + y + z)
1 1 1 1 m7 = x y z

43. Algebraic Conversion to Sum-of-Minterms
 Expand all terms first to explicitly list all
minterms
 AND any term missing a variable v with (v + v)
 Example 1: f = x + x y (2 variables)
f = x (y + y) + x y
f = x y + x y + x y
f = m3 + m2 + m0 = ∑(0, 2, 3)
 Example 2: g = a + b c (3 variables)
g = a (b + b)(c + c) + (a + a) b c
g = a b c + a b c + a b c + a b c + a b c + a b c
g = a b c + a b c + a b c + a b c + a b c
g = m1 + m4 + m5 + m6 + m7 = ∑ (1, 4, 5, 6, 7)
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
43

44. Algebraic Conversion to Product-of-Maxterms
 Expand all terms first to explicitly list all
maxterms
 OR any term missing a variable v with v · v
 Example 1: f = x + x y (2
variables)
Apply 2nd distributive law:
f = (x + x) (x + y) = 1 · (x + y) = (x + y) = M1
 Example 2: g = a c + b c + a b (3 variables)
g = (a c + b c + a) (a c + b c + b)(distributive)
g = (c + b c + a) (a c + c + b) (x + x y =
x + y)
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
44

45. Function Complements
 The complement of a function expressed
as a sum of minterms is constructed by
selecting the minterms missing in the
sum-of-minterms canonical form
 Alternatively, the complement of a
function expressed by a Sum of Minterms
form is simply the Product of Maxterms
with the same indices
 Example: Given F(x, y, z) = ∑ (1, 3, 5, 7)
F(x, y, z) = ∑ (0, 2, 4, 6)
F(x, y, z) = ∏ (1, 3, 5, 7)
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
45

46. Summary of Minterms and Maxterms
 There are 2n minterms and maxterms for Boolean
functions with n variables.
 Minterms and maxterms are indexed from 0 to 2n
– 1
 Any Boolean function can be expressed as a
logical sum of minterms and as a logical product
of maxterms
 The complement of a function contains those
minterms not included in the original function
 The complement of a sum-of-minterms is a
product-of-maxterms with the same indices
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
46

47. Standard Forms
 Standard Sum-of-Products (SOP) form:
equations are written as an OR of AND
terms
 Standard Product-of-Sums (POS) form:
equations are written as an AND of OR
terms
 Examples:
◦ SOP:
◦ POS:
 These “mixed” forms are neither SOP nor
POS
◦
◦
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
47
BCBACBA 
C·)CB(A·B)(A 
C)(AC)B(A 
B)(ACACBA 

48. Standard Sum-of-Products (SOP)
 A sum of minterms form for n variables
can be written down directly from a
truth table.
◦ Implementation of this form is a two-level
network of gates such that:
◦ The first level consists of n-input AND gates
◦ The second level is a single OR gate
 This form often can be simplified so
that the corresponding circuit is
simpler.
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
48

49. Standard Sum-of-Products (SOP)
 A Simplification Example:
 Writing the minterm expression:
F = A B C + A B C + A B C + ABC + ABC
 Simplifying:
F = A B C + A (B C + B C + B C + B C)
F = A B C + A (B (C + C) + B (C + C))
F = A B C + A (B + B)
F = A B C + A
F = B C + A
 Simplified F contains 3 literals compared to
15
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
49
)7,6,5,4,1()C,B,A(F S=

50. AND/OR Two-Level Implementation
 The two implementations for F are shown
below
F
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
F
B
C
A

51. SOP and POS Observations
 The previous examples show that:
◦ Canonical Forms (Sum-of-minterms, Product-of-
Maxterms), or other standard forms (SOP, POS) differ in
complexity
◦ Boolean algebra can be used to manipulate equations
into simpler forms
◦ Simpler equations lead to simpler implementations
 Questions:
◦ How can we attain a “simplest” expression?
◦ Is there only one minimum cost circuit?
◦ The next part will deal with these issues
Boo
lea
n
Alg
ebr
a
and
Log
ic
Gat
es
51