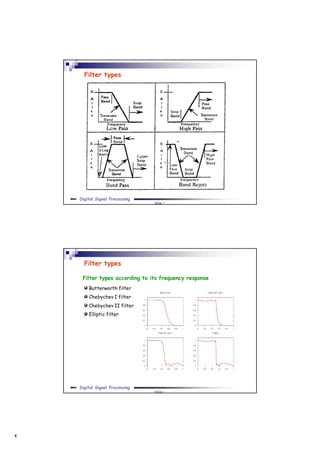
Filters can be classified based on the range of frequencies they allow to pass. Butterworth filters provide maximally flat frequency response in the passband. They are designed by determining the filter order based on the required stopband attenuation. The poles are then calculated and the transfer function is the ratio of polynomials formed from the poles. Butterworth filter design involves converting specifications to a lowpass prototype, finding the poles, and transforming the prototype to the desired filter type.