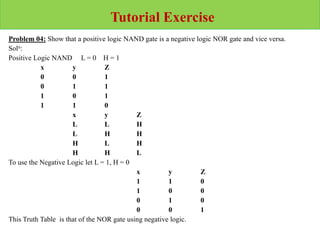
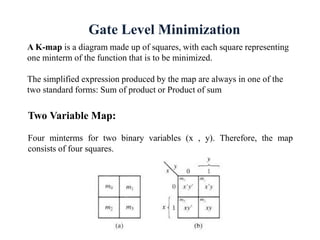
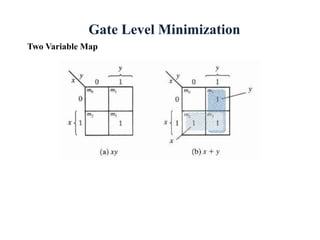
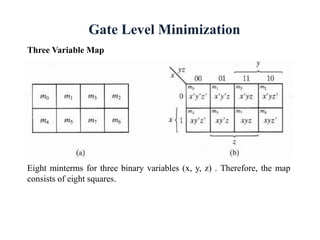
This document discusses digital system design and Boolean algebra concepts. It covers canonical and standard forms, minterms and maxterms, conversions between forms, sum of minterms, product of maxterms, and other logic operations. Examples are provided to demonstrate minimizing Boolean functions using K-maps and converting between standard forms. DeMorgan's laws and other Boolean algebra properties are also explained. Tutorial problems are given at the end to practice simplifying Boolean expressions and converting between standard forms.

1. Course Code: CSE-411
Course Name: Digital System Design
Credit: 3.0
Md Jubayer Faisal
Lecturer, Dept. Of EEE, City University
Canonical and Standard Forms

2. Contents
 Canonical and Standard Forms
 Minterms and Maxterms
 Conversion between Canonical Forms
 Sum of minterms
 Product of maxterms
 Standard Form
 Other Logic Operations
 Tutorial Solve
Page 2

3. Canonical and Standard Forms
Page 3
An n-variable maxterm is a normal sum term
with n literals. There are 2n such sum terms
which can be written as M i
An n-variable minterm is a normal product term
with n literals. There are 2n such product terms
which can be written as m i .
Minterms and Maxterms

4. Gate Level Minimization
A K-map is a diagram made up of squares, with each square representing
one minterm of the function that is to be minimized.
The simplified expression produced by the map are always in one of the
two standard forms: Sum of product or Product of sum
Two Variable Map:
Four minterms for two binary variables (x , y). Therefore, the map
consists of four squares.

5. Gate Level Minimization
Two Variable Map

6. Gate Level Minimization
Three Variable Map
Eight minterms for three binary variables (x, y, z) . Therefore, the map
consists of eight squares.

7. Gate Level Minimization
Example 1: Simplify the Boolean function F(x, y, z) = 𝜮 (2.3.4.5)
F = x'y + xy’
Solution:

8. Gate Level Minimization
Example 1: Simplify the Boolean function F(x, y, z) = 𝜮 (3,4,6,7)
Solution:
F = yz + xz'

9. Canonical and Standard Forms
Page 9
An n-variable maxterm is a normal sum term
with n literals. There are 2n such sum terms
which can be written as M i
An n-variable minterm is a normal product term
with n literals. There are 2n such product terms
which can be written as m i .
Minterms and Maxterms
i denotes the decimal equivalent
of the binary number of the
miniterm designated.
Also called standard sum

10. Canonical and Standard Forms
Page 10
Example: There are 23（8）minterms in a 3-variable
expression
C
B
A C
B
A
m0 m1
000 001
0 1
Minterms
Binary
code
Decimal
number
mi
C
B
A BC
A C
B
A C
B
A C
AB ABC
m2 m3 m4 m5 m6 m7
010 011 100 101 110 111
2 3 4 5 6 7

11. Canonical and Standard Forms
 Minterms and Maxterms for a 3-Variable logic function
Page 11

12. Canonical and Standard Forms
Dept. of ECE, Khulna University of Engineering & Technology (KUET), Bangladesh Page 12
 Example: from the following truth table, determine
the sum of minterms expression.
x y z Function f1 Function f2
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
0
1
0
0
1
0
0
1
0
0
0
1
0
1
1
1
f1=x'y'z+ xy'z'+xyz
=m1+m4 +m7
f2=x'yz+ xy'z+xyz' +xyz
=m3+m5+m6 +m7
f1=(x+y+z) (x+y'+z) (x+y'+z')
(x'+y+z') (x'+y'+z)
=M0 M2 M3 M5 M6
f2= (x+y+z) (x+y+z')
(x+y'+z) (x'+y+z)
=M0 M1 M2 M4

13. Canonical and Standard Forms
Page 13
 Sum of minterms
Step2: repeat step1 until all resulting product terms contain all
variables in the domain to standard form, the number of product
terms is doubled for each missing variable.
Step1: multiply each nonstandard product term by a term made up
of the sum of a missing variable and its complement. This results
in two product terms. As you know, you can multiply anything by
1 without changing its value.
The procedure of converting the Boolean function into Sum of
minterms

14. Canonical and Standard Forms
Dept. of ECE, Khulna University of Engineering & Technology (KUET), Bangladesh Page 14
 Sum of minterms
A=A(B+B')=AB+AB'=AB(C+C') + AB'(C+C')
=ABC+ABC' + AB'C+ AB' C'
Example: express the Boolean function F=A+B'C in sum of
minterms.
B'C= B'C(A+A')= AB'C+ A'B'C
F=A+B'C = ABC + ABC' + AB'C + AB'C' + A'B'C
=m1 + m4 + m5 + m6 + m7
In short, F(A, B, C) =(1,4,5,6,7)

15. Canonical and Standard Forms
Page 15
 Product of maxterms
Step2: any missing variable x in each OR term is Ored with xx'.
Then repeat step1 until all resulting sum terms contain all
variables in the domain to standard form, the number of sum terms
is doubled for each missing variable.
Step1: bring the Boolean function into a form of OR terms. This
may be done by using the distributive law, x+yz=(x+y)(x+z).
The procedure of converting the Boolean function into
product of maxterms form

16. Canonical and Standard Forms
Page 16
 Product of maxterms
F= xy + x'z = ( xy + x' ) ( xy + z )
= ( x + x' ) ( y + x' ) ( x + z ) ( y + z )
= ( x' + y ) ( x + z ) ( y + z )
Example: express the Boolean function F= xy+x'z in product
of maxterms.
( x' + y ) = x' + y + zz' = ( x' + y + z ) ( x' + y + z' )
( x + z ) = x + z + yy' = ( x + z + y ) ( x + z + y' )
( y + z ) = y + z + xx' = ( y + z + x ) ( y + z + x' )
F= ( x + y + z ) ( x + y' + z ) ( x' + y + z ) ( x' + y + z' )
=M0 M2 M4 M5= ∏ (0,2,4,5)
distributive law
x+yz=(x+y)(x+z)

17. Canonical and Standard Forms
Page 17
 Conversion between Canonical Forms
• Based on the correspondance Between the truth
table and canonical form, we can easily create an
algebraic representation of a logic function from
its truth table.
• Boolean function expressed as a sum of minterms
or product of maxterms

18. Canonical and Standard Forms
Dept. of ECE, Khulna University of Engineering & Technology (KUET), Bangladesh Page 18
Standard Sum-of-Product (minimum term) Expression
F(A、B、C、D) D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
A 



8
5
1
0 m
m
m
m 




 )
8
5
1
0
(
m 、
、
、
Example： F(A、B、C、D) C
B
A
B
A 


F(A、B、C、D) C
B
A
B
A 

 C
B
A
B
A 
 
C
B
A
)
C
C
(
B
A 


1
2
3 m
m
m 

 
 )
3
2
1
(
m 、
、

19. Canonical and Standard Forms
Page 19
 Five Expressions
F(A、B、C) C
A
AB
 “AND―OR or Sum-of-Product”
)
B
A
)(
C
A
( 

 “OR―AND”
C
A
AB
 “NAND―NAND”
B
A
C
A 


 “NOR―NOR”
B
A
C
A 
 
 “AND―OR―NOT”
 Conversions between Different Expressions
C
A
AB
F 
 C
A
AB 
 C
A
AB


20. Logic Operations
Dept. of ECE, Khulna University of Engineering & Technology (KUET), Bangladesh Page 20
 Other Logic Operations
x y F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 F13 F14 F15
0 0
0 1
1 0
1 1
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
• There are 22n functions for n binary function.
• For two variables, the number of possible Boolean functions
is 16.
• Truth Table for the 16 Functions of Two Binary Variables.

21. Logic Operations
Page 21
Boolean
function
Operator
symbol
Name comments
F0 = 0
F1 = xy
F2 = xy'
F3 = x
F4 = x'y
F5 = y
F6=xy'+x'y
F7=x+y
x • y
x / y
y / x
x  y
x+y
Null
AND
Inhibition
Transfer
Inhibition
Transfer
Exclusive-OR
OR
Binary constant 0
x and y
x, but not y
x
y, but not x
y
x or y, but not both
x or y

22. Logic Operations
Dept. of ECE, Khulna University of Engineering & Technology (KUET), Bangladesh Page 22
Boolean
function
Operator
symbol
Name comments
F8 =(x+y)'
F9=xy+x'y'
F10 = y'
F11 = x+y'
F12 = x'
F13 = x'+y
F14 =(xy)'
F15 = 1
x y
(x  y)'
y'
x y
x'
x y
x y
NOR
Equivalence
complement
Implication
complement
Implication
NAND
Identity
Not-OR
x equals y
Not y
If y, then x
Not x
If x, then y
Not-AND
Binary constant 1
U
U

23. Logic Operations
Page 23
XOR Operation
XNOR Operation
Logic Symbol
Logic Symbol
A B F
0 0
0 1
1 0
1 1
0
1
1
0
A B F
0 0
0 1
1 0
1 1
1
0
0
1
Logic Expression:
F=AB = AB+AB
Logic Expression:
F=A⊙B = AB

24. Tutorial Solve
DeMorgan's Law
Graphical representation of DeMorgan's Law
x
y
x
y
x
y
(X.Y)' X' + Y'
x
y
x
y
x
y
(X+Y)' X'.Y'

25. Tutorial Solve
Problem 01: Reduce the following Boolean expressions to the indicated number of
literals:
(a) A’C’ + ABC + AC’ to three literals
(b) (x’y’+z)’ + z + xy + wz to three literals
(c) A’B(D’+C’D) + B(A+A’CD) to one literal
(d) (A’+C)(A’+C’)(A+B+C’D) to four literals
Soln: a)
A’C’ + ABC + AC’ = A’C’ + AC’ + ABC
= C’(A’+ A) + ABC
= C’∙1 + ABC
= C’ + ABC
= (C’+ AB)(C’+C) [distributive]
= AB + C’

26. Tutorial Solve
Soln: b) (x’y’+z)’ + z + xy + wz = (x’y’+z)’ + z + wz + xy
= (x’y’+z)’ + z(1+ w) + xy
= (x’y’+z)’ + z + xy
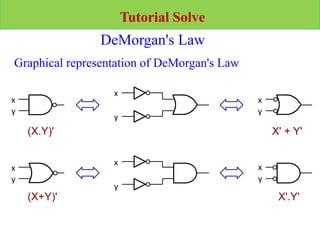
= (x + y)z’ + z + xy [DeMorgan]
= (z + (x + y)) ∙ (z + z’) + xy [distributive]
= (z + (x + y)) ∙ 1 + xy
= x + y + z + xy
= x + y + z [absorption]
Soln: c) A’B(D’ + C’D) + B(A+A’CD) = A’BD’ + A’BC’D + AB+ A’BCD
= A’BD(C+C’)+ A’BD’+ AB
= A’BD+ A’BD’+ AB
= A’B(D+D’)+ AB
= A’B+ AB
= B(A’+ A) = B

27. Tutorial Solve
Soln: d) (A’+C)(A’+C’)(A+B+C’D) = (A’+C)(A’+C’)(A+B+C’D)
= (A’ + CC’)(A + B + C’D)
= A’(A + B + C’D)
= A’A + A’B + A’C’D
= A’B + A’C’D
= A’(B + C’D)

28. Tutorial Solve
Problem 02: Convert the following to the other canonical form:
(a) F (x, y , z) = ∑ (1,3,7) (b) F(A,B,C,D)= ∏ (0,1,2,3,4,6,12)
Soln: a) F (x, y, z) = ∑ (1,3,7) = ∏ (0,2,4,5,6)
F (x, y, z) =
Soln: b) F (A,B,C,D) = ∏ (0,1,2,3,4,6,12) = ∑ (5,7,8,9,10,11,13,14,15)
F(A,B,C,D) =
)
(
)
(
)
(
)
(
)
( z
y
x
z
y
x
z
y
x
z
y
x
z
y
x 













)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
( ABCD
D
ABC
D
C
AB
CD
B
A
D
C
B
A
D
C
B
A
D
C
B
A
BCD
A
D
C
B
A 








29. Tutorial Exercise
Problem 03: Show that the dual of the exclusive-OR is equal to its complement.
Soln:
XOR
X Y = XY’ + X’Y
= (X +Y’) (X’+Y)
= XX’ +XY +X’Y’ +YY’
= XY + X’Y’
= (X Y)’ = XNOR

30. Tutorial Exercise
Problem 04: Show that a positive logic NAND gate is a negative logic NOR gate and vice versa.
Soln:
Positive Logic NAND L = 0 H = 1
x y Z
0 0 1
0 1 1
1 0 1
1 1 0
x y Z
L L H
L H H
H L H
H H L
To use the Negative Logic let L = 1, H = 0
x y Z
1 1 0
1 0 0
0 1 0
0 0 1
This Truth Table is that of the NOR gate using negative logic.

31. Tutorial Exercise
Problem 05: Show that the dual of the exclusive-OR is equal to its complement.
Soln:
A Ex-OR B = A'B + AB'
Dual of a function: Change the OR to AND and OR to AND operation.
dual = (A'+B)(A+B')
compliment = (A'B+AB')‘
= (A'B)'(AB')'
= (A+B')(A'+B)
which shows compliment and dual of EX-OR are equal.