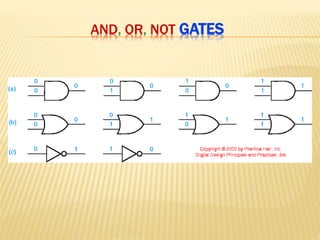
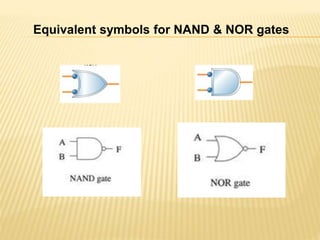
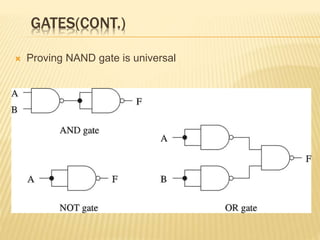
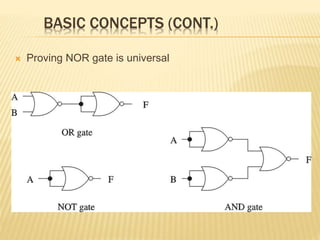
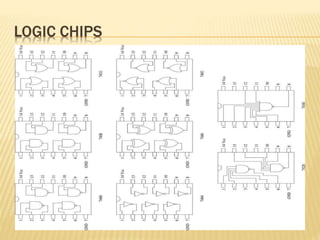
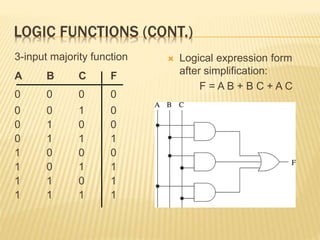
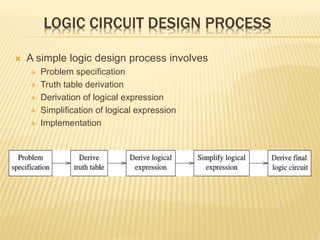
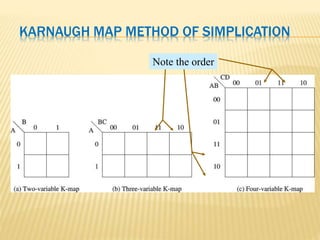
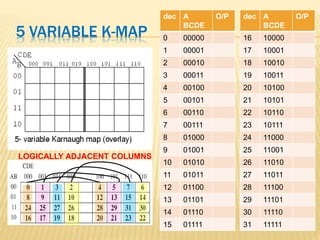
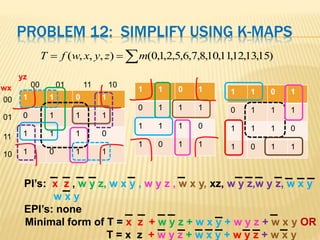
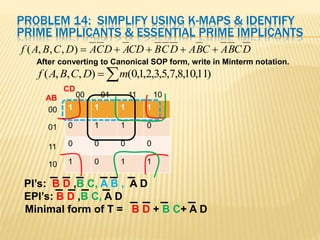
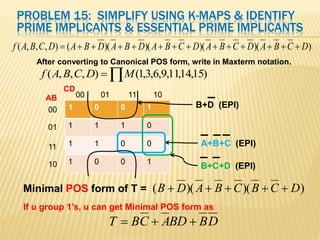
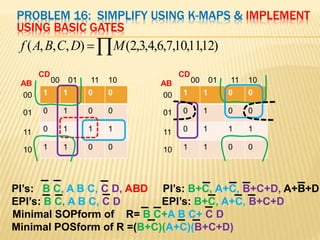
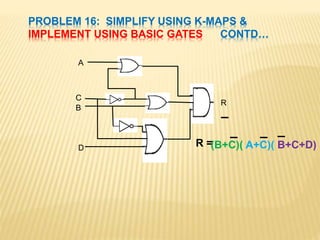
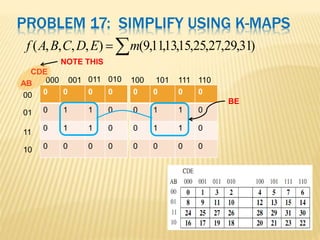
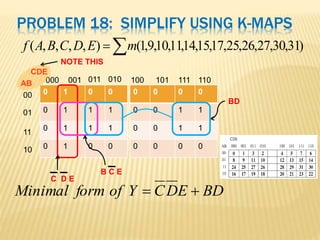
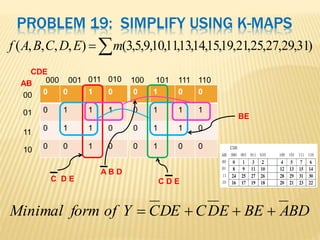
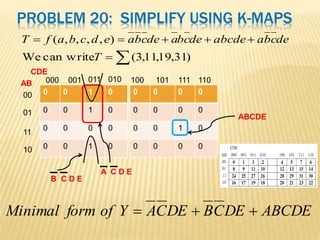
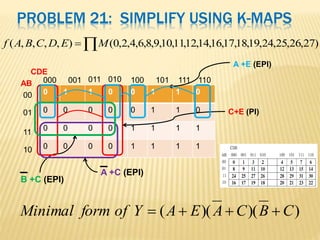
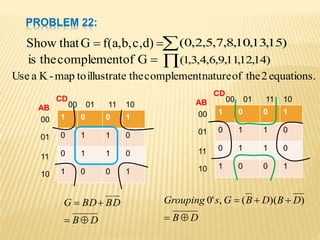
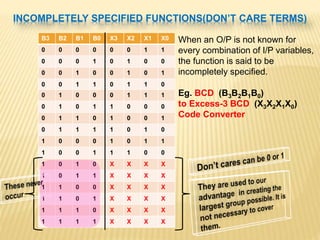
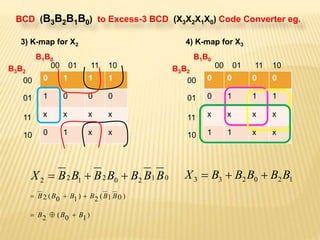
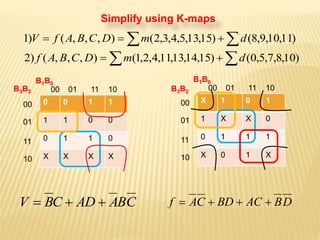
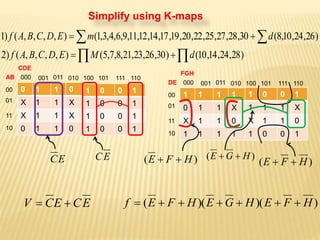
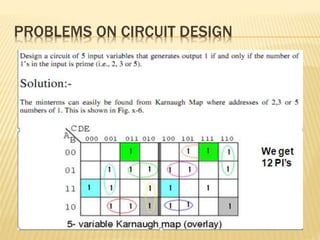
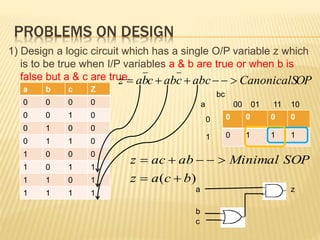
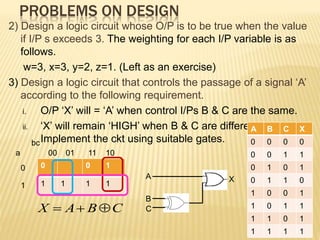
The document covers the principles of combinational logic in digital electronics, describing how basic gates like AND, OR, and NOT are used to create circuits without memory elements. It explains important concepts such as truth tables, Boolean algebra, and canonical forms (SOP and POS), along with methods for logical expression simplification including Karnaugh maps and algebraic manipulation. Additionally, it details the evolution of logic chips from small to very large scale integration (SSI to VLSI) and defines key terms like minterms and maxterms.

1. LOGIC DESIGN
PART A
Unit 1:
PRINCIPLES OF COMBINATIONAL LOGIC-1
Definition of Combinational logic:
It deals with the techniques of combining
basic gates into circuits that perform
some desired function.

2.  Outputs are functions of (present)
inputs.
 No memory element. (like flipflops)
 Do not have feedback from output
to input.
 Egs. Adder, subtractor, decoder,
encoder, multiplexer.
COMBINATIONAL LOGIC

3. BASICS OF DIGITAL ELECTRONICS
 Digital Electronics represents information (0, 1) with only
two discrete values.
 Ideally
“no voltage” (e.g., 0v) represents a 0 and
“full source voltage” (e.g., 5v) represents a 1
 Realistically
“low voltage” (e.g., <1v) represents a 0 and
“high voltage” (e.g., >4v) represents a 1
 We achieve these discrete values by using switches.
 We use transistor switches, which operates at high speed,
electronically, and small in size.

4. GATES
 The most basic digital devices are called
gates.
 Gates got their name from their function
of allowing or blocking (gating) the flow of
digital information.
 A gate has one or more inputs and
produces an output depending on the
input(s).
 A gate is called a combinational circuit.
 Three most important gates are: AND, OR,

5. GATES
 Simple gates
 AND
 OR
 NOT
 Functionality can be
expressed by a truth table
 A truth table lists output for
each possible input
combination
 Precedence
 NOT > AND > OR
 F = A B + A B
= (A (B)) + ((A) B)

6. AND, OR, NOT GATES

7. GATES
 Additional useful gates
 NAND
 NOR
 XOR
 NAND = AND + NOT
 NOR = OR + NOT
 XOR implements
exclusive-OR function
 NAND and NOR gates
require only 2 transistors
 AND and OR need 3
transistors!

8. Equivalent symbols for NAND & NOR gates

9. GATES(CONT.)
 Proving NAND gate is universal

10. BASIC CONCEPTS (CONT.)
 Proving NOR gate is universal

11. LOGIC CHIPS

12. LOGIC CHIPS (CONT.)
 Integration levels
 SSI (small scale integration)
 Introduced in late 1960s
 1-10 gates (previous examples)
 MSI (medium scale integration)
 Introduced in late 1960s
 10-100 gates
 LSI (large scale integration)
 Introduced in early 1970s
 100-10,000 gates
 VLSI (very large scale integration)
 Introduced in late 1970s
 More than 10,000 gates

13. BOOLEAN ALGEBRA

14. BOOLEAN ALGEBRA

15. LOGIC FUNCTIONS
 Logical functions can be expressed in
several ways:
 Truth table
 Logical expressions
 Graphical form
 Example:
 Majority function
 Output is one whenever majority of inputs is 1
 We use 3-input majority function

16. LOGIC FUNCTIONS (CONT.)
3-input majority function
A B C F
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
 Logical expression form
after simplification:
F = A B + B C + A C

17. LOGIC CIRCUIT DESIGN PROCESS
 A simple logic design process involves
 Problem specification
 Truth table derivation
 Derivation of logical expression
 Simplification of logical expression
 Implementation

18. DERIVING LOGICAL EXPRESSIONS
 Derivation of logical expressions from truth
tables
 Sum-of-products (SOP) form
 Product-of-sums (POS) form
 SOP form
 Write an AND term for each input combination that
produces a 1 output
 Write the variable if its value is 1; complement otherwise
 OR the AND terms to get the final expression
 POS form
 Dual of the SOP form

19. SUM OF PRODUCT (SOP) FORM
 3-input majority
function
A B C F
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
SOP logical expression
F = A B C + A B C +
A B C + A B C
 Four product terms
 Because there are 4
rows with a 1 output




20. PRODUCT OF SUM (POS) FORM
 3-input majority function
A B C F
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1




POS logical expression
F = (A + B + C) (A + B + C)
(A + B + C) (A + B + C)
• Four sum terms
Because there are 4 rows with
a 0 output

21. DEFINITIONS:
1) Literal:
It is a Boolean variable or its complement.
Eg. A, B ,C, B
2) Product term:
It is a logical AND of literals or is a literal.
Eg. A B C , B C , AB
3) Sum term:
It is a logical OR of literals or is a literal.
Eg. (A + B + C), (A + B )
4) SOP:
It is the logical OR of multiple product terms.
5) POS:
It is the logical AND of multiple Sum terms.

22. Definitions: 6) Minterm
A minterm is a special case product term which
contains all the input variables (each literal occuring
only once) of the function.
• A function with n variables has 2n minterms
• A three-variable function, such as f(x,y,z), has
23 = 8 minterms.
Minterm Is true when… Shorthand
x’y’z’
x’y’z
x’yz’
x’yz
xy’z’
xy’z
xyz’
xyz
x=0, y=0, z=0
x=0, y=0, z=1
x=0, y=1, z=0
x=0, y=1, z=1
x=1, y=0, z=0
x=1, y=0, z=1
x=1, y=1, z=0
x=1, y=1, z=1
m0
m1
m2
m3
m4
m5
m6
m7

23. DEFINITIONS: 7) MAXTERM
It is a special case Sum term which contains all the
input variables of the function, occurring only once.
 A function with n variables has 2n minterms
 A three-variable function, such as f(x,y,z), has
23 = 8 minterms.
Maxterm Is false when… Shorthand
x + y + z x=0, y=0, z=0 M0
x + y + z’ x=0, y=0, z=1 M1
x + y’ + z x=0, y=1, z=0 M2
x + y’ + z’ x=0, y=1, z=1 M3
x’ + y + z x=1, y=0, z=0 M4
x’ + y + z’ x=1, y=0, z=1 M5
x’ + y’ + z x=1, y=1, z=0 M6
x’ + y’ + z’ x=1, y=1, z=1 M7

25. DEFINITIONS:
8) Canonical SOP
• It is a complete set of minterms that defines when an
O/P variable is a logical 1.
• Canonical or Standard SOP form is an SOP form of
expression in which each product term contains all the
literals.
Eg. A B C + A B C + A B C + A B C
9) Canonical POS
It is a POS form in which each Sum term contains all the
literals.
Eg. (A + B + C) (A + B + C)(A + B + C)

26. CANONICAL SOP FORM & MINTERM NOTATION
Every function can be written as a unique sum of
minterms. You can obtain the canonical SOP form by
picking the rows having O/P =1.



)6,3,2,1,0(
63210
m
mmmmm
CABBCACBACBACBAf

27. CANONICAL POS FORM & MAXTERM
NOTATION

28. CONVERSION

29. Express the following SOP equation in
1) Minterm notation 2) Maxterm notation
abccbabcacbacbaW ),,(
-- Minterm notation







)6,5,2,0(
)7,4,3,1(...
...
...
)2
7431
7431
74317431
7431
MW
MMMMMW
MMMMW
mmmmmmmmW
mmmmW
-- Maxterm notation
 ).7,4,3,1()1 mW

30. Express the following SOP equation in
1) Minterm notation 2) Maxterm notation










)6,4,1(
)7,5,3,2,0(....
)(....
....
)2
)7,5,3,2,0()1
75320
75320
7532075320
75320
MW
MMMMMMX
MmMMMMMX
mmmmmmmmmmX
mmmmmX
mX
abccbabcacbacbaX
ii
… Minterm notation
… Maxterm notation

31. Convert to Canonical SOP form
NMLNMLNLMLMN
NNMLNNMMLLML
LMMNMLR
srqpsrqpspqrsrqpsrqpsqrpqrsp
qqppsrssrrqp
srqpR
m








)())((
)()2
))(())((
)1
)14,10,7,6,5,4,2(

32. Convert to Canonical POS form
))()()((
))((
))(()2
))()((
))()()((
))()()((
))()()((
))((
))(()1
cbacbacbacba
cbaaccba
cbbaX
zyxwzyxwzyxw
zyxwzyxwzyxwzyxw
zyxwzyxwzyxwzyxw
zyxwzyxwzyxwzyxw
zyxxwwzzyyxw
zyxwP










33. LOGICAL EXPRESSION SIMPLIFICATION
Methods:
 Algebraic manipulation
 Use Boolean laws to simplify the expression
 Difficult to use
 Don’t know if you have the simplified form
 Karnaugh map (K-map) method
 Graphical method
 Easy to use
 Can be used to simplify logical expressions with a few
variables.
 Quine Mc-Cluskey method
 Used for more than 6 variable functions
 Tedious procedure

34. 1) ALGEBRAIC MANIPULATION METHOD
 Majority function example
A B C + A B C + A B C + A B C =
A B C + A B C + A B C + A B C + A B C + A
B C
 We can now simplify this expression as
B C + A C + A B
 A difficult method to use for complex
expressions
Added extra

35. KARNAUGH MAP METHOD OF SIMPLICATION
Note the order

36. 5 VARIABLE K-MAP
dec A
BCDE
O/P
0 00000
1 00001
2 00010
3 00011
4 00100
5 00101
6 00110
7 00111
8 01000
9 01001
10 01010
11 01011
12 01100
13 01101
14 01110
15 01111
dec A
BCDE
O/P
16 10000
17 10001
18 10010
19 10011
20 10100
21 10101
22 10110
23 10111
24 11000
25 11001
26 11010
27 11011
28 11100
29 11101
30 11110
31 11111
LOGICALLY ADJACENT COLUMNS

37. DEFINITIONS
 Implicant: Any single minterm(cell) or permitted group
of minterms. Eg.
Implicants are:
 )6,4,2,0(mY
1 0 0 1
1 0 0 1
c
cbcbcaca
cabcbacbacba
,,,,
,,,,
0
1
00 01 11 10
A
BC

38. DEFINITIONS
 Prime Implicant: A group of minterms which
cannot be combined with any other minterms or
groups.
 P.I is c
 P.Is are:
x z, y
1 0 0 1
1 0 0 1
0
1
00 01 11 10
0 1 1 1
0 0 1 1
0
1
00 01 11 10
A
BC
A
BC

39. DEFINITIONS
Essential Prime Implicant:
A prime implicant in which one or more minterms are
unique i.e, it contains atleast one minterm that is not
contained in any other prime implicant.
E.P.Is are:
a c & b c
The simplified exprn. must
contain all EPIs & may or may
not contain non-essential PIs.
The aim is to choose the PI’s so that no cell with ‘1’ is left uncovered.
1 0 1 1
0 0 1 0
0
1
00 01 11 10
Unique ‘1’ cells
A
BC

40. GENERAL RULES FOR USING THE K-
MAP
Combine ones into groups of (1, 2, 4, 8, …)
squares
Form the largest group size.(PIs)
Form the min number of groups.
Two groups should not intersect unless this will
enable a small group to be larger in size.

41.  For every Minterm in the given expression, put a ‘1’
into the corresponding cell & ‘0’ in the other cells.
 Check for logical adjacency for the minterm cells.
( Cells are said to be logically adjacent if there occurs
change in only 1 bit b/w them)
 Eg. Cells 0 & 4 are adjacent 000 100 Arrow shows
changed bit.
 Group logically adjacent 1-cells to form subcubes
such that their size = 2n cells (2,4,8,16..) and it is as
large as possible.
 Then each group represents a product term with
reduced no. of variables.

42. PROBLEM 1: SIMPLIFY USING K-MAPS
 )7,6,3,2,1(),,( zyxfD
0 1 1 1
0 0 1 1
0
1
00 01 11 10
x
yz
PI’s : xz, y
EPI’s: xz, y
Minimal form of D = x z + y

43. PROBLEM 2: SIMPLIFY USING K-MAPS
 )7,5,4,3,2,0(),,( zyxfD
0
1
00 01 11 10
x
yz
1 0 1 1
1 1 1 0
PI’s : y z, x z, x y, x z, x y, yz
EPI’s: none ( because no unique ‘1’ cells)
Minimal form of D = y z + x z + x y OR
D = x z + x y + yz
There are 2 solutions because in each case, all ‘1’ cells
are covered with the chosen set of groups.

44. PROBLEM 3: SIMPLIFY USING K-MAPS
 )15,13,11,9,5,4,1,0(),,,( dcbafK
PI’s : a c, c d, a d
EPI’s: a c, a d
Non-essential PI: c d
Minimal form of K = a c + a d
1 1 0 0
1 1 0 0
0 1 1 0
0 1 1 0
cd
ab 00 01 11 10
00
01
11
10
Unique ‘1’ cells

45. PROBLEM 4: SIMPLIFY USING K-MAPS
 )15,13,10,8,7,5,2,0(),,,( dcbafX
PI’s : b d, b d
EPI’s: b d, b d
Minimal form of X = b d + b d = b d
1 0 0 1
0 1 1 0
0 1 1 0
1 0 0 1
cd
ab 00 01 11 10
00
01
11
10

46. PROBLEM 5: SIMPLIFY USING K-MAPS
 )14,12,11,9,6,4,3,1(),,,( dcbafX
PI’s : b d, b d
EPI’s: b d, b d
Minimal form of X = b d + b d = b d
0 1 1 0
1 0 0 1
1 0 0 1
0 1 1 0
cd
ab 00 01 11 10
00
01
11
10

47. PROBLEM 6: SIMPLIFY USING K-MAPS
 )13,7,6,5,2(),,,( dcbafX
PI’s : a b d, b c d, a c d, a b c
EPI’s: a b d, a b c
Minimal form of X = a b d + a b c + a c d OR
X= a b d + a b c + b c d
0 0 0 1
0 1 1 1
0 1 0 0
0 0 0 0
cd
ab 00 01 11 10
00
01
11
10
Unique ‘1’ cells

48. PROBLEM 7: SIMPLIFY USING K-MAPS
 )14,13,12,9,8,6,5,4,2,1,0(),,,( dcbafX
PI’s : c , a d, b d
EPI’s: c , a d, b d
Minimal form of X = c + a d + b d
1 1 0 1
1 1 0 1
1 1 0 1
1 1 0 0
cd
ab 00 01 11 10
00
01
11
10
Unique ‘1’ cells

49. PROBLEM 8: SIMPLIFY USING K-MAPS
PI’s : cd , a b c, a b c, b d, a d
EPI’s: cd , a b c, a b c
Minimal form of X = cd + a b c + a b c + b d OR
X= cd + a b c + a b c + a d
0 1 1 0
1 1 1 0
0 0 1 0
1 1 1 0
cd
ab 00 01 11 10
00
01
11
10
Unique ‘1’ cells

50. PROBLEM 9: SIMPLIFY USING K-MAPS
 )15,13,11,10,9,8,7,5,1(),,,( dcbafX
0 1 0 0
0 1 1 0
0 1 1 0
1 1 1 1
cd
ab 00 01 11 10
00
01
11
10
Unique ‘1’ cells
PI’s : cd , a d, a b , b d
EPI’s: cd , b d, a b
Minimal form of X = cd + b d + a b

51. PROBLEM 10: SIMPLIFY USING K-MAPS
).......(),,,( OPformcanonicalStoconvertzxyzwxywzyxwfT 
 )14,12,10,8,7,6(mT
0 0 0 0
0 0 1 1
1 0 0 1
1 0 0 1
wx 00 01 11 10
00
01
11
10
Unique ‘1’ cells
yz
PI’s : x y z, w z , w x y.
EPI’s: w z , w x y.
Minimal form of T = w z + w x y.

52. PROBLEM 11: SIMPLIFY USING K-MAPS
 )14,13,12,11,9,6,5,4,3,1(),,,( mzyxwfT
0 1 1 0
1 1 0 1
1 1 0 1
0 1 1 0
wx 00 01 11 10
00
01
11
10
Unique ‘1’ cells
yz
PI’s : y z, x z , x y, x z
EPI’s: x z , x z
Minimal form of T = x z + x z + y z OR
T = x z + x z + x y

53. PROBLEM 12: SIMPLIFY USING K-MAPS
 )15,13,12,11,10,8,7,6,5,2,1,0(),,,( mzyxwfT
1 1 0 1
0 1 1 1
1 1 1 0
1 0 1 1
wx 00 01 11 10
00
01
11
10
yz
PI’s: x z , w y z, w x y , w y z , w x y, xz, w y z,w y z, w x y
w x y
EPI’s: none
Minimal form of T = x z + w y z + w x y + w y z + w x y OR
T = x z + w y z + w x y + w y z + w x y
1 1 0 1
0 1 1 1
1 1 1 0
1 0 1 1
1 1 0 1
0 1 1 1
1 1 1 0
1 0 1 1

54. PROBLEM 13: SIMPLIFY USING K-MAPS. WRITE THE
SIMPLIFIED SOP & POS EXPRESSIONS.
 )15,13,12,11,9,8,7,5,4,0(),,,( Mzyxwf
0 1 1 1
0 0 0 1
0 0 0 1
0 0 0 1
wx 00 01 11 10
00
01
11
10
yz
PI’s: w x y , w x z, y z
EPI’s: w x z , y z
0 1 1 1
0 0 0 1
0 0 0 1
0 0 0 1
wx 00 01 11 10
00
01
11
10
yz
Minimal SOP form of T = w x z + y z
PI’s: w +z , x +z,y+z,w+y,x+y
EPI’s: w +z , x +z, y+z
Minimal POS form of T =(w +z ).(x +z ).(y+z)

55. PROBLEM 14: SIMPLIFY USING K-MAPS & IDENTIFY
PRIME IMPLICANTS & ESSENTIAL PRIME IMPLICANTS
DCBACBADCBCDADCADCBAf ),,,(
1 1 1 1
0 1 1 0
0 0 0 0
1 0 1 1
AB 00 01 11 10
00
01
11
10
CD
PI’s: B D ,B C, A B , A D
EPI’s: B D ,B C, A D
Minimal form of T = B D + B C+ A D
After converting to Canonical SOP form, write in Minterm notation.
 )11,10,8,7,5,3,2,1,0(),,,( mDCBAf

56. PROBLEM 15: SIMPLIFY USING K-MAPS & IDENTIFY
PRIME IMPLICANTS & ESSENTIAL PRIME IMPLICANTS
))()()()((),,,( DCBADCBADCBADBADBADCBAf 
1 0 0 1
1 1 1 0
1 1 0 0
1 0 0 1
AB 00 01 11 10
00
01
11
10
CD
Minimal POS form of T =
After converting to Canonical POS form, write in Maxterm notation.
 )15,14,11,9,6,3,1(),,,( MDCBAf
B+D (EPI)
A+B+C (EPI)
B+C+D (EPI)
))()(( DCBCBADB 
DBBDACBT 
If u group 1’s, u can get Minimal POS form as

57. PROBLEM 16: SIMPLIFY USING K-MAPS & IMPLEMENT
USING BASIC GATES
 )12,11,10,7,6,4,3,2(),,,( MDCBAf
1 1 0 0
0 1 0 0
0 1 1 1
1 1 0 0
AB 00 01 11 10
00
01
11
10
CD
PI’s: B C, A B C, C D, ABD PI’s: B+C, A+C, B+C+D, A+B+D
EPI’s: B C, A B C, C D EPI’s: B+C, A+C, B+C+D
Minimal SOPform of R= B C+A B C+ C D
Minimal POSform of R =(B+C)(A+C)(B+C+D)
1 1 0 0
0 1 0 0
0 1 1 1
1 1 0 0
AB 00 01 11 10
00
01
11
10
CD

58. A
B
C
R
D
PROBLEM 16: SIMPLIFY USING K-MAPS &
IMPLEMENT USING BASIC GATES CONTD…
R =(B+C)( A+C)( B+C+D)

59.  )31,29,27,25,15,13,11,9(),,,,( mEDCBAf
PROBLEM 17: SIMPLIFY USING K-MAPS
0 0 0 0
0 1 1 0
0 1 1 0
0 0 0 0
0 0 0 0
0 1 1 0
0 1 1 0
0 0 0 0
AB 000 001 011
00
01
11
10
CDE
110111101100010
NOTE THIS
BE

60. PROBLEM 18: SIMPLIFY USING K-MAPS
 )31,30,27,26,25,17,15,14,11,10,9,1(),,,,( mEDCBAf
0 1 0 0
0 1 1 1
0 1 1 1
0 1 0 0
0 0 0 0
0 0 1 1
0 0 1 1
0 0 0 0
AB 000 001 011
00
01
11
10
CDE
110111101100010
NOTE THIS
BD
C D E
B C E
BDEDCYofformMinimal 

61. PROBLEM 19: SIMPLIFY USING K-MAPS
 )31,29,27,25,21,19,15,14,13,11,10,9,5,3(),,,,( mEDCBAf
0 0 1 0
0 1 1 1
0 1 1 0
0 0 1 0
0 1 0 0
0 1 1 1
0 1 1 0
0 1 0 0
AB 000 001 011
00
01
11
10
CDE
110111101100010
BE
C D E
A B D
BDABEEDCDECYofformMinimal 
C D E

62. PROBLEM 20: SIMPLIFY USING K-MAPS


)31,19,11,3(can writeWe
),,,,(
T
decbaabcdedecbadecbaedcbafT
ABCDEDECBDECAYofformMinimal 
0 0 1 0
0 0 1 0
0 0 0 0
0 0 1 0
0 0 0 0
0 0 0 0
0 0 1 0
0 0 0 0
AB 000 001 011
00
01
11
10
CDE
110111101100010
B C D E
A C D E
ABCDE

63. PROBLEM 21: SIMPLIFY USING K-MAPS
 )27,26,25,24,19,18,17,16,14,12,11,10,9,8,6,4,2,0(),,,,( MEDCBAf
))()(( CBCAEAYofformMinimal 
0 1 1 0
0 0 0 0
0 0 0 0
0 0 0 0
0 1 1 0
0 1 1 0
1 1 1 1
1 1 1 1
AB 000 001 011
00
01
11
10
CDE
110111101100010
B +C (EPI)
A +C (EPI)
A +E (EPI)
C+E (PI)

64.  d)c,b,f(a,GthatShow  )15,13,10,8,7,5,2,0(
 )14,12,11,9,6,4,3,1(Gofcomplementtheis
equations.2theofnaturecomplementtheillustratetomap-KaUse
1 0 0 1
0 1 1 0
0 1 1 0
1 0 0 1
AB 00 01 11 10
00
01
11
10
CD
1 0 0 1
0 1 1 0
0 1 1 0
1 0 0 1
AB 00 01 11 10
00
01
11
10
CD
DB
DBBDG


DB
DBDBGsGrouping

 ))((,'0
PROBLEM 22:

65. INCOMPLETELY SPECIFIED FUNCTIONS(DON’T CARE TERMS)
When an O/P is not known for
every combination of I/P variables,
the function is said to be
incompletely specified.
Eg. BCD (B3B2B1B0)
to Excess-3 BCD (X3X2X1X0)
Code Converter
B3 B2 B1 B0 X3 X2 X1 X0
0 0 0 0 0 0 1 1
0 0 0 1 0 1 0 0
0 0 1 0 0 1 0 1
0 0 1 1 0 1 1 0
0 1 0 0 0 1 1 1
0 1 0 1 1 0 0 0
0 1 1 0 1 0 0 1
0 1 1 1 1 0 1 0
1 0 0 0 1 0 1 1
1 0 0 1 1 1 0 0
1 0 1 0 X X X X
1 0 1 1 X X X X
1 1 0 0 X X X X
1 1 0 1 X X X X
1 1 1 0 X X X X
1 1 1 1 X X X X

66. 1 0 1 0
1 0 1 0
x x x x
1 0 x x
BCD (B3B2B1B0) to Excess-3 BCD (X3X2X1X0) Code Converter eg.
We have 4 O/Ps here & hence we need to get 4 expressions.
1 0 0 1
1 0 0 1
x x x x
1 0 x x
B3B2
00 01 11 10
00
01
11
10
00 BX 
B1B0
2) K-map for X1
B3B2
00 01 11 10
00
01
11
10
B1B0
0101011 BBBBBBX 
1) K-map for X0

67. 0 0 0 0
0 1 1 1
x x x x
1 1 x x
0 1 1 1
1 0 0 0
x x x x
0 1 x x
B3B2
00 01 11 10
00
01
11
10
)10(2
)01(2)10(2
01202122
BBB
BBBBBB
BBBBBBBX



B1B0
4) K-map for X3
B3B2
00 01 11 10
00
01
11
10
B1B0
120233 BBBBBX 
BCD (B3B2B1B0) to Excess-3 BCD (X3X2X1X0) Code Converter eg.
3) K-map for X2

68. 0 0 1 1
1 1 0 0
0 1 1 0
X X X X
00 01 11 10
00
01
11
10
B1B0
Simplify using K-maps
 
 


)10,8,7,5,0()15,14,13,11,4,2,1(),,,()2
)11,10,9,8()15,13,5,4,3,2(),,,()1
dmDCBAf
dmDCBAfV
CBAADCBV 
X 1 0 1
1 X X 0
0 1 1 1
X 0 1 X
00 01 11 10
00
01
11
10
B1B0
B3B2 B3B2
DBACBDCAf 

69. Simplify using K-maps
 
 


)28,24,14,10()30,26,23,21,8,7,5(),,,,()2
)26,24,10,8(30,28,27,25,22,20,19,17,14,12,11,9,6,4,3,1(),,,,()1
dMEDCBAf
dmEDCBAf
ECECV  ))()(( HFEHGEHFEf 
0 1 1 0
X 1 1 X
X 1 1 X
0 1 1 0
1 0 0 1
1 0 0 1
1 0 0 1
1 0 0 1
AB 000 001 011
00
01
11
10
CDE
110111101100010
1 1 1 1
0 1 1 X
X 1 1 0
1 1 1 1
1 0 0 1
1 1 1 X
X 1 1 0
1 0 0 1
DE 000 001 011
00
01
11
10
FGH
110111101100010
)( HFE  )( HGE 
)( HFE EC EC

70. PROBLEMS ON CIRCUIT DESIGN

71. PROBLEMS ON DESIGN
1) Design a logic circuit which has a single O/P variable z which
is to be true when I/P variables a & b are true or when b is
false but a & c are true.
a b c Z
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
OPCanonicalSabccabcbaz 
0 0 0 0
0 1 1 1
00 01 11 10
0
1
a
bc
)( bcaz
SOPMinimalabacz


a
b
c
z

72. 2) Design a logic circuit whose O/P is to be true when the value
if I/P s exceeds 3. The weighting for each I/P variable is as
follows.
w=3, x=3, y=2, z=1. (Left as an exercise)
3) Design a logic circuit that controls the passage of a signal ‘A’
according to the following requirement.
i. O/P ‘X’ will = ‘A’ when control I/Ps B & C are the same.
ii. ‘X’ will remain ‘HIGH’ when B & C are different.
Implement the ckt using suitable gates.
PROBLEMS ON DESIGN
A B C X
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
0 0 1
1 1 1 1
00 01 11 10
0
1
a
bc
CBAX 
A
B
C
X

73. 1. Difficult to use when no. of variables is > 6.
2. The recognition of groups that form EPI’s becomes
difficult for large K-maps.
3. The technique does not involve a systematic
algorithmic procedure that is suitable for computers.
Since it is a manual technique, simplification
process depends on human abilities.