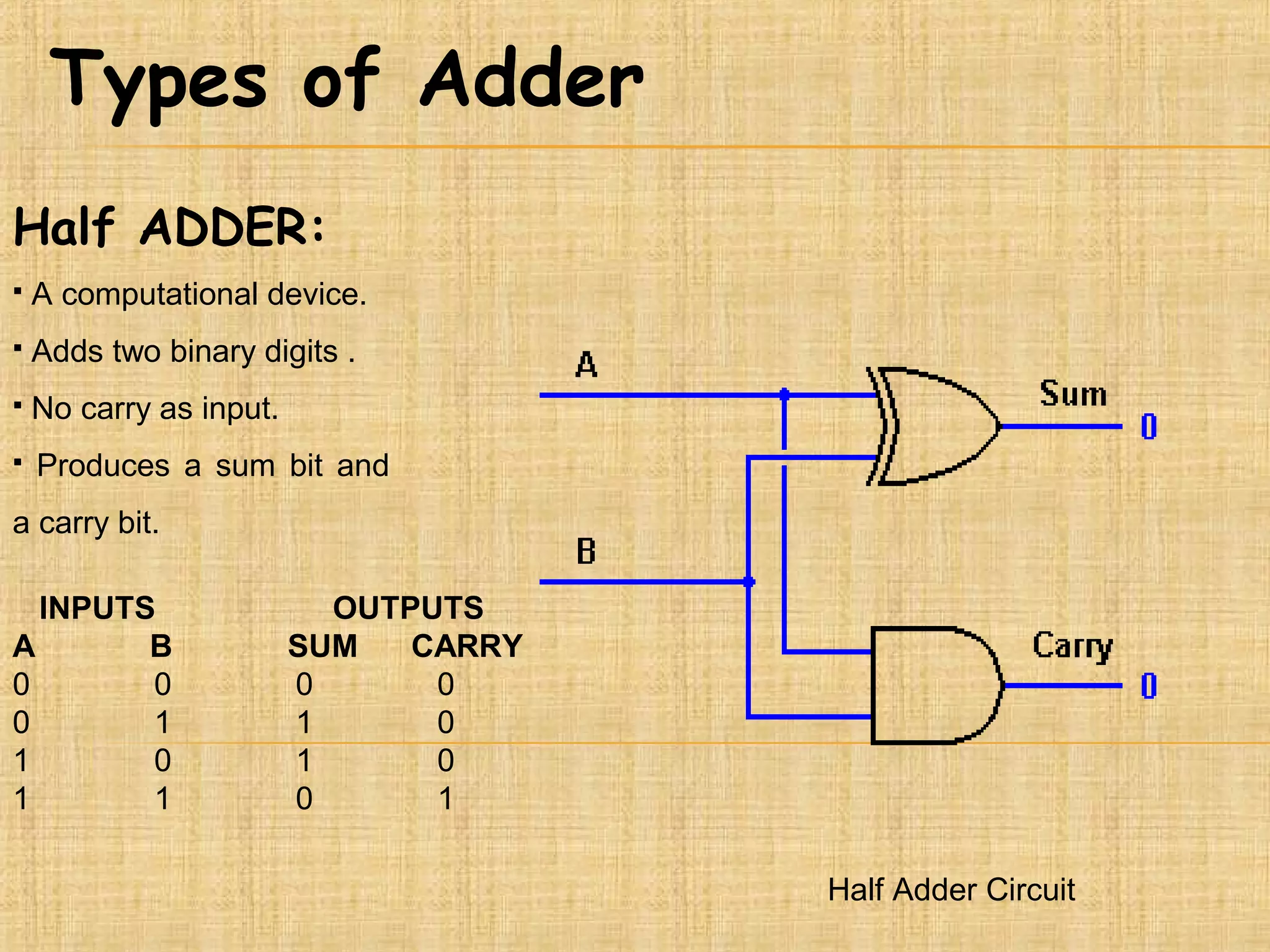
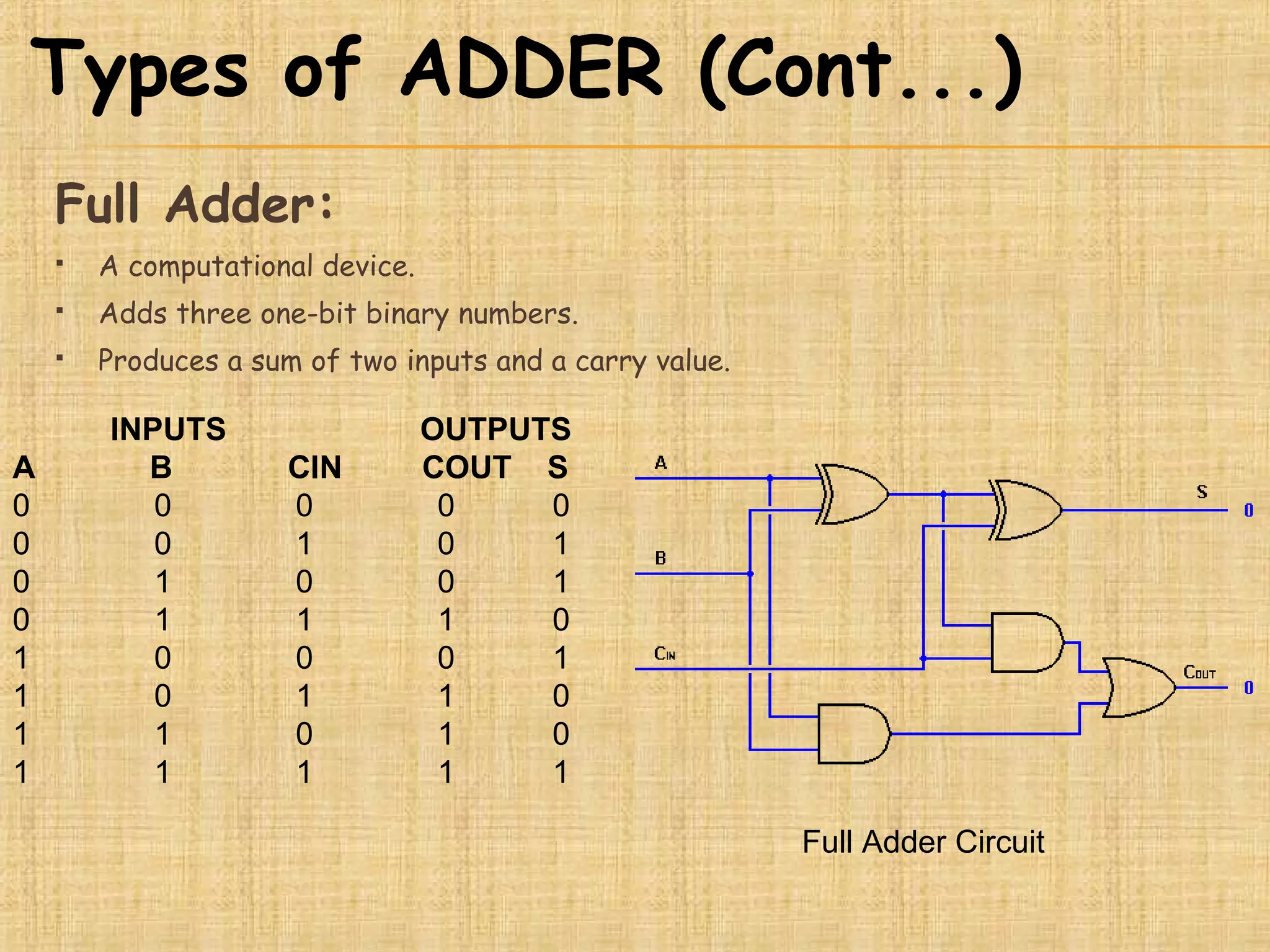
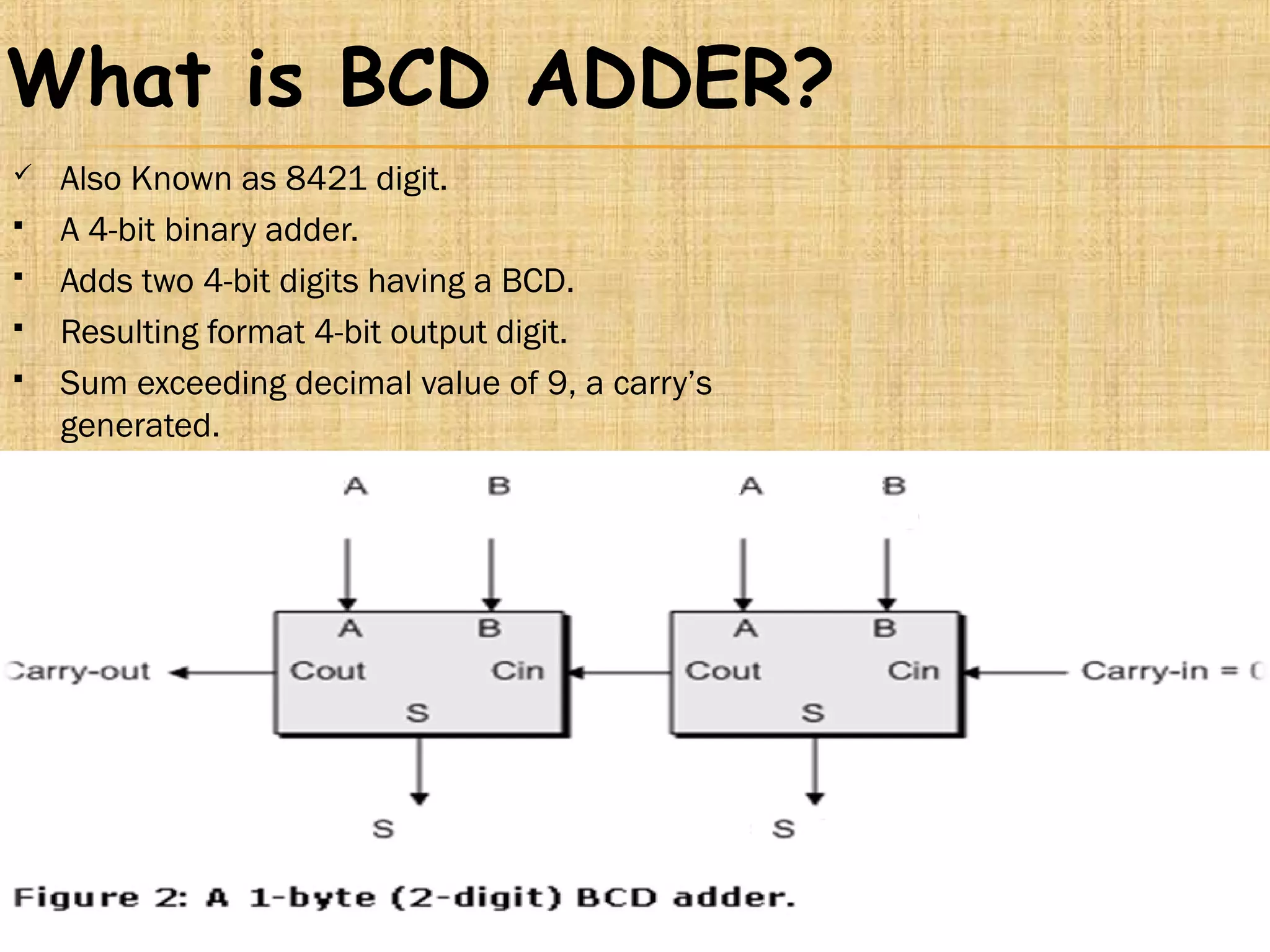
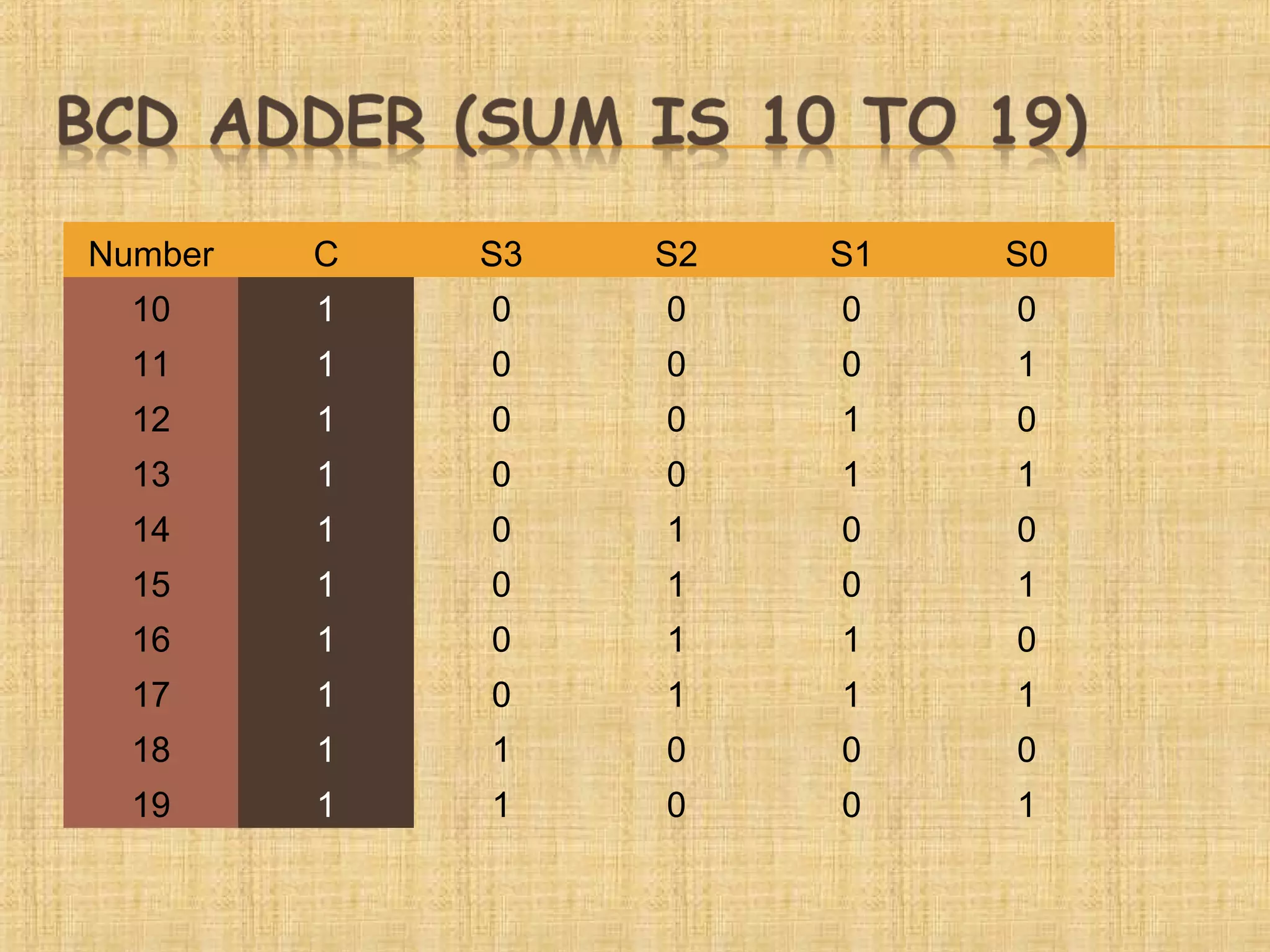
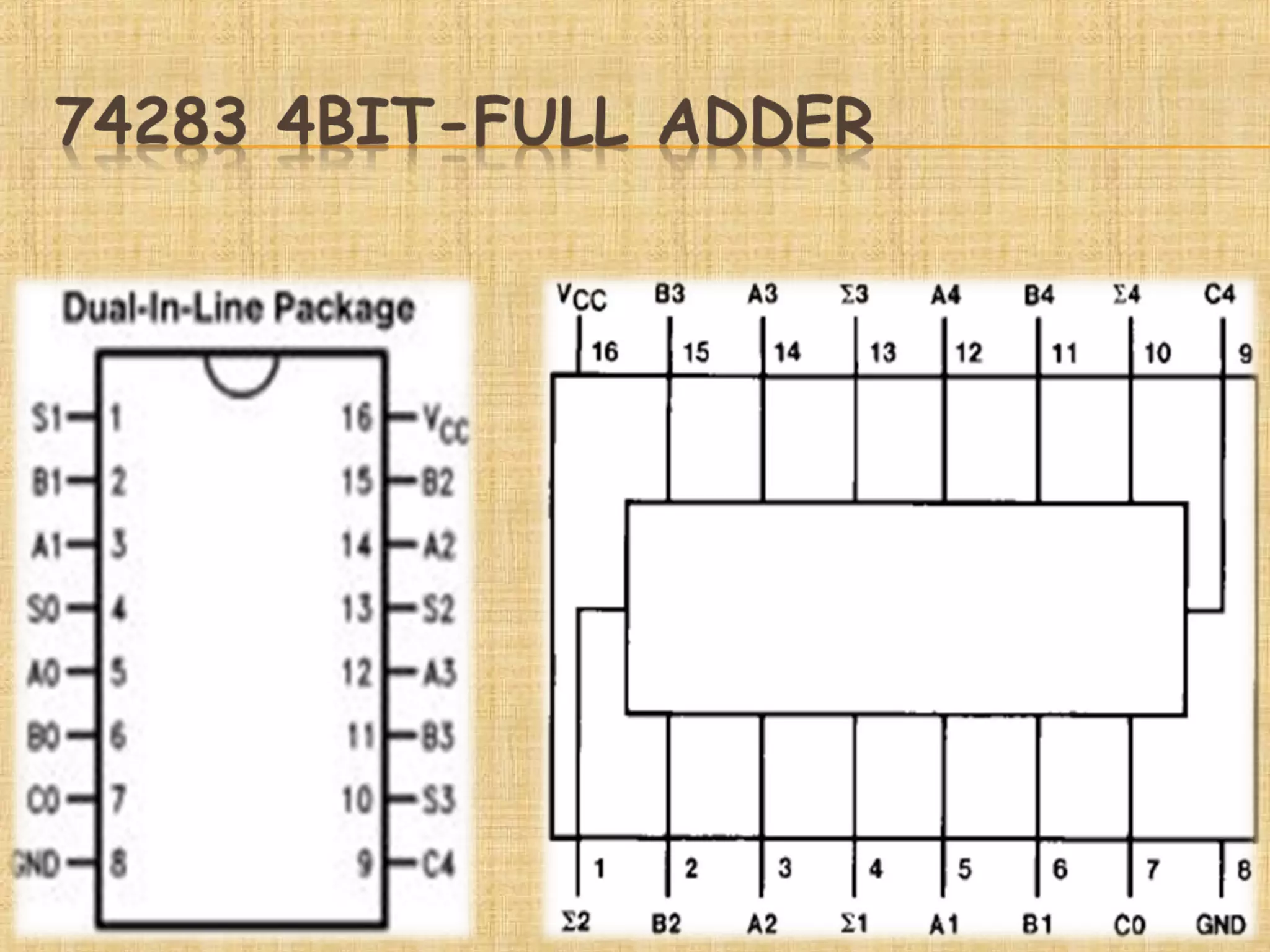
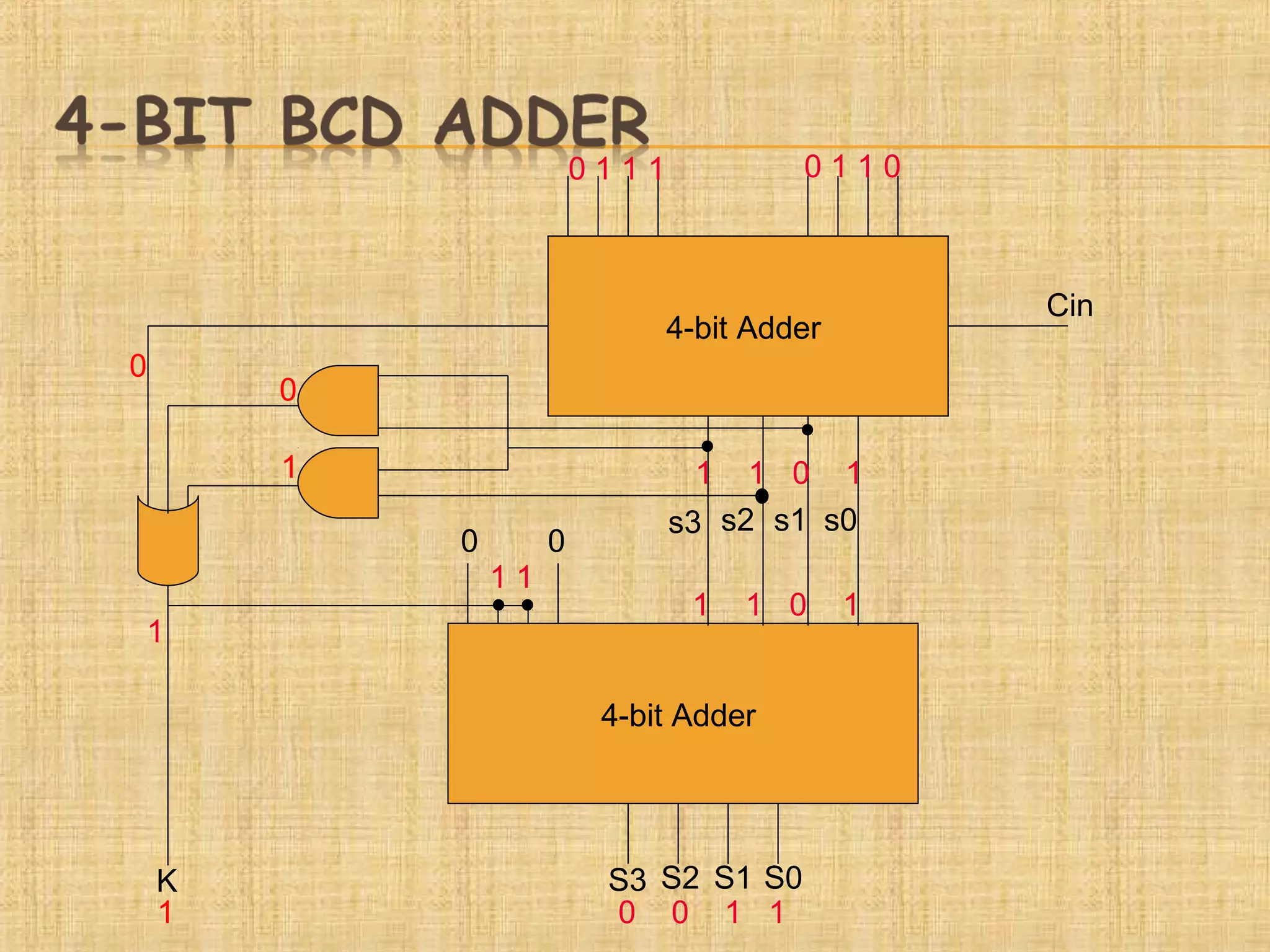
This document presents information about adders and binary coded decimal (BCD) adders. It defines half adders and full adders, which are computational devices that add binary digits and produce sum and carry outputs. It also explains what a BCD adder is and how it adds two 4-bit BCD digits while handling carries such that the result is always a valid BCD number between 0-9. The document provides examples of BCD addition and conversions between binary and BCD formats. It concludes with some applications of BCD adders in areas like digital displays and counters.

1. Welcome
To
Our presentation
Presented by
Shahriar Reza Rusel
ID-011132065
Samrin Ahmed Riya
ID-011142021
Rayhan Ahamed
ID-011142141
Rakib Hasan Suvo
ID-011142016
Dept-CSE

3.  A digital circuit.
 Sums the amplitudes of two input signals.
Representation of Adders:
 Binary-Coded-Decimal or Excess-3
Processor Use:
 Calculate addresses, table indices and
similar operations.
What is ADDER ?

4. Types of Adder

5. Half ADDER:
 A computational device.
 Adds two binary digits .
 No carry as input.
 Produces a sum bit and
a carry bit.
Types of Adder
INPUTS OUTPUTS
A B SUM CARRY
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
Half Adder Circuit

6. Full Adder:
 A computational device.
 Adds three one-bit binary numbers.
 Produces a sum of two inputs and a carry value.
Types of ADDER (Cont...)
INPUTS OUTPUTS
A B CIN COUT S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1
Full Adder Circuit

7.  Also Known as 8421 digit.
 A 4-bit binary adder.
 Adds two 4-bit digits having a BCD.
 Resulting format 4-bit output digit.
 Sum exceeding decimal value of 9, a carry’s
generated.
What is BCD ADDER?

8. Conversion and Coding
 (12)10
1100 00010010Conversion
Coding
(using BCD code
for each digit)

9.  A 4-bit BCD code’s used to represent 0 to 9 digits.
 Adding BCD numbers using BCD addition.
 Adding 6 with the sum while exceeding 9 and generating a carry.
 By adding 6 to the sum, make an invalid digit valid.
.

10. Maximum sum is 9+9 + 1 = 19
Max digit Carry from previous digits

11. Number C S3 S2 S1 S0
0 0 0 0 0 0
1 0 0 0 0 1
2 0 0 0 1 0
3 0 0 0 1 1
4 0 0 1 0 0
5 0 0 1 0 1
6 0 0 1 1 0
7 0 0 1 1 1
8 0 1 0 0 0
9 0 1 0 0 1

12. Number C S3 S2 S1 S0
10 1 0 0 0 0
11 1 0 0 0 1
12 1 0 0 1 0
13 1 0 0 1 1
14 1 0 1 0 0
15 1 0 1 0 1
16 1 0 1 1 0
17 1 0 1 1 1
18 1 1 0 0 0
19 1 1 0 0 1

13. BCD adder sum Binary sum
Number
C S3 S2 S1 S0
10 1 0 0 0 0
11 1 0 0 0 1
12 1 0 0 1 0
13 1 0 0 1 1
14 1 0 1 0 0
15 1 0 1 0 1
16 1 0 1 1 0
17 1 0 1 1 1
18 1 1 0 0 0
19 1 1 0 0 1
K s3 s2 s1 s0
0 1 0 1 0
0 1 0 1 1
0 1 1 0 0
0 1 1 0 1
0 1 1 1 0
0 1 1 1 1
1 0 0 0 0
1 0 0 0 1
1 0 0 1 0
1 0 0 1 1
+6

14.  If sum is up to 9
 Use the regular Adder.
 If the sum > 9
 Use the regular adder and add 6 to the result

15.  Sum of two BCD digits exceeding 9.
 A carry is generated.
 Converting the invalid digit into valid digit.
 Carry generated by adding 6 to the invalid BCD digit’s
passed on to the next BCD digit.

16. Binary sum
Number
K S3 S2 S1 S0
10 0 1 0 1 0
11 0 1 0 1 1
12 0 1 1 0 0
13 0 1 1 0 1
14 0 1 1 1 0
15 0 1 1 1 1
16 1 0 0 0 0
17 1 0 0 0 1
18 1 0 0 1 0
19 1 0 0 1 1
C = K +

17. Binary sum
Number
K S3 S2 S1 S0
10 0 1 0 1 0
11 0 1 0 1 1
12 0 1 1 0 0
13 0 1 1 0 1
14 0 1 1 1 0
15 0 1 1 1 1
16 1 0 0 0 0
17 1 0 0 0 1
18 1 0 0 1 0
19 1 0 0 1 1
C = K + S3*S2+

18. Binary sum
Number
K S3 S2 S1 S0
10 0 1 0 1 0
11 0 1 0 1 1
12 0 1 1 0 0
13 0 1 1 0 1
14 0 1 1 1 0
15 0 1 1 1 1
16 1 0 0 0 0
17 1 0 0 0 1
18 1 0 0 1 0
19 1 0 0 1 1
C = K + S3*S2+
S3*S1

20. 4-bit Adder
4-bit Adder
0 0
s3 s2 s1 s0
S3 S2 S1 S0
Cin
K
0 1 1 00 1 1 1
1 1 0 1
0
1 1 0 1
1 1
1
0 0 1 1
1
0
1

21.  Applications in Decimal Number Display.
 Systematic running of counters.
 Organized digital clocks.

22.  http://www.electronics-
tutorials.ws/combination/comb_7.html
 http://www.encyclopedia.com/doc/1O11-
binarycodeddecimal.html
 http://www2.elo.utfsm.cl/~lsb/elo211/aplicaci
ones/katz/chapter5/chapter05.doc4.html
 https://tams-www.informatik.uni-
hamburg.de/applets/hades/webdemos/20-
arithmetic/10-adders/bcd-adder.html