This document provides an overview of Boolean algebra and logic gates. It introduces Boolean logic operations like AND, OR, and NOT. It covers Boolean algebra laws and De Morgan's theorems. It also discusses logic gate types like AND, OR, NOT, NAND, NOR, XOR and XNOR. Karnaugh maps are introduced as a method to simplify Boolean expressions.

1. IDEAL EYES BUSINESS COLLEGE
A
PRESENTATION
ON
BOOLEAN ALGEBRA
&
LOGIC GATE
PRESENTED TO:- IEBC PRESENTED BY:- VIVEK KUMAR

2. CONTENT
1. INTRODUCTION
2. BOOLEAN LOGIC OPERATION
3. LAWS& RULES OF BOOLEAN ALGEBRA
4. DE MORGAN’S THEOREMS
5. IMPLICATIONS OF DE MORGAN’S
THEOREMS
6. COMBINATIONAL LOGIC
7. KARNAUGH MAPS
8. LOGIC GATE

3. INTRODUCTION
• 1854: Logical algebra was published by George
Boole known today as “Boolean Algebra”
• It’s a convenient way and systematic way of
expressing and analyzing the operation of logic
circuits.
• 1938: Claude Shannon was the first to apply Boole’s
work to the analysis and design of logic circuits.
• A Boolean algebra value can be either true or false.
• Digital logic uses 1 to represent true and 0 to
represent false.

4. BOOLEAN LOGIC OPERATION
 AND OPERATION
OR OPERATION
 NOT (COMPLEMENTATION ) OPERATION

5. AND OPERATION
• It is a two variables cases.
• It is written as Y=A.B.
• Dot (.) symbol is the common symbol of AND
gate.
• When both input are 1 then output is also 1.
• When both and also at list any input 0 then
output is also 0.
• We can also write as Y=AB.

6. AND OPERATION TRUTH TABLE

7. OR OPERATION
• It is also two variables case.
• It is written as Y=A+B.
• Plus (+) symbol is the common symbol of OR
gate.
• When both input are 0 then output is also 0.
• When both input 1 and at list any input 1
then output is also 1.

8. OR OPERATION TRUTH TABLE

9. NOT (COMPLEMENTATION ) OPERATION
•It is one variable case.
•It has only one input.
•It change any input to it’s compliment.
•As like 1 to 0 & 0 to 1.
•It is also written as A=A.
•It is also called inverter.

10. LAWS & RULES OF BOOLEAN
ALGEBRA
OPERATIONS WITH 0 AND 1:
• 1. X + 0 = X 1D. X • 1 = X
• 2. X + 1 = 1 2D. X • 0 = 0
• IDEMPOTENT LAWS
• 3. X + X = X 3D. X • X = X
CONTINUE

11. LAWS & RULES OF BOOLEAN
ALGEBRA
• 4. ( X' ) ' = X
• LAWS OF COMPLEMENTARITY:
• 5. X + X' = 1 5D. X • X' = 0
• COMMUTATIVE LAWS:
• 6. X + Y = Y + X 6D. X • Y = Y • X
CONTINUE

12. LAWS & RULES OF BOOLEAN
ALGEBRA
• COMMUTATIVE LAWS:
• 6. X + Y = Y + X 6D. X • Y = Y • X
• ASSOCIATIVE LAWS:
• 7. (X + Y) + Z = X + (Y + Z) 7D. (XY)Z = X(YZ) = XYZ
• DISTRIBUTIVE LAWS:
• 8. X( Y + Z ) = XY + XZ 8D. X + YZ = ( X + Y ) ( X +
Z )
CONTINUE

13. LAWS & RULES OF BOOLEAN
ALGEBRA
• SIMPLIFICATION THEOREMS:
• 9. X Y + X Y' = X 9D. ( X + Y ) ( X + Y' ) = X
• 10. X + XY = X 10D. X ( X + Y ) = X
• 11. ( X + Y' ) Y = XY 11D. XY' + Y = X + Y
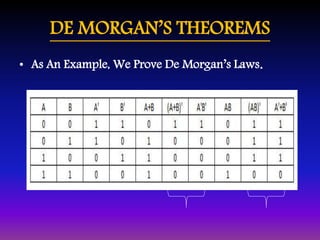
• DEMORGAN’S LAWS:
• 12. ( X + Y + Z + … )' = X'Y'Z'… 12D. (X Y Z …)' = X' + Y' + Z' + …
• 13. [ f ( X1, X2, … XN, 0, 1, +, • ) ]' = f ( X1', X2', … XN', 1, 0, •, + )
CONTINUE

14. IMPLIMANTATION OF DE MORGAN’S
THEOREMS
THEOREM 1
A+B = A.B
A
B
Y=A+B
THEOREM 2
A
B
Y=A.B

15. DE MORGAN’S THEOREMS
• As An Example, We Prove De Morgan’s Laws.

16. COMBINATIONAL LOGIC
 SOME OF PRODUCT (SOP)
 PRODUCT OF SOMS (POS)
HOW TO CHANGE SOP TO POS & POS TO SOP
 CANONICAL FORMS

17. SOME OF PRODUCT (SOP)
• When two or more product terms are summed by
Boolean addition,
• the resulting expression is a sum-of-products (SOP).
Some examples are:
• AB + ABC
• ABC + CDE + BCD
• AB + BCD + AC
• Also, an SOP expression can contain a single-variable
term, as in
• A + ABC + BCD.
.

18. SOME OF PRODUCT (SOP)
• Example
• Convert each of the following Boolean expressions
to SOP form:
• (a) AB + B(CD + EF)

19. PRODUCT OF SOMS (POS)
When two or more sum terms are
multiplied the resulting expression is a
product-of-sums (POS).
Some examples are:-
1 (A + B)(B + C + D)(A + C).
2 (A + B + C)( C + D + E)(B + C + D)
3 (A + B)(A + B + C)(A + C)

20. PRODUCT OF SUMS (POS)
(A+B)(B+C+D)(A+C)

21. HOW TO CHANGE SOP TO POS &
POS TO SOP
• SOP TO POS
EX:- AB + B(CD + EF)
Every (+) Sign Change Into( *) & Every * Sign
Change In to (+) Sign.
Result Will Be
(A+B)(B+C+D)(B+E+F)

22. HOW TO CHANGE SOP TO POS &
POS TO SOP
• POS TO SOP
Ex:- (A+B)(B+C+D)(B+E+F)
Every (*) Sign Change Into( +) & Every (+)Sign
Change In Yo (*) Sign.
Result Will Be
AB + BCD + BEF

23. CANONICAL FORMS
1 To Place A SOP Equation Into Canonical From Using
Boolean Algebra We Do The Following.
 Identify The Missing Variable In Each AND Terms.
 AND the missing terms and its complement with the
original AND term AB(C+C) because C+C =1,the
original AND term value is not changed.
 Expand the term by application of the proparty of
the distribution, ABC+ABC

24. CANONICAL FORMS
2. To Place A POS Equation Into Canonical From Using
Boolean Algebra We Do The Following.
 Identify The Missing Variable In Each OR Terms.
OR the missing terms and its complement with the
original OR term A+B+CC because CC =0,the original
OR term value is not changed.
 Expand the term by application of the proparty of
the distribution, (A+B+C)(A+B+C).

25. CANONICAL FORMS
EX:- Convert A+B To Minterms.
Solution:- A+B = A.1 + B.1
=A(B+B)+B(A+A)
=AB+AB+BA+BA
minterms Y = A+B = AB+AB+BA
maxterms Y = A+B = (A+B)(A+B)(B+A)

26. K-MAPS INTRODUCTION
A Karnaugh map provides a systematic
method for simplifying Boolean
expressions and, if properly used, will
produce the simplest SOP or POS
expression possible, known as the
minimum expression & maximum
expression.

27. K-MAPS INTRODUCTION
Number cells in k-maps depends upon the
number of variables of boolean expression. K-maps
can be used for any number of variables.
But it is used upto six variables beyond which it
is not very convenient,
1. 2-variable map contains 4 cells.
2. 3-variable map contains 8 cells.
3. 4-variable map contains 16 cells.
4. n-variable map contains 2 on power n cells.

28. LOGIC GATE
 AND GATE
OR GATE
 NOT GATE
 NAND GATE
 NOR GATE
 EX-OR GATE
 EX-NOR GATE
 TRUTH TABLE
 LOGIC DIGRAM

29. AND FUNCTION
Output Y is TRUE if inputs A AND
B are TRUE, else it is FALSE.
Text Description 
Logic Symbol 
Truth Table 
Boolean Expression 
AND
A
B
Y
INPUTS OUTPUT
A B Y
0 0 0
0 1 0
1 0 0
1 1 1
AND Gate Truth Table
AND Symbol
Y = A x B = A • B = AB

30. OR FUNCTION
Output Y Is TRUE If Input A OR B Is TRUE or
both are TURE, Else It Is FALSE.
Text Description 
Logic Symbol 
Truth Table 
Boolean Expression  Y = A + B
OR Symbol
A
B
OR Y
INPUTS OUTPUT
A B Y
0 0 0
0 1 1
1 0 1
1 1 1
OR Gate Truth Table

31. NOT FUNCTION (INVERTER)
Output Y Is TRUE If Input A Is FALSE, Else It Is
FALSE. Y Is The Inverse Of A.
Text Description 
Logic Symbol 
Truth Table 
A NOT Y
INPUT OUTPUT
A Y
0 1
1 0
NOT Gate Truth Table
Boolean Expression 
Y = A

32. NAND FUNCTION
Output Y is FALSE if inputs A AND B are TRUE,
else it is TRUE.
Text Description 
Logic Symbol 
Truth Table 
Boolean Expression 
A
B
NAND Y
A bubble is an inverter
This is an AND Gate with an inverted output
INPUTS OUTPUT
A B Y
0 0 1
0 1 1
1 0 1
1 1 0
NAND Gate Truth Table
Y=AB

33. NOR FUNCTION
Output Y is FALSE if input A OR B is TRUE, or
both are TURE, else it is TRUE.
Text Description 
Logic Symbol 
Truth Table 
A
B
NOR Y
Boolean Expression 
A bubble is an inverter.
This is an OR Gate with its output inverted.
INPUTS OUTPUT
A B Y
0 0 1
0 1 0
1 0 0
1 1 0
NOR Gate Truth Table
Y =A+B