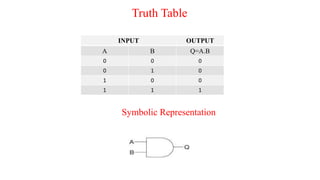
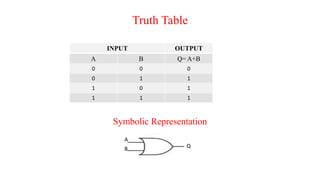
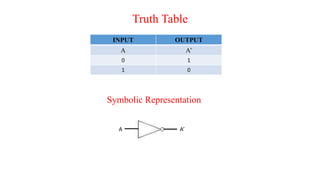
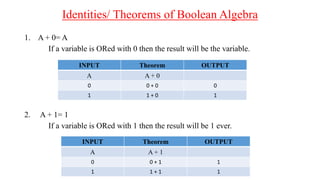
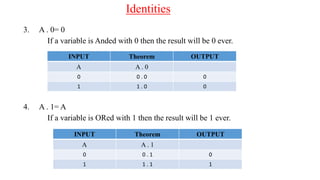
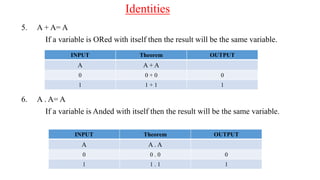
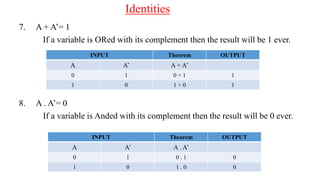
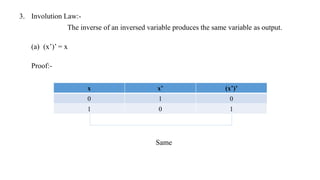
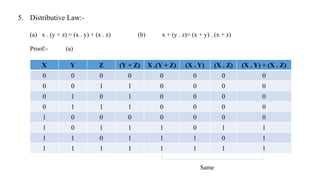
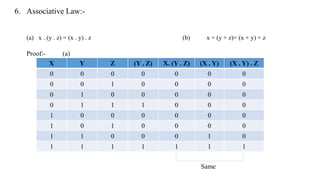
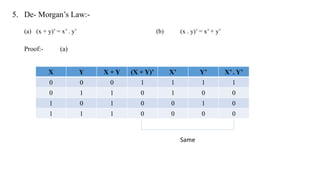
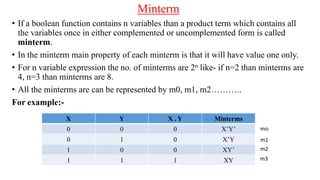
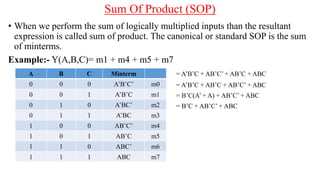
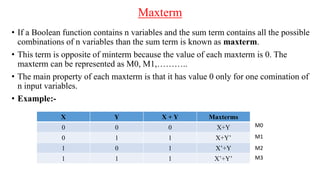
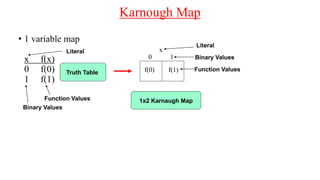
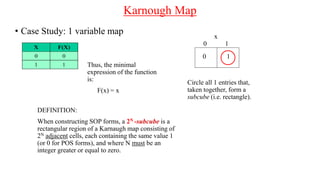
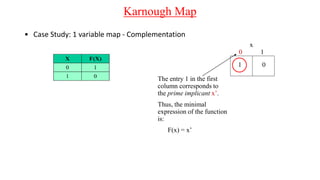
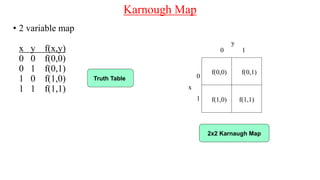
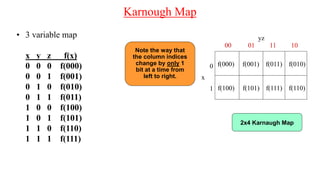
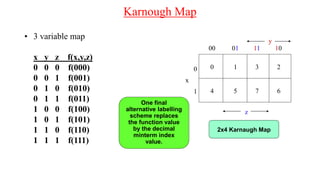
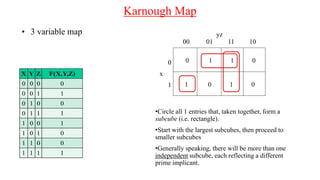
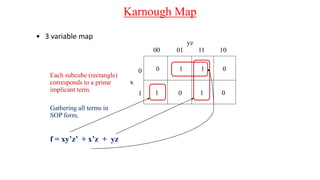
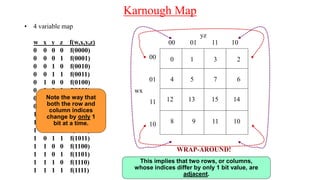
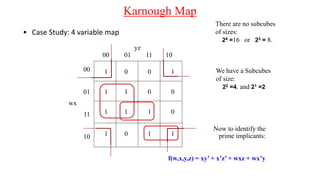
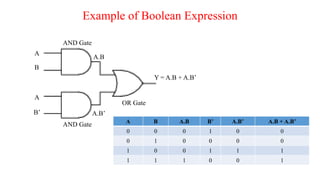
The document discusses Boolean expressions and their use in computer programming. It defines Boolean expressions as expressions that evaluate to true or false. Boolean expressions are composed of logical operators like AND, OR, and NOT. The document then discusses different logical operators and their truth tables. It also covers Boolean algebra identities and theorems. Finally, it introduces concepts like minterms, maxterms, sum of products, and product of sums and how Karnaugh maps can be used to simplify Boolean expressions.

1. MOHAN LAL SUKHADIA UNIVERSITY
Seminar on
“ Boolean Expression “
Presented to: Presented by:
M.K. Jain Sir ----------------
Mrs. Priyanka Soni MCA 1st sem.

2. Introduction of Boolean Expression:
 In computer science, a Boolean expression is an expression in a programing
language that produces a Boolean value when evaluated i.e. one of true or false.
 Boolean expressions are used mostly with while loops, and conditional statements.
Boolean expressions can be contrasted with arithmetic expressions which are
expressions that evaluated to a number.
 Boolean expressions are made up of the three logical operators (AND, OR, NOT),
the relational operator (> >= < = = <>) and functions that return true or false.

3. Logical Operators
• Electricity is the basic element of every digital device. When
electricity flow in a device it is represented by 1. When flow is not
available it is represented by 0.
• To produce the combine results of 2 or more inputs we use
special type of operators called logical operators.

4. Use of Logic Operators/ Logic gates
• Logic gates are used in every digital electronic device.
• The output depends on the gates to which input has been given.
• Several applications are being processed by the help of logic gates,
such as computers, mobiles, USB drives, etc.
For Example:-
1 way- like switches (2 inputs are connected to the plug
than only 1 output is displayed)

5. There are 3 types of operators:
1. Logical AND operator
2. Logical OR operator
3. Logical NOT operator

6. Logical AND operators
• This AND operator is used to produce logical multiplication.
• This is represented by dot (.), and (&&).
• This operator produces true result only when both the member inputs
are in working states (1).
If any of the input member has false value than this will
produce false (0) output.

7. Truth Table
Symbolic Representation
INPUT OUTPUT
A B Q=A.B
0 0 0
0 1 0
1 0 0
1 1 1

8. Logical OR operator
• This OR operator is used to produce logical addition.
• This is represented by plus (+), or (| |).
• This operator produces true result only when one of the input is in
working states (1).
• If both of the inputs are false than this will produce false (0) output.

9. Truth Table
Symbolic Representation
INPUT OUTPUT
A B Q= A+B
0 0 0
0 1 1
1 0 1
1 1 1
A
B Q

10. Logical NOT operator
• It is also called Complement operator.
• This NOT operator is used to produce reverse result.
• This is represented by Desh (’) or Bar(‾).
• This operator produces true(1) result if input is false(0).
• If the inputs is true(1) than this will produce false(0) output.

11. Truth Table
INPUT OUTPUT
A A’
0 1
1 0
Symbolic Representation
A A’

12. Basic Identities of Boolean Algebra
• The Boolean algebra contains different identities which are also
called theorems. These theorems are based on the logical operators.
• If we use logical OR in the identity, then the operation is called
‘Oring’ and if we use AND in an operation then the operation is called
‘Anding’.

13. Identities/ Theorems of Boolean Algebra
1. A + 0= A
If a variable is ORed with 0 then the result will be the variable.
2. A + 1= 1
If a variable is ORed with 1 then the result will be 1 ever.
INPUT Theorem OUTPUT
A A + 0
0 0 + 0 0
1 1 + 0 1
INPUT Theorem OUTPUT
A A + 1
0 0 + 1 1
1 1 + 1 1

14. 3. A . 0= 0
If a variable is Anded with 0 then the result will be 0 ever.
4. A . 1= A
If a variable is ORed with 1 then the result will be 1 ever.
INPUT Theorem OUTPUT
A A . 0
0 0 . 0 0
1 1 . 0 0
INPUT Theorem OUTPUT
A A . 1
0 0 . 1 0
1 1 . 1 1
Identities

15. 5. A + A= A
If a variable is ORed with itself then the result will be the same variable.
6. A . A= A
If a variable is Anded with itself then the result will be the same variable.
INPUT Theorem OUTPUT
A A + A
0 0 + 0 0
1 1 + 1 1
INPUT Theorem OUTPUT
A A . A
0 0 . 0 0
1 1 . 1 1
Identities

16. 7. A + A’= 1
If a variable is ORed with its complement then the result will be 1 ever.
8. A . A’= 0
If a variable is Anded with its complement then the result will be 0 ever.
INPUT Theorem OUTPUT
A A’ A + A’
0 1 0 + 1 1
1 0 1 + 0 1
INPUT Theorem OUTPUT
A A’ A . A’
0 1 0 . 1 0
1 0 1 . 0 0
Identities

17. Laws of Boolean Algebra
1. Idempotent Law:
(a) x + x= x (b) x .x= x
Proof:- Proof:-
= x+ x = x . x
= (x + x).1 = x . x+ 0
= (x + x).(x + x’) = x . x + x . x’
= x + x + x . x’+ x . x’ = x . (x + x’)
= x + 0 = x . 1
= x = x

18. 2. Absorption Law:
(a) x + x . y = x (b) x . (x + y)= x
Proof:- Proof:-
= x+ x . y = x . (x + y)
= x . 1 + x . y = x . x + x . y
= x . (1 + y) = x + x . y
= x . (y + 1) = x . (1 + y)
= x .1 = x . 1
= x = x

19. 3. Involution Law:-
The inverse of an inversed variable produces the same variable as output.
(a) (x’)’ = x
Proof:-
Same
x x’ (x’)’
0 1 0
1 0 1

20. 4. Commutative Law:-
The addition of 2 variables does not effect by their order. This law is
called commutative law.
(a) x + y = y + x (b) x . y = y . x
Proof:- proof:-
Same Same
X Y X + Y Y + X
0 0 0 0
0 1 1 1
1 0 1 1
1 1 1 1
X Y X . Y Y . X
0 0 0 0
0 1 0 0
1 0 0 0
1 1 1 1

21. 5. Distributive Law:-
(a) x . (y + z) = (x . y) + (x . z) (b) x + (y . z)= (x + y) . (x + z)
Proof:- (a)
Same
X Y Z (Y + Z) X .(Y + Z) (X . Y) (X . Z) (X . Y) + (X . Z)
0 0 0 0 0 0 0 0
0 0 1 1 0 0 0 0
0 1 0 1 0 0 0 0
0 1 1 1 0 0 0 0
1 0 0 0 0 0 0 0
1 0 1 1 1 0 1 1
1 1 0 1 1 1 0 1
1 1 1 1 1 1 1 1

22. 6. Associative Law:-
(a) x . (y . z) = (x . y) . z (b) x + (y + z)= (x + y) + z
Proof:- (a)
Same
X Y Z (Y . Z) X. (Y . Z) (X . Y) (X . Y) . Z
0 0 0 0 0 0 0
0 0 1 0 0 0 0
0 1 0 0 0 0 0
0 1 1 1 0 0 0
1 0 0 0 0 0 0
1 0 1 0 0 0 0
1 1 0 0 0 1 0
1 1 1 1 1 1 1

23. 5. De- Morgan’s Law:-
(a) (x + y)’ = x’ . y’ (b) (x . y)’ = x’ + y’
Proof:- (a)
Same
X Y X + Y (X + Y)’ X’ Y’ X’ . Y’
0 0 0 1 1 1 1
0 1 1 0 1 0 0
1 0 1 0 0 1 0
1 1 1 0 0 0 0

24. Minimization Techniques
The techniques which are used minimize the variables or gates in
a logical expression are called minimization techniques.
The most commonly used minimization techniques are:-
1. Using Boolean Theorms
2. Using Karnough Map
3. Using Quine Macluskey Method(Tabular method)
4. Using Variable Mapping Method

25. Minterm
• If a boolean function contains n variables than a product term which contains all
the variables once in either complemented or uncomplemented form is called
minterm.
• In the minterm main property of each minterm is that it will have value one only.
• For n variable expression the no. of minterms are 2n like- if n=2 than minterms are
4, n=3 than minterms are 8.
• All the minterms are can be represented by m0, m1, m2………..
For example:-
X Y X . Y Minterms
0 0 0 X’Y’
0 1 0 X’Y
1 0 0 XY’
1 1 1 XY
mo
m1
m2
m3

26. Sum Of Product (SOP)
• When we perform the sum of logically multiplied inputs than the resultant
expression is called sum of product. The canonical or standard SOP is the sum
of minterms.
Example:- Y(A,B,C)= m1 + m4 + m5 + m7
= A’B’C + AB’C’ + AB’C + ABC
= A’B’C + AB’C + AB’C’ + ABC
= B’C(A’ + A) + AB’C’ + ABC
= B’C + AB’C’ + ABC
A B C Minterm
0 0 0 A’B’C’ m0
0 0 1 A’B’C m1
0 1 0 A’BC’ m2
0 1 1 A’BC m3
1 0 0 AB’C’ m4
1 0 1 AB’C m5
1 1 0 ABC’ m6
1 1 1 ABC m7

27. Maxterm
• If a Boolean function contains n variables and the sum term contains all the possible
combinations of n variables than the sum term is known as maxterm.
• This term is opposite of minterm because the value of each maxterm is 0. The
maxterm can be represented as M0, M1,………..
• The main property of each maxterm is that it has value 0 only for one comination of
n input variables.
• Example:-
X Y X + Y Maxterms
0 0 0 X+Y
0 1 1 X+Y’
1 0 1 X’+Y
1 1 1 X’+Y’
M0
M1
M2
M3

28. Product Of Sum (POS)
• The product of sum can be difined as the logical product of the maxterm for
which it has the value 0.
Example:- f(A,B,C)= (A’+B’+C) . (A+C) . (A’+B’)
= (A’+B’+C) . (A+C+BB’) . (A’+B’+CC’)
= (A’+B’+C) . ((A+C)+BB’) . ((A’+B’)+CC’)
By appling: x+y . z= (x+y) . (x+z)
= (A’+B’+C) . (A+C+B) . (A+C+B’) . (A’+B’+C) . (A’+B’+C’)
= M6, M0, M2, M6, M7
= M0, M2. M6, M7

29. Karnough Map (K- map)
• Some times the Boolean theorems and laws makes the simplification logics of Boolean
functions more complex. Than we have to use the k-map techniques.
• It is a graphical method which is used to simplify a Boolean function or to convert a truth
table into its equalent logic circuit.
• The k-map is designed by squares where each square represents a minterm or maxterm.
• We will determine these techniques by studying examples in order to establish the rules for
map manipulation.

30. Karnough Map
• 1 variable map
x f(x)
0 f(0)
1 f(1)
f(0) f(1)
x
0 1
Truth Table
Literal
Binary Values
Function Values
Literal
Binary Values
Function Values 1x2 Karnaugh Map

31. Karnough Map
• Case Study: 1 variable map
0 1
x
0 1
Circle all 1 entries that,
taken together, form a
subcube (i.e. rectangle).
DEFINITION:
When constructing SOP forms, a 2N -subcube is a
rectangular region of a Karnaugh map consisting of
2N adjacent cells, each containing the same value 1
(or 0 for POS forms), and where N must be an
integer greater or equal to zero.
Thus, the minimal
expression of the function
is:
F(x) = x

32. Karnough Map
• Case Study: 1 variable map - Complementation
1 0
x
0 1
The entry 1 in the first
column corresponds to
the prime implicant x’.
Thus, the minimal
expression of the function
is:
F(x) = x’

33. Karnough Map
• 2 variable map
x y f(x,y)
0 0 f(0,0)
0 1 f(0,1)
1 0 f(1,0)
1 1 f(1,1)
f(0,0)
y
0 1
0
x
1 f(1,0)
f(0,1)
f(1,1)
Truth Table
2x2 Karnaugh Map

34. Karnough Map
• 3 variable map
x y z f(x)
0 0 0 f(000)
0 0 1 f(001)
0 1 0 f(010)
0 1 1 f(011)
1 0 0 f(100)
1 0 1 f(101)
1 1 0 f(110)
1 1 1 f(111)
f(000) f(001) f(011) f(010)
yz
00 01 11 10
0
x
1 f(100) f(101) f(111) f(110)
2x4 Karnaugh Map
Note the way that
the column indices
change by only 1
bit at a time from
left to right.

35. Karnough Map
• 3 variable map
x y z f(x,y,z)
0 0 0 f(000)
0 0 1 f(001)
0 1 0 f(010)
0 1 1 f(011)
1 0 0 f(100)
1 0 1 f(101)
1 1 0 f(110)
1 1 1 f(111)
0 1 3 2
y
00 01 11 10
0
x
1 4 5 7 6
2x4 Karnaugh Map
One final
alternative labelling
scheme replaces
the function value
by the decimal
minterm index
value.
z

36. Karnough Map
• 3 variable map
0 1 1 0
yz
00 01 11 10
0
x
1 1 0 1 0
•Circle all 1 entries that, taken together, form a
subcube (i.e. rectangle).
•Start with the largest subcubes, then proceed to
smaller subcubes
•Generally speaking, there will be more than one
independent subcube, each reflecting a different
prime implicant.

37. Karnough Map
• 3 variable map
0 1 1 0
yz
00 01 11 10
0
x
1 1 0 1 0
Each subcube (rectangle)
corresponds to a prime
implicant term.
Gathering all terms in
SOP form,
f = xy’z’ + x’z + yz

38. Karnough Map
• 4 variable map
w x y z f(w,x,y,z)
0 0 0 0 f(0000)
0 0 0 1 f(0001)
0 0 1 0 f(0010)
0 0 1 1 f(0011)
0 1 0 0 f(0100)
0 1 0 1 f(0101)
0 1 1 0 f(0110)
0 1 1 1 f(0111)
1 0 0 0 f(1000)
1 0 0 1 f(1001)
1 0 1 0 f(1010)
1 0 1 1 f(1011)
1 1 0 0 f(1100)
1 1 0 1 f(1101)
1 1 1 0 f(1110)
1 1 1 1 f(1111)
f(0000) f(0001) f(0011) f(0010)
yz
00 01 11 10
00
01
wx
11
10 f(1000) f(1001) f(1011) f(1010)
f(0100) f(0101) f(0111) f(0110)
f(1100) f(1101) f(1111) f(1110)

39. Karnough Map
• 4 variable map
w x y z f(w,x,y,z)
0 0 0 0 f(0000)
0 0 0 1 f(0001)
0 0 1 0 f(0010)
0 0 1 1 f(0011)
0 1 0 0 f(0100)
0 1 0 1 f(0101)
0 1 1 0 f(0110)
0 1 1 1 f(0111)
1 0 0 0 f(1000)
1 0 0 1 f(1001)
1 0 1 0 f(1010)
1 0 1 1 f(1011)
1 1 0 0 f(1100)
1 1 0 1 f(1101)
1 1 1 0 f(1110)
1 1 1 1 f(1111)
Note the way that
both the row and
column indices
change by only 1
bit at a time.
0 1 3 2
yz
00 01 11 10
00
01
wx
11
10
4 5 7 6
12 13 15 14
8 9 11 10
This implies that two rows, or columns,
whose indices differ by only 1 bit value, are
adjacent.
WRAP-AROUND!

40. Karnough Map
• Case Study: 4 variable map
1 0 0 1
yz
00 01 11 10
00
01
wx
11
10
1 1 0 0
1 1 1 0
1 0 1 1
Now to identify the
prime implicants:
f(w,x,y,z) = xy’ + x’z’ + wxz + wx’y
There are no subcubes
of sizes:
24 =16 or 23 = 8.
We have a Subcubes
of size:
22 =4. and 21 =2

41. Example of Boolean Expression
Y = A.B + A.B’
AND Gate
AND Gate
OR Gate
A.B
A.B’
A
B
A
B’
A B A.B B’ A.B’ A.B + A.B’
0 0 0 1 0 0
0 1 0 0 0 0
1 0 0 1 1 1
1 1 1 0 0 1

42. Conclusion
• We have studied and developed several techniques for simplifying Boolean
expressions.
• These are based on the axioms, definitions and theorems of the Boolean
Algebra, applied through the Boolean Calculus.
• Powerful tabular techniques have been developed for rapid reduction to some
minimal cost forms using
• Karnaugh maps
• An even more powerful technique has been developed by Quine and
McCluskey (and Petrick).