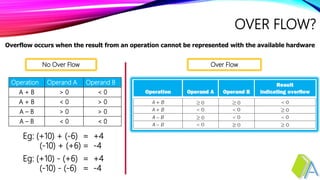
The document discusses the concepts of signed and unsigned arithmetic, specifically focusing on addition and subtraction operations in computer systems. It explains overflow conditions that occur when the result of an arithmetic operation exceeds the representable range of the hardware. Examples are provided to demonstrate scenarios of overflow and underflow with various integer values.

1. ADDITION & SUBTRACTION
Un Signed Arithmetic Signed Arithmetic
add
addi
sub
The MIPS recognizes or ignores overflow by two kinds of arithmetic instructions
addu
addui
subu
cause exceptions on overflowdo not cause exceptions on overflow

2. OVER FLOW?
No Over Flow Over Flow
Overflow occurs when the result from an operation cannot be represented with the available hardware
Operation Operand A Operand B
A + B > 0 < 0
A + B < 0 > 0
A – B > 0 > 0
A – B < 0 < 0
Eg: (+10) + (-6) = +4
(-10) + (+6) = -4
Eg: (+10) - (+6) = +4
(-10) - (-6) = -4

3. OVER FLOW?
Over Flow
Overflow occurs when the result from an operation cannot be represented with the available hardware
Addition
10000
+10 01010
+6 00110 (+)
Over Flow
10111
-5 1011
-4 1100 (+)
Over Flow

4. OVER FLOW?
Over Flow
Overflow occurs when the result from an operation cannot be represented with the available hardware
Subtraction
11100
+6 00110
-10 10110 (-)
Over Flow
0110
-6 1010
+4 0100 (-)
Over Flow

5. EXAMPLE
Assume 185 and 122 are unsigned 8-bit decimal integers. Calculate 185 – 122. Is
there over flow, under flow, or neither?
10111001
01111010 (-)
185
122
11
0
1 1
1
010
1
0 110
1
1
110
10
Neither Over Flow nor Under FlowOperation Operand A Operand B
A + B > 0 < 0
A + B < 0 > 0
A – B > 0 > 0
A – B < 0 < 0
Computer Organization and Design by David A Patterson – Page no. 237
Condition for No Over Flow

6. EXAMPLE
Assume 185 and 122 are signed 8-bit decimal integers stored in sign-magnitude
format. Calculate 185 + 122. Is there over flow, under flow, or neither?
10111001
01111010 +122 (+)
185
122
1100110
Neither Over Flow nor Under Flow
-57
1111
10
Operation Operand A Operand B
A + B > 0 < 0
A + B < 0 > 0
A – B > 0 > 0
A – B < 0 < 0
Computer Organization and Design by David A Patterson – Page no. 237
Condition for No Over Flow

7. EXAMPLE
Assume 185 and 122 are signed 8-bit decimal integers stored in sign-magnitude
format. Calculate 185 - 122. Is there over flow, under flow, or neither?
10111001
01111010 +122 (-)
185
122
1111110 Over Flow
-57
0
Computer Organization and Design by David A Patterson – Page no. 237