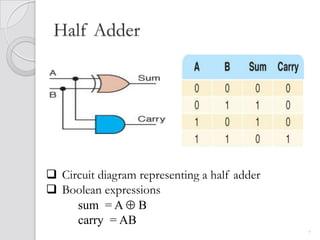
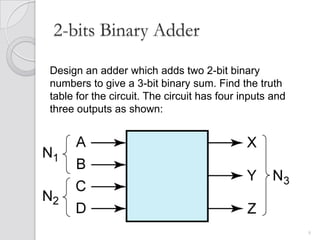
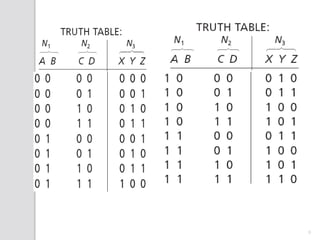
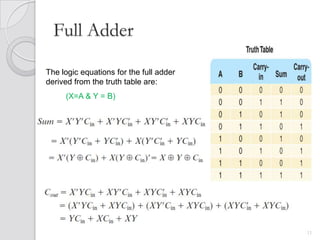
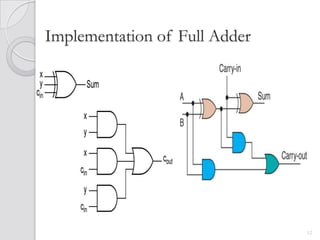
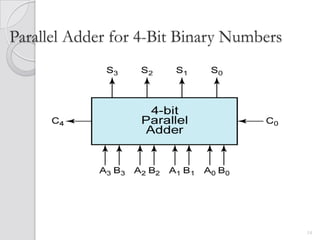
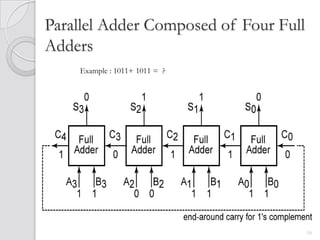
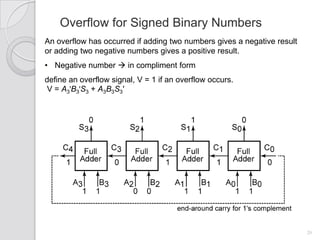
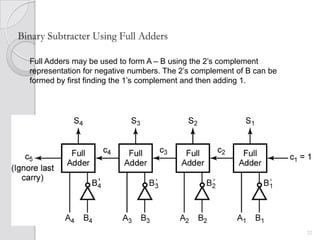
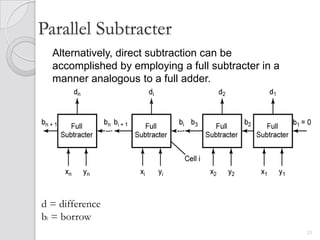
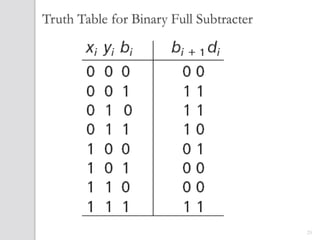
This document discusses digital adders and subtracters. It begins by explaining half adders and full adders, which are used to add binary numbers. It then discusses how to design multi-bit adders using full adders as building blocks. Different approaches for subtraction using full adders and full subtracters are also covered. The document provides circuit diagrams and truth tables to illustrate the designs of basic digital addition and subtraction components.

1. KL 2164
DIGITAL ELECTRONICS
ADDER / SUBSTRACTER
Pn. Wan Nurdiana Wan Ibrahim
nurdiana@eng.ukm.my

2. Contents
Half Adder
Full Adder
Subtracter
2

3. Adder
The result of adding two binary digits could produce a carry value
Recall that 1 + 1 = 10
in base two
Half adder
A circuit that computes the sum of two bits
and produces the correct carry bit
Full Adder
A circuit that takes the carry-in value into account
3

4. Contents
Half Adder
Full Adder
Subtracter
4

5. Example of 1-bit Adder
Design a simple binary adder that adds two 1-bit binary
numbers, a and b, to give a 2-bit sum. The numeric
values for the adder inputs and outputs are as follows:
5

6. Represent inputs to the adder by the logic
variables A and B and the 2-bit sum by the logic
variables X and Y, and the truth table:
Because a numeric value of 0 is represented by a logic
0 and a numeric value of 1 by a logic 1, the 0’s and 1’s
in the truth table are exactly the same as in the previous
table.
Boolean expression :
6

7. Half Adder
 Circuit diagram representing a half adder
 Boolean expressions
sum = A B
carry = AB
7

8. 2-bits Binary Adder
Design an adder which adds two 2-bit binary
numbers to give a 3-bit binary sum. Find the truth
table for the circuit. The circuit has four inputs and
three outputs as shown:
8

9. 9

10. Contents
Half Adder
Full Adder
Subtracter
10

11. Full Adder
The logic equations for the full adder
derived from the truth table are:
(X=A & Y = B)
11

12. Implementation of Full Adder
12

13. Design of Binary Adders and Subtracters
Design a parallel adder that adds two
4-bit unsigned binary numbers and a
carry input to give a 4-bit sum and a
carry output.
13

14. Parallel Adder for 4-Bit Binary Numbers
14

15. One approach would be to construct a truth
table with nine inputs and five outputs and
then derive and simplify the five output
equations.
A better method is to design a logic module
that adds two bits and a carry, and then
connect four of these modules together to
form a 4-bit adder.
15

16. Parallel Adder Composed of Four Full
Adders
Example : 1011+ 1011 = ?
16

17. One’s complement addition
 To add one’s complement numbers:
◦ First do unsigned addition on the numbers, including the sign bits.
◦ Then take the carry out and add it to the sum.
 Two examples:
0111 (+7) 0011 (+3)
+ 1011 + (-4) + 0010 + (+2)
1 0010 0 0101
0010 0101
+ 1 + 0
0011 (+3) 0101 (+5)
 This is simpler and more uniform than signed magnitude
addition.
17

18. Two’s complement addition
 Negating a two’s complement number takes a bit of work, but
addition is much easier than with the other two systems.
 To find A + B, you just have to:
◦ Do unsigned addition on A and B, including their sign bits.
◦ Ignore any carry out.
 For example, to find 0111 + 1100, or (+7) + (-4):
◦ First add 0111 + 1100 as unsigned numbers:
01 1 1
+ 1 1 00
1 001 1
◦ Discard the carry out (1).
◦ The answer is 0011 (+3).
18

19. Unsigned numbers overflow
 Carry-out can be used to detect overflow
 The largest number that we can represent with 4-bits
using unsigned numbers is 15
 Suppose that we are adding 4-bit numbers: 9 (1001) and
10 (1010).
1 001 (9)
+ 1 0 10 (10)
1 001 1 (19)
 The value 19 cannot be represented with 4-bits
 When operating with unsigned numbers, a carry-out of
1 can be used to indicate overflow
19

20. Overflow for Signed Binary Numbers
An overflow has occurred if adding two numbers gives a negative result
or adding two negative numbers gives a positive result.
• Negative number  in compliment form
define an overflow signal, V = 1 if an overflow occurs.
V = A3′B3′S3 + A3B3S3′
20

21. Contents
Half Adder
Full Adder
Subtracter
21

22. Binary Subtracter Using Full Adders
Full Adders may be used to form A – B using the 2’s complement
representation for negative numbers. The 2’s complement of B can be
formed by first finding the 1’s complement and then adding 1.
22

23. Parallel Subtracter
Alternatively, direct subtraction can be
accomplished by employing a full subtracter in a
manner analogous to a full adder.
d = difference
bi = borrow
23

24. Consider xi = 0, yi = 1, and bi = 1:
Step 1 : (if b=1) X= Xi – 1= 0 – 1 Need to borrow from column i+1
 bi+1 =1 & adding 10 (210) to Xi
Step 2 : X = 10 – 1 = 1
Step 3 : X -Y = 1 – 1  d = 0
24

25. Truth Table for Binary Full Subtracter
25