1) The ALU performs arithmetic operations like addition, subtraction, multiplication and division on fixed point and floating point numbers. Fixed point uses integers while floating point uses a sign, mantissa, and exponent. 2) Binary numbers are added using half adders and full adders which are logic circuits that implement addition using truth tables and K-maps. Subtraction is done using 1's or 2's complement representations. 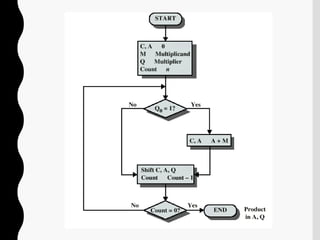3) Multiplication is done using sequential or Booth's algorithm approaches while division uses restoring or non-restoring algorithms. Floating point uses similar addition and subtraction steps but first normalizes the exponents.

1. UNIT II
ARITHMETIC FOR COMPUTERS

2. ALU
• ALU is responsible for performing arithmetic
operations such as addition, subtraction,
multiplication, division and logical operations
such as AND, OR, NOT
• These are performed based on data types.
1.Fixed point number
2.Floating point number

3. • Fixed point number – positive and negative
integers
• Floating point number - contains both integer
part and fractional part

4. • When lower byte addresses are used for the
more significant bytes.
11 22 33 44
MSB LSB
BIG ENDIAN:
B0 B1 B2 B3
44 33 22 11

5. • When lower byte addresses are used the less
significant bytes.
11 22 33 44
MSB LSB
LITTLE ENDIAN:
B0 B1 B2 B3
11 22 33 44

6. FIXED POINT REPRESENTATION
• Unsigned – 6 , 10
• Signed integers – -15, -24
• Note: Change the Leftmost value for negative
value representation.
• Example:
6 = 0000 0110
-4 = ?
-14= ?

7. 1’S COMPLEMENT REPRESENTATION
• Change all zeros to 1’s and 1’s to zero
• Example:
Find 1’s complement of (11010100) 2 .
Solution:
1’s complement of 11010100 is 00101011.

8. 2’S COMPLEMENT REPRESENTATION
• Add 1 to 1’s complement.
• Example:
Find 2’s complement of (11010100)2 .
Solution:
1’s complement of 11010100 is 00101011.
……….

9. ADDITION AND SUBTRACTION
• Rules relating addition and subtraction
4-(-5)=4+5
6+(-5)= 6binary+ (-5binary)
(+A) - (+B) = (+A) + (-B)
(+A) – (-B) = (+A) + (+B)
(-A) – (+B) = (-A) + (-B)
(-A) – (-B) = (-A) + (+B)

10. BINARY ADDITION
0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 1 0
1+1+1=1 1

11. • Example: Add (6)10 with (7) 10 in binary.
Upper significant bit (carry)
1 1 CARRY
0 1 1 0 = (6) 10
0 1 1 1 = (7) 10
1 1 0 1 = (13) 10
Lower significant
bit(sum)

12. HALF ADDER
• A combinational circuit which performs two
bits addition is called Half adder.
• The circuit which performs three bits addition
is called Full adder.

13. HALF ADDER – TRUTH TABLE

14. K-MAP
• A diagram consisting of rectangular array of
squares each represent a different
combination of the variables of a Boolean
function.
Example:

15. CONTD..
K-Map for Carry Logic diagram
for carry
Carry =
AB

16. CONTD..
K-Map for Sum
Input Output
A B
0 0 0
0 1 1
1 0 1
1 1 0
EX-OR:
Logic Diagram:

17. LOGIC DIAGRAM FOR HALF
ADDER:
A
B

18. • The combinational circuit which performs
three bits addition is called Full adder.
• It consist of three inputs(A,B,C in (previous
lower significant) )and two outputs.
FULL ADDER

19. BLOCK SCHEMATIC OF FULL
ADDER

20. TRUTH TABLE

21. K-Map for
Cout
K-Map for Sum:

22. LOGIC DIAGRAM FOR FULL
ADDER:

23. • Rules of binary subtraction are as follows:
0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
0 - 1 = 1 with a borrow of 1
BINARY SUBTRACTION

24. • Example:
Perform (11101100)2 – (00110010)2
1 1 1 0 1 1 0 0
- 0 0 1 1 0 0 1 0
1 0 1 1 1 0 1 0

25. • Rules:
1. Take 1’s complement of B
2. Result = A + (1’s compl. of B)
3. Carry is generated then add it to Result and
mark it as Positive
4. Carry not generated means mark it as
Negative.
BINARY SUBTRACTION FOR 1’S
COMPLEMENT

26. • Example:
Perform (28)10 – (15)10 using 6 bit 1’s
complement representation.

27. • Example:
Perform (28)10 – (15)10 using 6 bit 1’s
complement representation.
(28)10 -011100
(15)10 - 001111
011100
110000 (+)
1001100
1 (+)
001101

28. • Rules:
1. Take 2’s complement of B
2. Result = A + (2’s compl. of B)
3. Carry is generated then add it to Result and
mark it as Positive, ignore the carry.
4. Carry not generated means mark it as
Negative.
BINARY SUBTRACTION FOR 2’S
COMPLEMENT

29. PARALLEL SUBTRACTOR
• 2’s complement is obtained for A – B then 1’s
complement is implemented with inverters to
get 2’s complement.

30. OVERFLOW IN INTEGER
• When both operand A and B have +sign,
when the result comes in –sign then this state
is known as Arithmetic Overflow.
• Eg. Find (7)10 + (3)10 assume 6bit, then get
2’s complement for it.
111 Carry
0111
0011 (+)
1010 Result of 2’s complement is 6.

31. DESIGN OF FAST ADDER
• The sum and carry outputs of any stage
cannot be produced until the input carry
occurs; this leads to a time delay in the
addition process.
0 1 0 1
0 0 1 1 +
1 0 0 0

32. MULTIPLICATION
Sequential Multiplication of Positive
numbers
• Multiplication process involves generation of
partial products, one for each digit in the
multiplier. These partial products are summed
to get final result.

33. SEQUENTIAL MULTIPLICATION
OF POSITIVE NUMBERS

35. SIGN MULTIPLICATION-
BOOTH’S ALGORITHM
• Booth’s algorithm scheme:
(1,1) & (0,0) -> 0
(1,0) -> 1
(0,1) -> -1

36. • Example :
Recode the multiplier 101100 for booth’s
multiplication.
1 0 1 1 0 0 0 implied zero
-1 1 0 -1 0 0

37. • Example :
Multiply 01110 (14) and 11011 (-5).
Sol:
01110 = 14 (multiplicand)
11011 = -5 (multiplier)
01-101 (Recode multiplier)
11011 X 01-101 = 1110111010 (-70)

38. SIGN MULTIPLICATION-BOOTH’S
ALGORITHM

39. BIT PAIR RECODING OF
MULTIPLIERS
• Bit Pair recoding is used to speed up Booth’s
algorithm process.

40. 1. Multiply given 2’s complement no. using bit-
pair recoding A= 110101 multiplicand (-11)
B= 011011 multiplier (+27)
Ans : 111011010111 (-297)
2. Multiply the following pair of signed 2’s
complement numbers using bit-pair recoding of
the multipliers A= 010111 (+23), B= 101100 (-
20).
Ans : 111000110100 (-460)

41. DIVISION
• Division process is similar to the decimal
numbers.
Divisor = 110
Dividend = 11011011
Quotient = 1000100
Remainder = 00011

42. RESTORING DIVISION
ALGORITHM

43. • Perform the division of following no.
using restoring division algorithm:
Dividend = 1010
Divisor = 0011
Divided = 1000, Divisor = 11

45. FLOATING POINT
REPRESENTATION
• To accommodate large values floating point
numbers are used.
• It has three fields:
1111101.1110010
1. 1111011110010 x 25
Mantissa
{ Scaling factor
Exponent
Sign

47. EXCEPTIONS
• Underflow – less than -127
• Overflow – greater than +127
• Divide by Zero
• Inexact – Rounding off
• Invalid – 0/0, input

48. RULES FOR EXPONENT
• If exponent is +ve, to get equal value at both
side increment to the higher value.
Eg:
1.75 X 102 and 6.8 x 104 then change 1.75 x
102 to 0.0175 x 104
• If the decimal value needs to move forward
position of the floating point means then
exponent value need to increased.
Eg. 1.75 X 102 -> 0.0175 x 104

49. • If exponent is -ve, to get equal value at both
side decrement to the lower value.
Eg –
Subtract 1.1 x 2-1 and 1.0001 x 2-2 then change
1.0001 x 2-2 to 0.10001 x 2-1
• If the decimal value needs to move backward
position of the floating point means then
exponent value need to decrease in –ve sign.
Eg. 1.0001 x 2-2 -> 0.10001 x 2-1

50. FLOATING POINT ADDITION
AND SUBTRACTION
Ex: Perform addition and subtraction of single precision
floating point numbers A and B,
A = 44900000H B= 42A00000H
• Step 1: Single precision format
A=
B=
0 1 0 0 0 1 0 0 1 0 0 1 0 0 0 0 0 0 . . . 0 0
sig
n
E’ Mantiss
a
0 1 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0 0 . . . 0 0

51. • Exponent for A = 1000 1001 = 137
• Actual exponent = 137-127 =10
• Exponent for B = 1000 0101= 133
• Actual exponent= 133-127 = 6
Step 2: shifted mantissa of B (4 bits)
B = 0000 01000…..0

52. Step 3 : add mantissas,
A = 0010000….0 , B=0000010…0
Result (A+B)= 00100100…0
A+B=
Step 4: subtract mantissas,
A = 0010000….0 , -B = 1111110000….0
Result (A-B)= 00011100…0
A-B=
0 1 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 . . . 0 0
0 1 0 0 0 1 0 0 1 0 0 0 1 1 1 0 0 0 . . . . 0

53. • Add the numbers (0.75)10 and (-0.275)10 in
binary using the floating point addition algorithm.
Solution:
Step 1:
0.75 x 2= 1.5 -> 1 0.275 x 2 = 0.55 -> 0
0.5 x 2 = 1.0 -> 1 0.55 x 2 = 1.10 -> 1
0.1 x 2 = 0.20 -> 0
0.20 x 2 = 0.40 -> 0
0.40 x 2 = 0.8 -> 0
0.80 x 2 = 1.60 -> 1
0.60 x 2 = 1.20 -> 1
0.20 x 2 = 0.40 -> 0

54. (0.75)10 = (0.11)2 = 1.1 x 2-1
-(0.275)10 = -(0.01000110)2=> -(1.000110 x 2-2)
=> -(0.1000110 x 2-1)
Step 2:
1.1 x 2-1 + -0.1000110 x 2-1= 0.1111010 x 2-1
Step 3:
Normalize the result
1.111010 x 2-2

55. Ex 1 : (0.5) 10 and (0.4375) 10
0.5= 0.1= 1.0 x 2-1
0.4375 = 0.0111=1.110 x 2-2
Multiply (1.0 x 2-1 )X (1.110 x 2-2 ) = 1.110000x
2-3
0.001110000 = 0.21875 10

56. SUBWORD PARALLELISM
• Subword parallelism, multiple subwords are
packed into a word and then process whole
words.
• This is a form of SIMD(Single Instruction
Multiple Data) processing.
• For example if word size is 64bits and
subwords sizes are 8,16 and 32 bits.

57. GUARD BITS AND
TRUNCATION
• Extra bits added to round off calculations is
called as Guard Bits.
• 3 bit value is allowed after rounding off.
• 3 common methods namely:
1. Chopping
2. Von Neumann rounding
3. Rounding

58. 1. CHOPPING
• Simplest method
Eg.
0.00111 to 0.001
Original number 0. b-1 b-2 b-3 b-4 b-5 b-6
Truncated number 0. b-1 b-2 b-3

59. 2.VON NEUMANN METHOD
• If any bits to be removed are 1, then least
significant bit is retained as 1.
• Eg.
0.011000 -> 0.011
0.011010 -> 0.011
0.010010 -> 0.011
Original number 0. b-1 b-2 b-3 b-4 b-5 b-
6
With b-4 b-5 b-6 =000
0. b-1 b-2 b-3 b-4 b-5 b-6
With b-4 b-5 b-6 !=000
Truncated
number
0. b-1 b-2 b-3 0. b-1 b-2 1

60. 3.ROUNDING
• Best method truncation
• Eg.
0.01101 -> 0.011
0.011100 -> (0.011+0.001) -> 0.100
Original number 0. b-1 b-2 b-3 b-4 b-5 b-
6
With b-4 =0
0. b-1 b-2 b-3 b-4 b-5 b-6
With b-4 =1
Truncated
number
0. b-1 b-2 b-3 0. b-1 b-2 b-3 +0.001