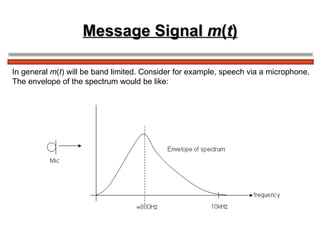
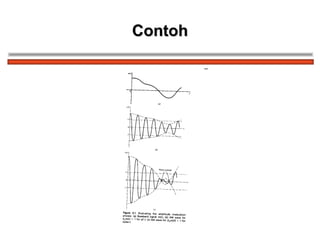
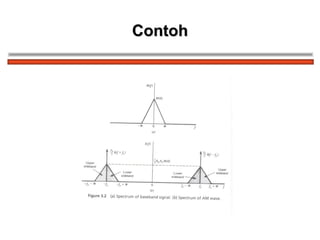
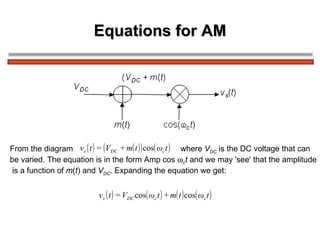
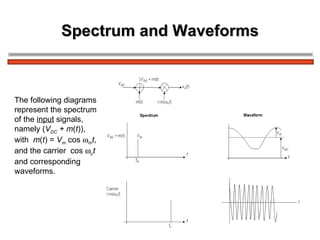
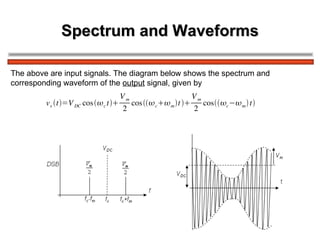
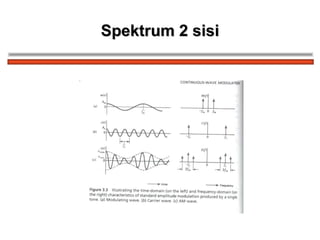
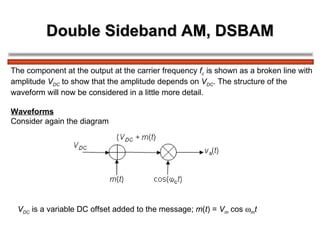
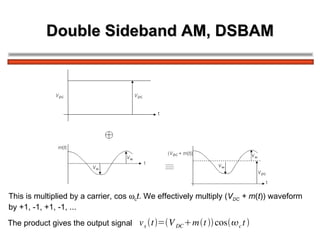
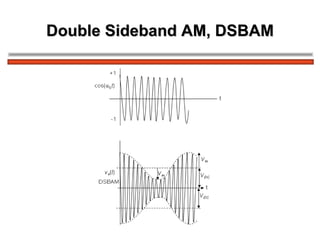
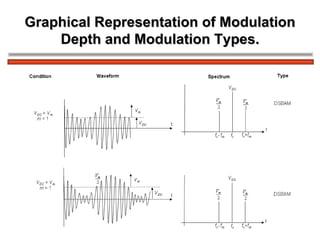
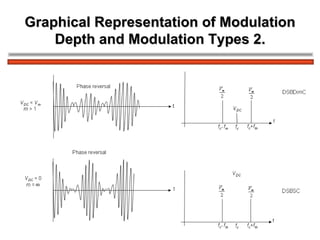
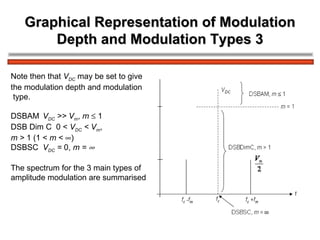
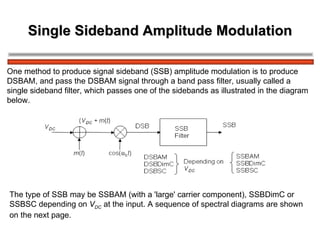
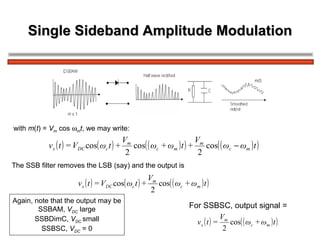
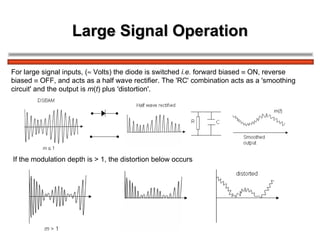
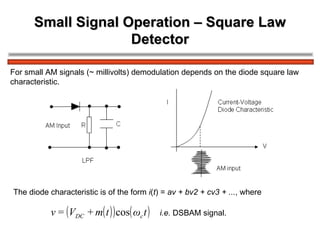
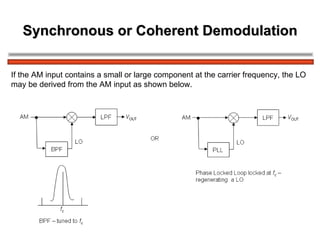
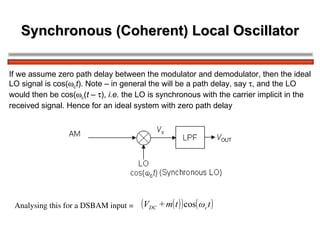
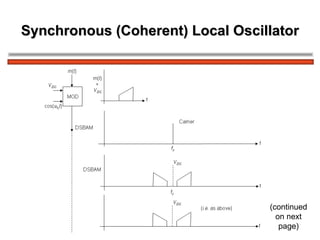
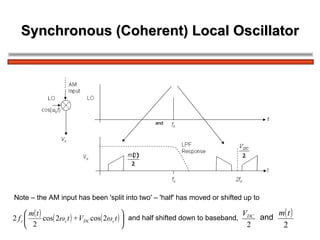
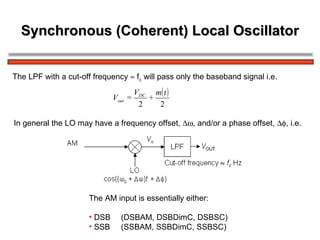
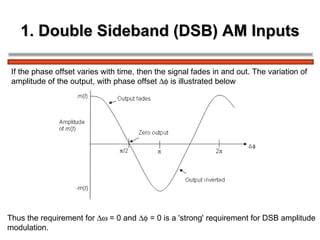
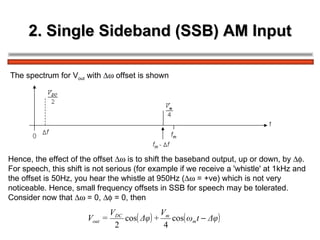
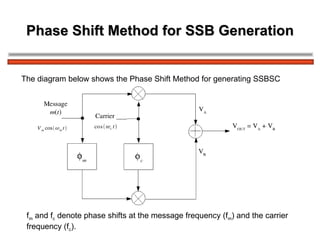
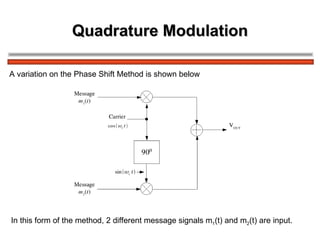
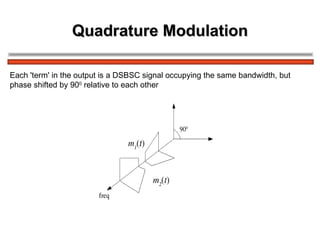
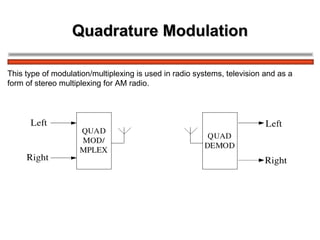
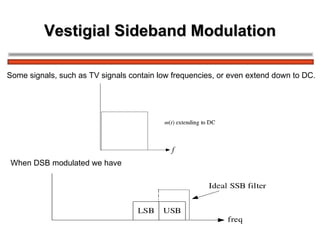
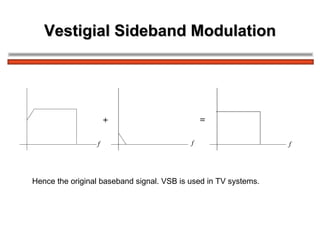
The document discusses amplitude modulation (AM) and different types of AM including double sideband AM (DSBAM), single sideband AM (SSBAM), and their modulation, demodulation, bandwidth requirements, and power considerations. It provides equations, diagrams, and explanations for DSBAM, SSBAM, and synchronous demodulation. Key aspects covered include the carrier signal, message signal, sidebands, modulation depth, spectrum analysis, and transmitter power efficiency comparisons between DSBAM and SSBAM.