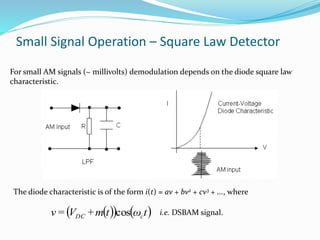
The document discusses double sideband amplitude modulation (DSB AM) and its power considerations. It introduces the standard equation for DSB AM and explains its spectrum components of carrier, upper sideband, and lower sideband. It then discusses the depth of modulation and power efficiency of DSB AM. Specifically, it provides two equivalent equations for calculating the total power of a DSB AM signal and the proportion of "useful" power to total power. Finally, it describes small signal demodulation using a square law detector, showing that the output contains the modulating signal m(t).

1. PRESENTED BY
MS.SHANKHA MITRA SUNANI

2. CONTENT
 Introduction
 Standard equation and its spectrum
 Depth of modulation
 Power consideration in DSBC AM and its
efficiency
 Reconstruction of DSBC AM

3. INTRODUCTION TO DSBC AM
From the diagram
where VDC is the DC voltage that can be varied.. Expanding the equation we get:
      tωtm+V=tv cDCs cos
       tωtm+tωV=tv ccDCs coscos
Now let m(t) = Vm cos mt, i.e. a 'test' signal,        tωtωV+tωV=tv cmmcDCs coscoscos
    BA+B+A=BA coscos
2
1
coscos we have
         tωω
V
+tω+ω
V
+tωV=tv mc
m
mc
m
cDCs cos
2
cos
2
cos

4. Components: Carrier USB LSB
Amplitude: VDC Vm/2 Vm/2
Frequency: c c + m c – m
fc fc + fm fc - fm
Modulation Depth Consider again the equation       tωtωV+V=tv cmmDCs coscos
which may be written as
     tωtω
V
V
+V=tv cm
DC
m
DCs coscos1 





The ratio is
DC
m
V
V defined as the modulation depth, m, i.e.
DC
m
V
V
=m

5. The above are input signals. The diagram below shows the spectrum and
corresponding waveform of the output signal, given by
         tωω
V
+tω+ω
V
+tωV=tv mc
m
mc
m
cDCs cos
2
cos
2
cos
Spectrum and Waveforms

6. From this we may write two equivalent equations for the total power PT, in a DSBAM signal
42882
22222
mDCmmDC
T
V
+
V
=
V
+
V
+
V
=P
The carrier power
2
2
DC
c
V
=P
44
22
m
P+
m
P+P=P cccT 





2
1
2
m
+P=P cT
and
882
22222
DCDCDC
T
Vm
+
Vm
+
V
=P
ori.e.
Either of these forms may be useful. Since both USB and LSB contain the same information a
useful ratio which shows the proportion of 'useful' power to total power is
2
2
2
2
24
2
1
4
m+
m
=
m
+P
m
P
=
P
P
c
c
T
USB






Power Considerations in DSBAM

7. Small Signal Operation – Square Law Detector
For small AM signals (~ millivolts) demodulation depends on the diode square law
characteristic.
The diode characteristic is of the form i(t) = av + bv2 + cv3 + ..., where
    tωtm+V=v cDC cos i.e. DSBAM signal.

8. Small Signal Operation – Square Law Detector
           ...coscos
2
+tωtm+Vb+tωtm+Va cDCcDC
          ...cos2m(t)cos 222
+tωtm+tmV+Vb+tωtCOSaV cDCDCccDC 
          





 tω+tbm+tmbVbV+tωtam+tCOSaV cDCDCcCDC 2cos
2
1
2
1
2cos
22

          ...2cos
222
2
2
coscos
2
22
+tω
V
b+
tbm
+
tmbV
+
bV
+tωtam+taV c
DCDCDC
ccDC 
 tmbV+
bV
DC
2DC
2
=
=
=
'LPF' removes components.
Signal out = i.e. the output contains m(t)
i.e.

9. THANK YOU