Uploaded byalg1testreview
PPTX, PDF210 views

43literal equations

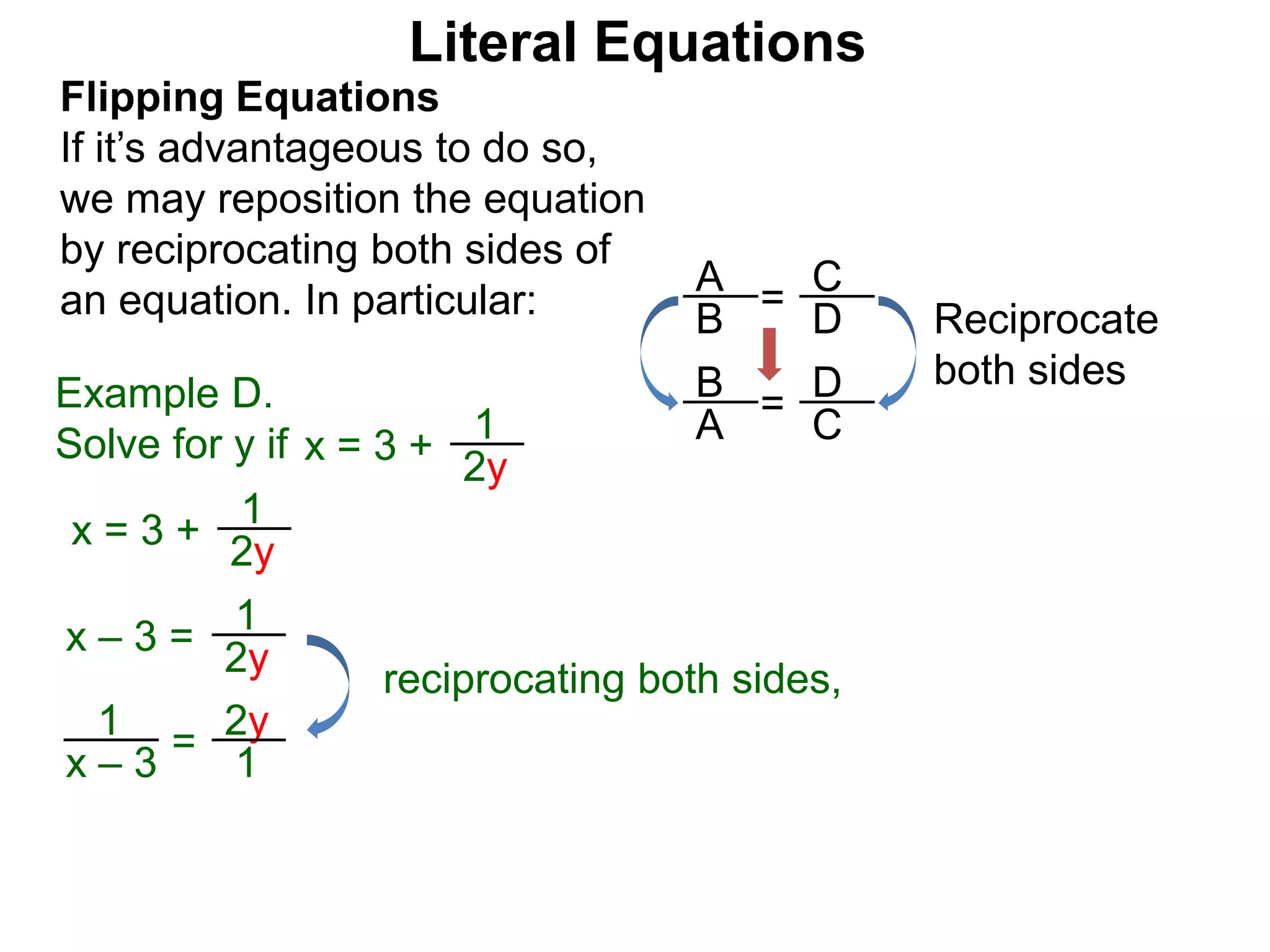
The document discusses solving literal equations by isolating the variable of interest on one side of the equation. It provides examples of solving equations for various variables by adding, subtracting, multiplying, or dividing both sides of the equation by the same quantity. The goal is to isolate the variable being solved for so it stands alone on one side of the equal sign. Steps include clearing fractions, moving all other terms to the other side of the equation, and then dividing both sides by the coefficient of the variable being solved for.

Embed presentation

Download to read offline
Literal Equations
Given an equation with many variables, to solve for a particular variable means to isolate that variable to one side of the equation. Literal Equations
Given an equation with many variables, to solve for a particular variable means to isolate that variable to one side of the equation. Literal Equations Example A. a. Solve for x if x + b = c b. Solve for w if yw = 5.
Given an equation with many variables, to solve for a particular variable means to isolate that variable to one side of the equation. We try to accomplish this just as solving equations for the x, by +, – the same term, or * , / by the same quantity to both sides of the equations. Example A. a. Solve for x if x + b = c Literal Equations b. Solve for w if yw = 5.
Given an equation with many variables, to solve for a particular variable means to isolate that variable to one side of the equation. We try to accomplish this just as solving equations for the x, by +, – the same term, or * , / by the same quantity to both sides of the equations. Example A. a. Solve for x if x + b = c Remove b from the LHS by subtracting from both sides x + b = c –b –b x = c – b Literal Equations b. Solve for w if yw = 5.
Example A. a. Solve for x if x + b = c Remove b from the LHS by subtracting from both sides x + b = c –b –b x = c – b Literal Equations b. Solve for w if yw = 5. Remove y from the LHS by dividing both sides by y. Given an equation with many variables, to solve for a particular variable means to isolate that variable to one side of the equation. We try to accomplish this just as solving equations for the x, by +, – the same term, or * , / by the same quantity to both sides of the equations.
Example A. a. Solve for x if x + b = c Remove b from the LHS by subtracting from both sides x + b = c –b –b x = c – b Literal Equations b. Solve for w if yw = 5. Remove y from the LHS by dividing both sides by y. yw = 5 yw/y = 5/y Given an equation with many variables, to solve for a particular variable means to isolate that variable to one side of the equation. We try to accomplish this just as solving equations for the x, by +, – the same term, or * , / by the same quantity to both sides of the equations.
Example A. a. Solve for x if x + b = c Remove b from the LHS by subtracting from both sides x + b = c –b –b x = c – b 5 y Literal Equations b. Solve for w if yw = 5. Remove y from the LHS by dividing both sides by y. yw = 5 yw/y = 5/y w = Given an equation with many variables, to solve for a particular variable means to isolate that variable to one side of the equation. We try to accomplish this just as solving equations for the x, by +, – the same term, or * , / by the same quantity to both sides of the equations.
Literal Equations Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
To solve for a specific variable in a simple literal equation, do the following steps. Literal Equations Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
To solve for a specific variable in a simple literal equation, do the following steps. 1. If there are fractions in the equations, multiple by the LCD to clear the fractions. Literal Equations Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
To solve for a specific variable in a simple literal equation, do the following steps. 1. If there are fractions in the equations, multiple by the LCD to clear the fractions. 2. Isolate the term containing the variable we wanted to solve for Literal Equations Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
To solve for a specific variable in a simple literal equation, do the following steps. 1. If there are fractions in the equations, multiple by the LCD to clear the fractions. 2. Isolate the term containing the variable we wanted to solve for – move all the other terms to other side of the equation. Literal Equations Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
To solve for a specific variable in a simple literal equation, do the following steps. 1. If there are fractions in the equations, multiple by the LCD to clear the fractions. 2. Isolate the term containing the variable we wanted to solve for – move all the other terms to other side of the equation. 3. Isolate the specific variable by dividing the rest of the factor to the other side. Literal Equations Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
To solve for a specific variable in a simple literal equation, do the following steps. 1. If there are fractions in the equations, multiple by the LCD to clear the fractions. 2. Isolate the term containing the variable we wanted to solve for – move all the other terms to other side of the equation. 3. Isolate the specific variable by dividing the rest of the factor to the other side. Literal Equations Example B. a. Solve for x if (a + b)x = c Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
To solve for a specific variable in a simple literal equation, do the following steps. 1. If there are fractions in the equations, multiple by the LCD to clear the fractions. 2. Isolate the term containing the variable we wanted to solve for – move all the other terms to other side of the equation. 3. Isolate the specific variable by dividing the rest of the factor to the other side. Literal Equations Example B. a. Solve for x if (a + b)x = c (a + b) x = c div the RHS by (a + b) Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
To solve for a specific variable in a simple literal equation, do the following steps. 1. If there are fractions in the equations, multiple by the LCD to clear the fractions. 2. Isolate the term containing the variable we wanted to solve for – move all the other terms to other side of the equation. 3. Isolate the specific variable by dividing the rest of the factor to the other side. Literal Equations Example B. a. Solve for x if (a + b)x = c (a + b) x = c x = c (a + b) div the RHS by (a + b) Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
b. Solve for w if 3y2w = t – 3 Literal Equations
b. Solve for w if 3y2w = t – 3 3y2w = t – 3 div the RHS by 3y2 Literal Equations
b. Solve for w if 3y2w = t – 3 3y2w = t – 3 w = t – 3 3y2 div the RHS by 3y2 Literal Equations
b. Solve for w if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 w = t – 3 3y2 div the RHS by 3y2 Literal Equations
b. Solve for w if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 w = t – 3 3y2 div the RHS by 3y2 move b2 to the RHS Literal Equations
b. Solve for w if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 div the RHS by 3y2 move b2 to the RHS Literal Equations
b. Solve for w if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations
b. Solve for w if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations
b. Solve for w if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations d. Solve for y if a(x – y) = 10
b. Solve for w if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations d. Solve for y if a(x – y) = 10 a(x – y) = 10 expand
b. Solve for w if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations d. Solve for y if a(x – y) = 10 a(x – y) = 10 expand ax – ay = 10
b. Solve for w if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations d. Solve for y if a(x – y) = 10 a(x – y) = 10 expand ax – ay = 10 subtract ax
b. Solve for w if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations d. Solve for y if a(x – y) = 10 a(x – y) = 10 expand ax – ay = 10 subtract ax – ay = 10 – ax
b. Solve for w if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations d. Solve for y if a(x – y) = 10 a(x – y) = 10 expand ax – ay = 10 subtract ax – ay = 10 – ax div by –a
b. Solve for w if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations d. Solve for y if a(x – y) = 10 a(x – y) = 10 expand ax – ay = 10 subtract ax – ay = 10 – ax div by –a y = 10 – ax –a
Multiply by the LCD to get rid of the denominator then solve. Literal Equations
–4 = d 3d + b Multiply by the LCD to get rid of the denominator then solve. Example C. Solve for d if Literal Equations
–4 = d 3d + b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d– 4 = d 3d + b Example C. Solve for d if Literal Equations
–4 = d 3d + b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d d – 4 = d 3d + b – 4 = d 3d + b ( ) d Example C. Solve for d if Literal Equations
–4 = d 3d + b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d d – 4 = d 3d + b – 4 = d 3d + b ( ) d Example C. Solve for d if Literal Equations
–4 = d 3d + b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d d – 4 = d 3d + b – 4 = d 3d + b ( ) d – 4d = 3d + b Example C. Solve for d if Literal Equations
–4 = d 3d + b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d d – 4 = d 3d + b – 4 = d 3d + b ( ) d – 4d = 3d + b move –4d and b Example C. Solve for d if Literal Equations
–4 = d 3d + b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d d – 4 = d 3d + b – 4 = d 3d + b ( ) d – 4d = 3d + b – b = 3d + 4d move –4d and b Example C. Solve for d if Literal Equations
–4 = d 3d + b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d d – 4 = d 3d + b – 4 = d 3d + b ( ) d – 4d = 3d + b – b = 3d + 4d move –4d and b – b = 7d Example C. Solve for d if Literal Equations
–4 = d 3d + b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d d – 4 = d 3d + b – 4 = d 3d + b ( ) d – 4d = 3d + b – b = 3d + 4d move –4d and b – b = 7d = d 7 –b Example C. Solve for d if Literal Equations div. by 7
Flipping Equations If it’s advantageous to do so, we may reposition the equation by reciprocating both sides of an equation. Literal Equations x = 3 + 1 2y Example D. Solve for y if
Flipping Equations Literal Equations
Flipping Equations Literal Equations x = 3 + 1 2y Example D. Solve for y if
Flipping Equations If it’s advantageous to do so, we may reposition the equation by reciprocating both sides of an equation. Literal Equations x = 3 + 1 2y Example D. Solve for y if
= D C Flipping Equations If it’s advantageous to do so, we may reposition the equation by reciprocating both sides of an equation. In particular: Literal Equations B A = C D A B Reciprocate both sides x = 3 + 1 2y Example D. Solve for y if
= D C Flipping Equations If it’s advantageous to do so, we may reposition the equation by reciprocating both sides of an equation. In particular: x = 3 + 1 2y Example D. Solve for y if Literal Equations B A = C D A B x = 3 + 1 2y Reciprocate both sides
= D C Flipping Equations If it’s advantageous to do so, we may reposition the equation by reciprocating both sides of an equation. In particular: x = 3 + 1 2y Example D. Solve for y if Literal Equations B A = C D A B x = 3 + 1 2y x – 3 = 1 2y Reciprocate both sides
= D C Flipping Equations If it’s advantageous to do so, we may reposition the equation by reciprocating both sides of an equation. In particular: x = 3 + 1 2y Example D. Solve for y if Literal Equations B A = C D A B x = 3 + 1 2y x – 3 = 1 2y reciprocating both sides, = 1 2y x – 3 1 Reciprocate both sides
= D C Flipping Equations If it’s advantageous to do so, we may reposition the equation by reciprocating both sides of an equation. In particular: x = 3 + 1 2y Example D. Solve for y if Literal Equations B A = C D A B x = 3 + 1 2y x – 3 = 1 2y reciprocating both sides, then div. by 2 = 1 2y x – 3 1 = 2y 2(x – 3) 1 Reciprocate both sides 2
= D C Flipping Equations If it’s advantageous to do so, we may reposition the equation by reciprocating both sides of an equation. In particular: x = 3 + 1 2y Example D. Solve for y if Literal Equations B A = C D A B x = 3 + 1 2y x – 3 = 1 2y reciprocating both sides, then div. by 2 = 1 2y x – 3 1 = 2y 2(x – 3) 1 Reciprocate both sides 2 = y or 2(x – 3) 1 y =
Exercise. Solve for the indicated variables. Literal Equations 1. a – b = d – e for b. 2. a – b = d – e for e. 3. 2*b + d = e for b. 4. a*b + d = e for b. 5. (2 + a)*b + d = e for b. 6. 2L + 2W = P for W 7. (3x + 6)y = 5 for y 8. 3x + 6y = 5 for y w = t – 3 613. for t w = t – b a14. for t w =11. for t w =12. for t t 6 6 t w = 3t – b a15. for t 16. (3x + 6)y = 5 for x w = t – 3 6 17. + a for t w = at – b 5 18. for t w = at – b c 19. + d for t 3 = 4t – b t 20. for t 9. 3x + 6xy = 5 for y 10. 3x – (x + 6)y = 5z for y

More Related Content

PPTX
1 4 cancellation
bymath123b
 
PPTX
4.5 calculation with log and exp
bymath260
 
PPTX
1.1 review on algebra 1
bymath265
 
PPT
1.4 review on log exp-functions
bymath265
 
PPTX
5 7applications of factoring
bymath123a
 
PPTX
1.3 solving equations
bymath260
 
PPTX
44 exponents
byalg1testreview
 
PPTX
47 operations of 2nd degree expressions and formulas
byalg1testreview
 
1 4 cancellation
bymath123b
 
4.5 calculation with log and exp
bymath260
 
1.1 review on algebra 1
bymath265
 
1.4 review on log exp-functions
bymath265
 
5 7applications of factoring
bymath123a
 
1.3 solving equations
bymath260
 
44 exponents
byalg1testreview
 
47 operations of 2nd degree expressions and formulas
byalg1testreview
 

What's hot

PPT
2.5 calculation with log and exp
bymath123c
 
PPT
3.2 more on log and exponential equations
bymath123c
 
PPTX
2.2 Graphs of First Degree Functions
bymath260
 
PPTX
5 6 substitution and factoring formulas
bymath123a
 
PPTX
46polynomial expressions
byalg1testreview
 
PPTX
1.2 algebraic expressions
bymath260
 
PPT
1.3 sign charts and inequalities
bymath123c
 
PPTX
4 5 fractional exponents
bymath123b
 
PPTX
3 algebraic expressions y
bymath266
 
PPT
1.5 notation and algebra of functions
bymath123c
 
PPTX
3.1 higher derivatives
bymath265
 
PPTX
53 multiplication and division of rational expressions
byalg1testreview
 
PPTX
5 4 equations that may be reduced to quadratics
bymath123b
 
PPTX
4 4 more on algebra of radicals
bymath123b
 
PPTX
27 calculation with log and exp x
bymath260
 
PPTX
55 inequalities and comparative statements
byalg1testreview
 
PPTX
1.2 review on algebra 2-sign charts and inequalities
bymath265
 
PPTX
4 6multiplication formulas
bymath123a
 
PPTX
1exponents
bymath123a
 
PPTX
4 1exponents
bymath123a
 
2.5 calculation with log and exp
bymath123c
 
3.2 more on log and exponential equations
bymath123c
 
2.2 Graphs of First Degree Functions
bymath260
 
5 6 substitution and factoring formulas
bymath123a
 
46polynomial expressions
byalg1testreview
 
1.2 algebraic expressions
bymath260
 
1.3 sign charts and inequalities
bymath123c
 
4 5 fractional exponents
bymath123b
 
3 algebraic expressions y
bymath266
 
1.5 notation and algebra of functions
bymath123c
 
3.1 higher derivatives
bymath265
 
53 multiplication and division of rational expressions
byalg1testreview
 
5 4 equations that may be reduced to quadratics
bymath123b
 
4 4 more on algebra of radicals
bymath123b
 
27 calculation with log and exp x
bymath260
 
55 inequalities and comparative statements
byalg1testreview
 
1.2 review on algebra 2-sign charts and inequalities
bymath265
 
4 6multiplication formulas
bymath123a
 
1exponents
bymath123a
 
4 1exponents
bymath123a
 

Similar to 43literal equations

PPTX
2 5literal equations
bymath123a
 
PPT
Equations Revision
byandrewhickson
 
PPS
Solving Literal Equations
byClayton Rainsberg
 
PPT
Equations Revision
byandrewhickson
 
PPTX
Math Algebra
byMark Brahier
 
PPTX
Consistency of linear equations in two and three variables
byAamlan Saswat Mishra
 
PPTX
Chapter 3. linear equation and linear equalities in one variables
bymonomath
 
PPTX
01 Linear Equations in One Variable.pptx
bymaycanellada
 
PDF
1.1 Linear and Literal Equations
bysmiller5
 
PPT
03.-Equations-and-inequalities-Grade-10-Term-3.ppt
byAmoveemsiza
 
PPTX
basic algebra
byfebe estamo
 
PPTX
Simultaneous equations
byfisayo omoniyi
 
PPTX
5literal equations x
byTzenma
 
PPTX
3linear equations ii x
byTzenma
 
PPT
.
byleoscotch
 
PPTX
Module 6 review
byjjmosley
 
PPTX
Algebra solving no animations
byniamhriordan
 
PDF
Day 12 variables on both sides fractions
byErik Tjersland
 
PDF
Day 12 variables on both sides fractions
byErik Tjersland
 
PDF
Day 9 combining like terms
byErik Tjersland
 
2 5literal equations
bymath123a
 
Equations Revision
byandrewhickson
 
Solving Literal Equations
byClayton Rainsberg
 
Equations Revision
byandrewhickson
 
Math Algebra
byMark Brahier
 
Consistency of linear equations in two and three variables
byAamlan Saswat Mishra
 
Chapter 3. linear equation and linear equalities in one variables
bymonomath
 
01 Linear Equations in One Variable.pptx
bymaycanellada
 
1.1 Linear and Literal Equations
bysmiller5
 
03.-Equations-and-inequalities-Grade-10-Term-3.ppt
byAmoveemsiza
 
basic algebra
byfebe estamo
 
Simultaneous equations
byfisayo omoniyi
 
5literal equations x
byTzenma
 
3linear equations ii x
byTzenma
 
.
byleoscotch
 
Module 6 review
byjjmosley
 
Algebra solving no animations
byniamhriordan
 
Day 12 variables on both sides fractions
byErik Tjersland
 
Day 12 variables on both sides fractions
byErik Tjersland
 
Day 9 combining like terms
byErik Tjersland
 

More from alg1testreview

PPTX
42 linear equations
byalg1testreview
 
PPTX
55 addition and subtraction of rational expressions
byalg1testreview
 
PPTX
57 graphing lines from linear equations
byalg1testreview
 
PPTX
49 factoring trinomials the ac method and making lists
byalg1testreview
 
PPTX
59 constructing linea equations of lines
byalg1testreview
 
PPTX
56 system of linear equations
byalg1testreview
 
PPTX
51 ratio-proportion
byalg1testreview
 
PPTX
51 basic shapes and formulas
byalg1testreview
 
PPTX
54 the number line
byalg1testreview
 
PPTX
54 the least common multiple
byalg1testreview
 
PPTX
33 percentages
byalg1testreview
 
PPTX
45scientific notation
byalg1testreview
 
PPTX
52 about triangles
byalg1testreview
 
PPTX
52 rational expressions
byalg1testreview
 
PPTX
58 slopes of lines
byalg1testreview
 
PPTX
41 expressions
byalg1testreview
 
PPTX
56 the rectangular coordinate system
byalg1testreview
 
PPTX
50 solving equations by factoring
byalg1testreview
 
PPTX
48 factoring out the gcf and the grouping method
byalg1testreview
 
PPTX
53 pythagorean theorem and square roots
byalg1testreview
 
42 linear equations
byalg1testreview
 
55 addition and subtraction of rational expressions
byalg1testreview
 
57 graphing lines from linear equations
byalg1testreview
 
49 factoring trinomials the ac method and making lists
byalg1testreview
 
59 constructing linea equations of lines
byalg1testreview
 
56 system of linear equations
byalg1testreview
 
51 ratio-proportion
byalg1testreview
 
51 basic shapes and formulas
byalg1testreview
 
54 the number line
byalg1testreview
 
54 the least common multiple
byalg1testreview
 
33 percentages
byalg1testreview
 
45scientific notation
byalg1testreview
 
52 about triangles
byalg1testreview
 
52 rational expressions
byalg1testreview
 
58 slopes of lines
byalg1testreview
 
41 expressions
byalg1testreview
 
56 the rectangular coordinate system
byalg1testreview
 
50 solving equations by factoring
byalg1testreview
 
48 factoring out the gcf and the grouping method
byalg1testreview
 
53 pythagorean theorem and square roots
byalg1testreview
 

Recently uploaded

PDF
FAMILY ASSESSMENT FORMAT - CHN practical
byDr. Sudhadevi Sadanandan
 
DOCX
Mobile applications Devlopment ReTest year 2025-2026
byDr. Mazin Mohamed alkathiri
 
PPTX
The Art Pastor's Guide to the Liturgical Calendar
bySteve Thomason
 
PDF
UKSG Forum 2025 - They asked for everything - The Case of the Systematic Revi...
byUKSG: connecting the knowledge community
 
PPTX
CHAPTER NO.08 HCP BY GG CLINICAL PHARMACY
byGanu Gavade
 
PDF
The Pity of War: Form, Fragment, and the Artificial Echo | Understanding War ...
byNidhi Pandya
 
PPTX
ELEMENTS OF COMMUNICATION (UNIT 2) .pptx
byPOOJA KARVANDE
 
PDF
Models of Teaching - TNTEU - B.Ed I Semester - Teaching and Learning - BD1TL ...
byDr Raja Mohammed T
 
PPTX
Vitamins and mineral deficiency , signs and symptoms associated with exercise
byvirupa chandrika reddy
 
PPTX
Limpitlaw "Licensing: From Mindset to Milestones"
byNational Information Standards Organization (NISO)
 
PPTX
TAMIS & TEMS - HOW, WHY and THE STEPS IN PROCTOLOGY
byJohn Thanakumar
 
PDF
Projecte de la porta de primer B: L'antic Egipte
byeduardrubio1
 
PPTX
10-12-2025 Francois Staring How can Researchers and Initial Teacher Educators...
byEduSkills OECD
 
PPTX
How to Manage Reception Report in Odoo 18 Inventory
byCeline George
 
PDF
Current Electricity for first year physiotherapy
byGanesh Jadhav
 
PPTX
How to Manage Line Discounts in Odoo 18 POS
byCeline George
 
PDF
APM Wessex Network: DEIB Policy into Practice
byAssociation for Project Management
 
PDF
All Students Workshop 25 Yoga Wellness by LDMMIA
by©LDMMIA, ©Reiki Yoga
 
PPTX
Pain. definition, causes, factor influencing pain & pain assessment.pptx
byPompi Begum
 
PPTX
Unit I — Introduction to Anatomical Terms and Organization of the Human Body
byRAKESH SAJJAN
 
FAMILY ASSESSMENT FORMAT - CHN practical
byDr. Sudhadevi Sadanandan
 
Mobile applications Devlopment ReTest year 2025-2026
byDr. Mazin Mohamed alkathiri
 
The Art Pastor's Guide to the Liturgical Calendar
bySteve Thomason
 
UKSG Forum 2025 - They asked for everything - The Case of the Systematic Revi...
byUKSG: connecting the knowledge community
 
CHAPTER NO.08 HCP BY GG CLINICAL PHARMACY
byGanu Gavade
 
The Pity of War: Form, Fragment, and the Artificial Echo | Understanding War ...
byNidhi Pandya
 
ELEMENTS OF COMMUNICATION (UNIT 2) .pptx
byPOOJA KARVANDE
 
Models of Teaching - TNTEU - B.Ed I Semester - Teaching and Learning - BD1TL ...
byDr Raja Mohammed T
 
Vitamins and mineral deficiency , signs and symptoms associated with exercise
byvirupa chandrika reddy
 
Limpitlaw "Licensing: From Mindset to Milestones"
byNational Information Standards Organization (NISO)
 
TAMIS & TEMS - HOW, WHY and THE STEPS IN PROCTOLOGY
byJohn Thanakumar
 
Projecte de la porta de primer B: L'antic Egipte
byeduardrubio1
 
10-12-2025 Francois Staring How can Researchers and Initial Teacher Educators...
byEduSkills OECD
 
How to Manage Reception Report in Odoo 18 Inventory
byCeline George
 
Current Electricity for first year physiotherapy
byGanesh Jadhav
 
How to Manage Line Discounts in Odoo 18 POS
byCeline George
 
APM Wessex Network: DEIB Policy into Practice
byAssociation for Project Management
 
All Students Workshop 25 Yoga Wellness by LDMMIA
by©LDMMIA, ©Reiki Yoga
 
Pain. definition, causes, factor influencing pain & pain assessment.pptx
byPompi Begum
 
Unit I — Introduction to Anatomical Terms and Organization of the Human Body
byRAKESH SAJJAN
 

43literal equations

  • 1.
  • 2.
    Given an equationwith many variables, to solve for a particular variable means to isolate that variable to one side of the equation. Literal Equations
  • 3.
    Given an equationwith many variables, to solve for a particular variable means to isolate that variable to one side of the equation. Literal Equations Example A. a. Solve for x if x + b = c b. Solve for w if yw = 5.
  • 4.
    Given an equationwith many variables, to solve for a particular variable means to isolate that variable to one side of the equation. We try to accomplish this just as solving equations for the x, by +, – the same term, or * , / by the same quantity to both sides of the equations. Example A. a. Solve for x if x + b = c Literal Equations b. Solve for w if yw = 5.
  • 5.
    Given an equationwith many variables, to solve for a particular variable means to isolate that variable to one side of the equation. We try to accomplish this just as solving equations for the x, by +, – the same term, or * , / by the same quantity to both sides of the equations. Example A. a. Solve for x if x + b = c Remove b from the LHS by subtracting from both sides x + b = c –b –b x = c – b Literal Equations b. Solve for w if yw = 5.
  • 6.
    Example A. a. Solvefor x if x + b = c Remove b from the LHS by subtracting from both sides x + b = c –b –b x = c – b Literal Equations b. Solve for w if yw = 5. Remove y from the LHS by dividing both sides by y. Given an equation with many variables, to solve for a particular variable means to isolate that variable to one side of the equation. We try to accomplish this just as solving equations for the x, by +, – the same term, or * , / by the same quantity to both sides of the equations.
  • 7.
    Example A. a. Solvefor x if x + b = c Remove b from the LHS by subtracting from both sides x + b = c –b –b x = c – b Literal Equations b. Solve for w if yw = 5. Remove y from the LHS by dividing both sides by y. yw = 5 yw/y = 5/y Given an equation with many variables, to solve for a particular variable means to isolate that variable to one side of the equation. We try to accomplish this just as solving equations for the x, by +, – the same term, or * , / by the same quantity to both sides of the equations.
  • 8.
    Example A. a. Solvefor x if x + b = c Remove b from the LHS by subtracting from both sides x + b = c –b –b x = c – b 5 y Literal Equations b. Solve for w if yw = 5. Remove y from the LHS by dividing both sides by y. yw = 5 yw/y = 5/y w = Given an equation with many variables, to solve for a particular variable means to isolate that variable to one side of the equation. We try to accomplish this just as solving equations for the x, by +, – the same term, or * , / by the same quantity to both sides of the equations.
  • 9.
    Literal Equations Adding orsubtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
  • 10.
    To solve fora specific variable in a simple literal equation, do the following steps. Literal Equations Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
  • 11.
    To solve fora specific variable in a simple literal equation, do the following steps. 1. If there are fractions in the equations, multiple by the LCD to clear the fractions. Literal Equations Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
  • 12.
    To solve fora specific variable in a simple literal equation, do the following steps. 1. If there are fractions in the equations, multiple by the LCD to clear the fractions. 2. Isolate the term containing the variable we wanted to solve for Literal Equations Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
  • 13.
    To solve fora specific variable in a simple literal equation, do the following steps. 1. If there are fractions in the equations, multiple by the LCD to clear the fractions. 2. Isolate the term containing the variable we wanted to solve for – move all the other terms to other side of the equation. Literal Equations Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
  • 14.
    To solve fora specific variable in a simple literal equation, do the following steps. 1. If there are fractions in the equations, multiple by the LCD to clear the fractions. 2. Isolate the term containing the variable we wanted to solve for – move all the other terms to other side of the equation. 3. Isolate the specific variable by dividing the rest of the factor to the other side. Literal Equations Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
  • 15.
    To solve fora specific variable in a simple literal equation, do the following steps. 1. If there are fractions in the equations, multiple by the LCD to clear the fractions. 2. Isolate the term containing the variable we wanted to solve for – move all the other terms to other side of the equation. 3. Isolate the specific variable by dividing the rest of the factor to the other side. Literal Equations Example B. a. Solve for x if (a + b)x = c Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
  • 16.
    To solve fora specific variable in a simple literal equation, do the following steps. 1. If there are fractions in the equations, multiple by the LCD to clear the fractions. 2. Isolate the term containing the variable we wanted to solve for – move all the other terms to other side of the equation. 3. Isolate the specific variable by dividing the rest of the factor to the other side. Literal Equations Example B. a. Solve for x if (a + b)x = c (a + b) x = c div the RHS by (a + b) Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
  • 17.
    To solve fora specific variable in a simple literal equation, do the following steps. 1. If there are fractions in the equations, multiple by the LCD to clear the fractions. 2. Isolate the term containing the variable we wanted to solve for – move all the other terms to other side of the equation. 3. Isolate the specific variable by dividing the rest of the factor to the other side. Literal Equations Example B. a. Solve for x if (a + b)x = c (a + b) x = c x = c (a + b) div the RHS by (a + b) Adding or subtracting a term to both sides may be viewed as moving the term across the " = " and change its sign.
  • 18.
    b. Solve forw if 3y2w = t – 3 Literal Equations
  • 19.
    b. Solve forw if 3y2w = t – 3 3y2w = t – 3 div the RHS by 3y2 Literal Equations
  • 20.
    b. Solve forw if 3y2w = t – 3 3y2w = t – 3 w = t – 3 3y2 div the RHS by 3y2 Literal Equations
  • 21.
    b. Solve forw if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 w = t – 3 3y2 div the RHS by 3y2 Literal Equations
  • 22.
    b. Solve forw if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 w = t – 3 3y2 div the RHS by 3y2 move b2 to the RHS Literal Equations
  • 23.
    b. Solve forw if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 div the RHS by 3y2 move b2 to the RHS Literal Equations
  • 24.
    b. Solve forw if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations
  • 25.
    b. Solve forw if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations
  • 26.
    b. Solve forw if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations d. Solve for y if a(x – y) = 10
  • 27.
    b. Solve forw if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations d. Solve for y if a(x – y) = 10 a(x – y) = 10 expand
  • 28.
    b. Solve forw if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations d. Solve for y if a(x – y) = 10 a(x – y) = 10 expand ax – ay = 10
  • 29.
    b. Solve forw if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations d. Solve for y if a(x – y) = 10 a(x – y) = 10 expand ax – ay = 10 subtract ax
  • 30.
    b. Solve forw if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations d. Solve for y if a(x – y) = 10 a(x – y) = 10 expand ax – ay = 10 subtract ax – ay = 10 – ax
  • 31.
    b. Solve forw if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations d. Solve for y if a(x – y) = 10 a(x – y) = 10 expand ax – ay = 10 subtract ax – ay = 10 – ax div by –a
  • 32.
    b. Solve forw if 3y2w = t – 3 3y2w = t – 3 c. Solve for a if b2 – 4ac = 5 b2 – 4ac = 5 – 4ca = 5 – b2 w = t – 3 3y2 a = 5 – b2 –4c div the RHS by 3y2 move b2 to the RHS div the RHS by –4c Literal Equations d. Solve for y if a(x – y) = 10 a(x – y) = 10 expand ax – ay = 10 subtract ax – ay = 10 – ax div by –a y = 10 – ax –a
  • 33.
    Multiply by theLCD to get rid of the denominator then solve. Literal Equations
  • 34.
    –4 = d 3d +b Multiply by the LCD to get rid of the denominator then solve. Example C. Solve for d if Literal Equations
  • 35.
    –4 = d 3d +b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d– 4 = d 3d + b Example C. Solve for d if Literal Equations
  • 36.
    –4 = d 3d +b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d d – 4 = d 3d + b – 4 = d 3d + b ( ) d Example C. Solve for d if Literal Equations
  • 37.
    –4 = d 3d +b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d d – 4 = d 3d + b – 4 = d 3d + b ( ) d Example C. Solve for d if Literal Equations
  • 38.
    –4 = d 3d +b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d d – 4 = d 3d + b – 4 = d 3d + b ( ) d – 4d = 3d + b Example C. Solve for d if Literal Equations
  • 39.
    –4 = d 3d +b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d d – 4 = d 3d + b – 4 = d 3d + b ( ) d – 4d = 3d + b move –4d and b Example C. Solve for d if Literal Equations
  • 40.
    –4 = d 3d +b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d d – 4 = d 3d + b – 4 = d 3d + b ( ) d – 4d = 3d + b – b = 3d + 4d move –4d and b Example C. Solve for d if Literal Equations
  • 41.
    –4 = d 3d +b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d d – 4 = d 3d + b – 4 = d 3d + b ( ) d – 4d = 3d + b – b = 3d + 4d move –4d and b – b = 7d Example C. Solve for d if Literal Equations
  • 42.
    –4 = d 3d +b Multiply by the LCD to get rid of the denominator then solve. multiply by the LCD d d – 4 = d 3d + b – 4 = d 3d + b ( ) d – 4d = 3d + b – b = 3d + 4d move –4d and b – b = 7d = d 7 –b Example C. Solve for d if Literal Equations div. by 7
  • 43.
    Flipping Equations If it’sadvantageous to do so, we may reposition the equation by reciprocating both sides of an equation. Literal Equations x = 3 + 1 2y Example D. Solve for y if
  • 44.
  • 45.
    Flipping Equations Literal Equations x= 3 + 1 2y Example D. Solve for y if
  • 46.
    Flipping Equations If it’sadvantageous to do so, we may reposition the equation by reciprocating both sides of an equation. Literal Equations x = 3 + 1 2y Example D. Solve for y if
  • 47.
    = D C Flipping Equations If it’sadvantageous to do so, we may reposition the equation by reciprocating both sides of an equation. In particular: Literal Equations B A = C D A B Reciprocate both sides x = 3 + 1 2y Example D. Solve for y if
  • 48.
    = D C Flipping Equations If it’sadvantageous to do so, we may reposition the equation by reciprocating both sides of an equation. In particular: x = 3 + 1 2y Example D. Solve for y if Literal Equations B A = C D A B x = 3 + 1 2y Reciprocate both sides
  • 49.
    = D C Flipping Equations If it’sadvantageous to do so, we may reposition the equation by reciprocating both sides of an equation. In particular: x = 3 + 1 2y Example D. Solve for y if Literal Equations B A = C D A B x = 3 + 1 2y x – 3 = 1 2y Reciprocate both sides
  • 50.
    = D C Flipping Equations If it’sadvantageous to do so, we may reposition the equation by reciprocating both sides of an equation. In particular: x = 3 + 1 2y Example D. Solve for y if Literal Equations B A = C D A B x = 3 + 1 2y x – 3 = 1 2y reciprocating both sides, = 1 2y x – 3 1 Reciprocate both sides
  • 51.
    = D C Flipping Equations If it’sadvantageous to do so, we may reposition the equation by reciprocating both sides of an equation. In particular: x = 3 + 1 2y Example D. Solve for y if Literal Equations B A = C D A B x = 3 + 1 2y x – 3 = 1 2y reciprocating both sides, then div. by 2 = 1 2y x – 3 1 = 2y 2(x – 3) 1 Reciprocate both sides 2
  • 52.
    = D C Flipping Equations If it’sadvantageous to do so, we may reposition the equation by reciprocating both sides of an equation. In particular: x = 3 + 1 2y Example D. Solve for y if Literal Equations B A = C D A B x = 3 + 1 2y x – 3 = 1 2y reciprocating both sides, then div. by 2 = 1 2y x – 3 1 = 2y 2(x – 3) 1 Reciprocate both sides 2 = y or 2(x – 3) 1 y =
  • 53.
    Exercise. Solve forthe indicated variables. Literal Equations 1. a – b = d – e for b. 2. a – b = d – e for e. 3. 2*b + d = e for b. 4. a*b + d = e for b. 5. (2 + a)*b + d = e for b. 6. 2L + 2W = P for W 7. (3x + 6)y = 5 for y 8. 3x + 6y = 5 for y w = t – 3 613. for t w = t – b a14. for t w =11. for t w =12. for t t 6 6 t w = 3t – b a15. for t 16. (3x + 6)y = 5 for x w = t – 3 6 17. + a for t w = at – b 5 18. for t w = at – b c 19. + d for t 3 = 4t – b t 20. for t 9. 3x + 6xy = 5 for y 10. 3x – (x + 6)y = 5z for y