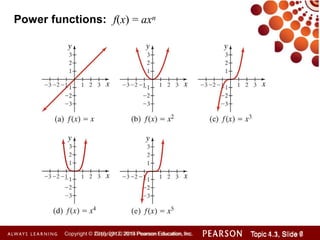
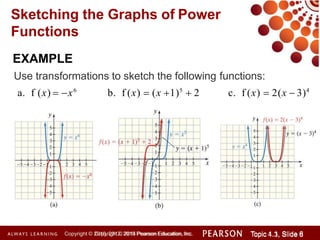
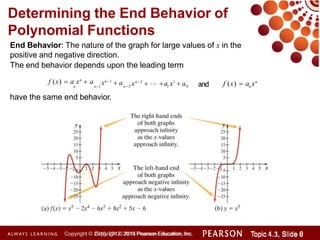
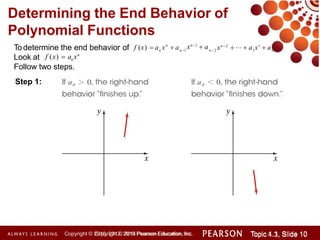
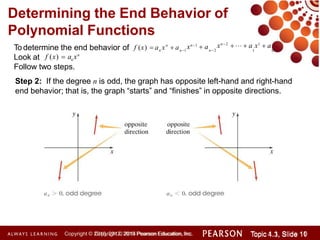
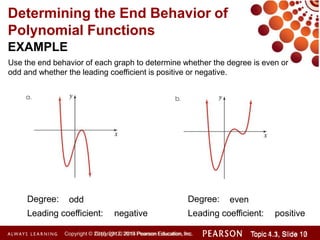
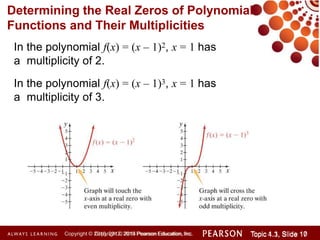
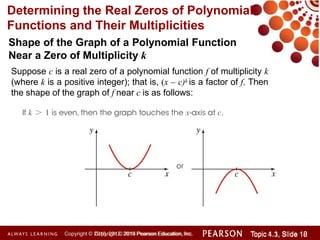
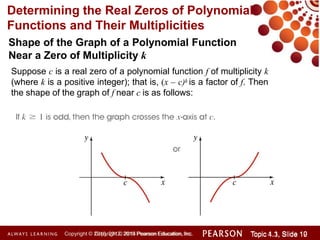
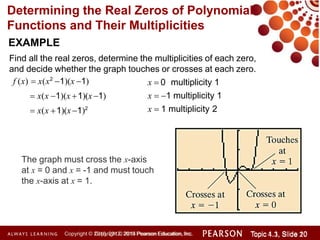
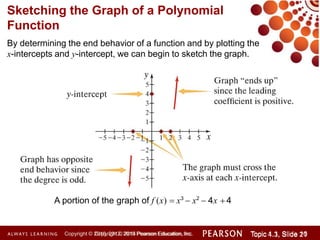
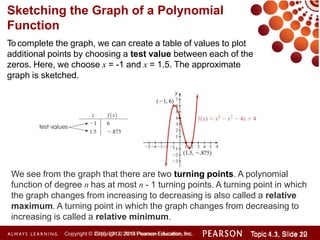
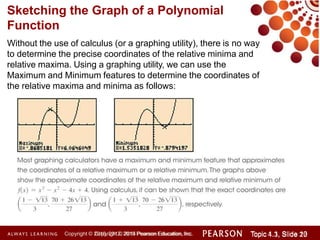
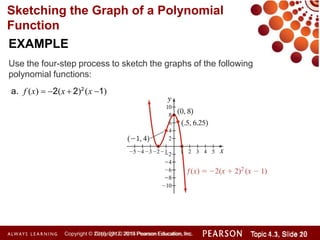
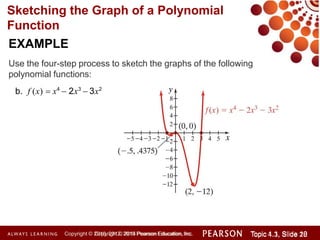
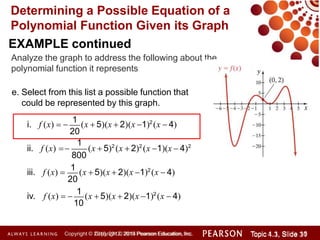
This document discusses polynomial functions and how to graph them. It begins by listing the objectives of understanding the definition of a polynomial function, sketching power functions, determining end behavior, intercepts, real zeros and their multiplicities, and sketching the graph. It then defines polynomial functions and provides examples of determining if a function is polynomial. It also discusses how to sketch power functions, determine end behavior, find intercepts, real zeros and their multiplicities, and use a four step process to sketch the graph of a polynomial function.