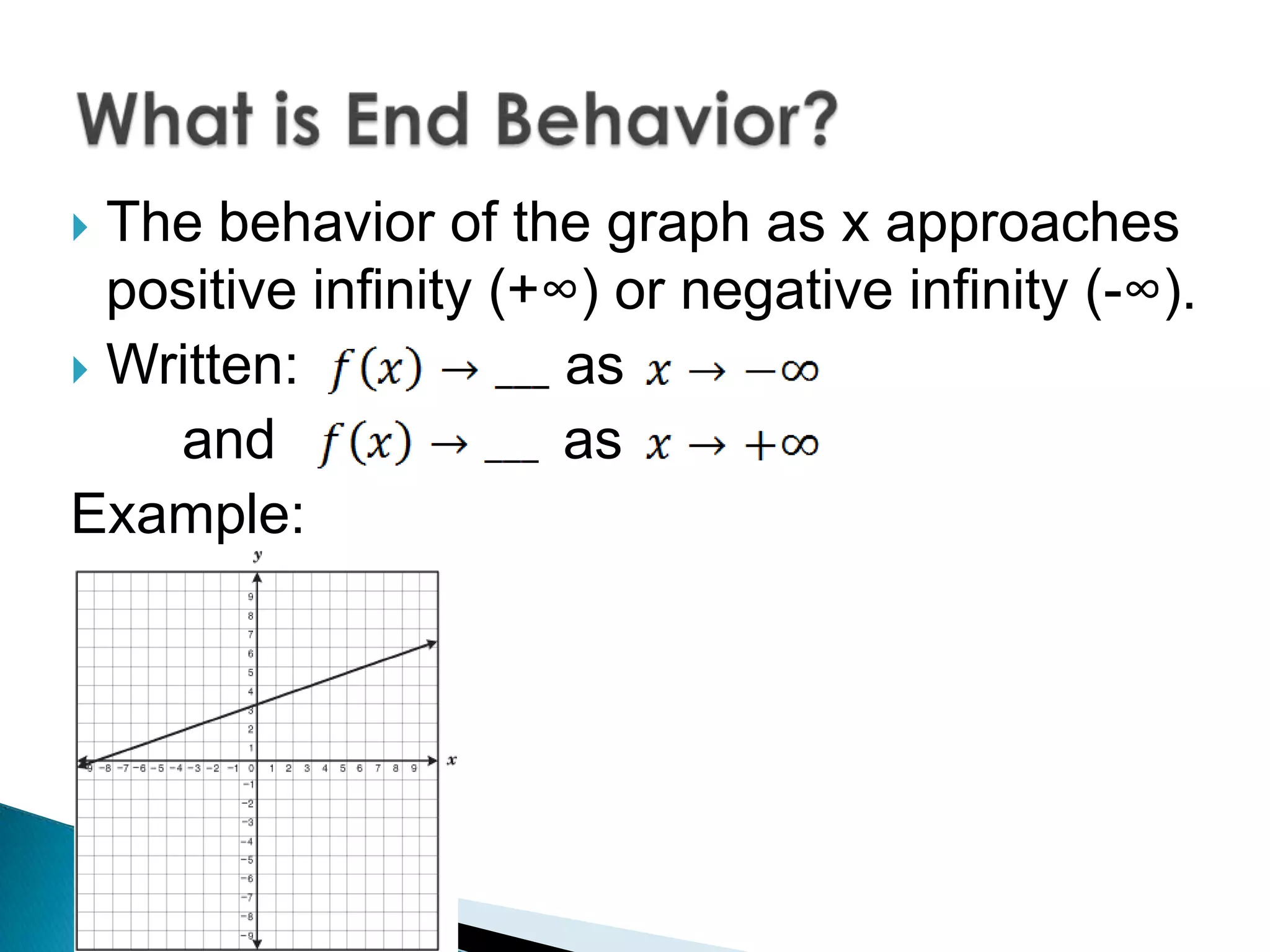
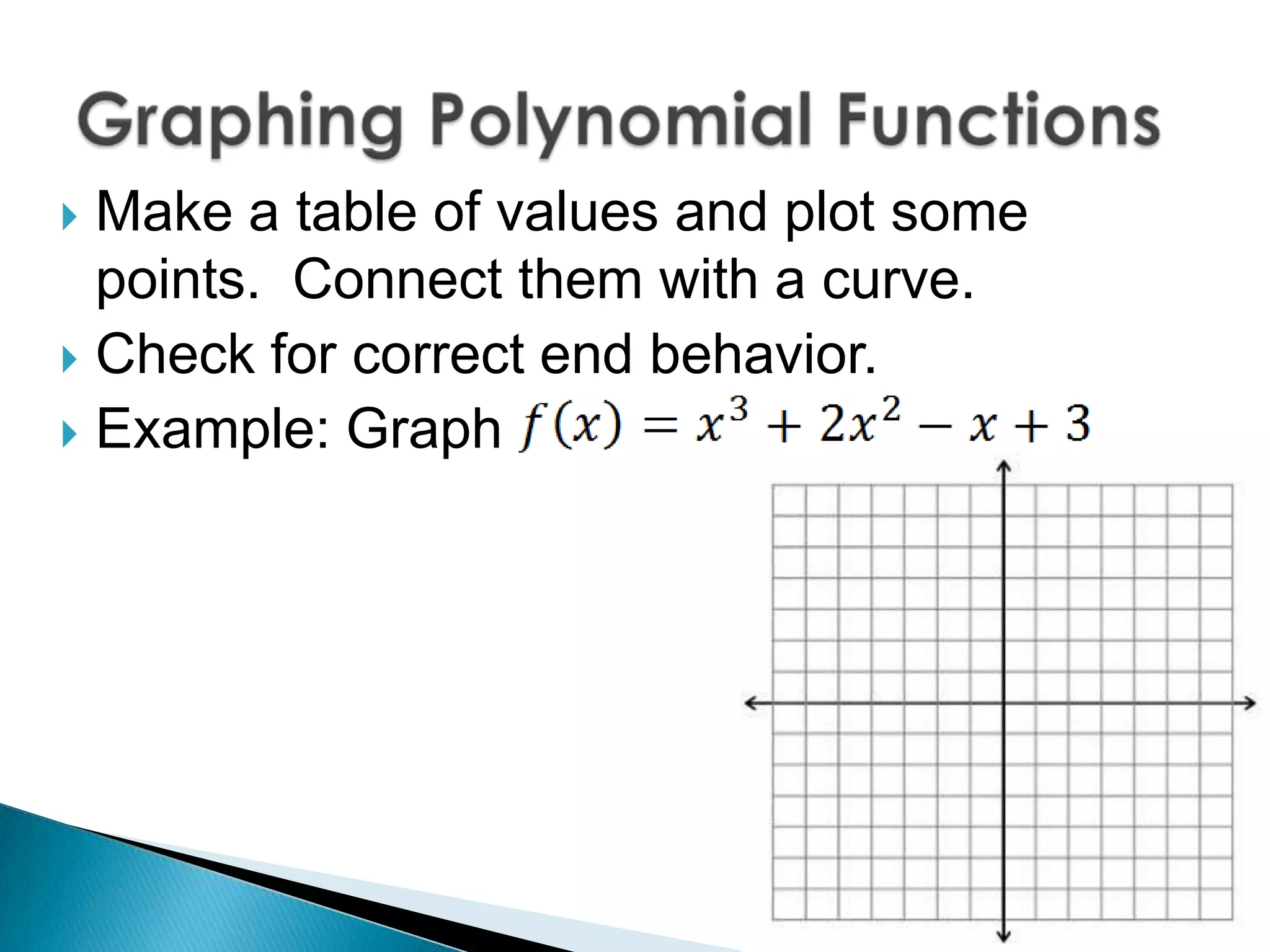
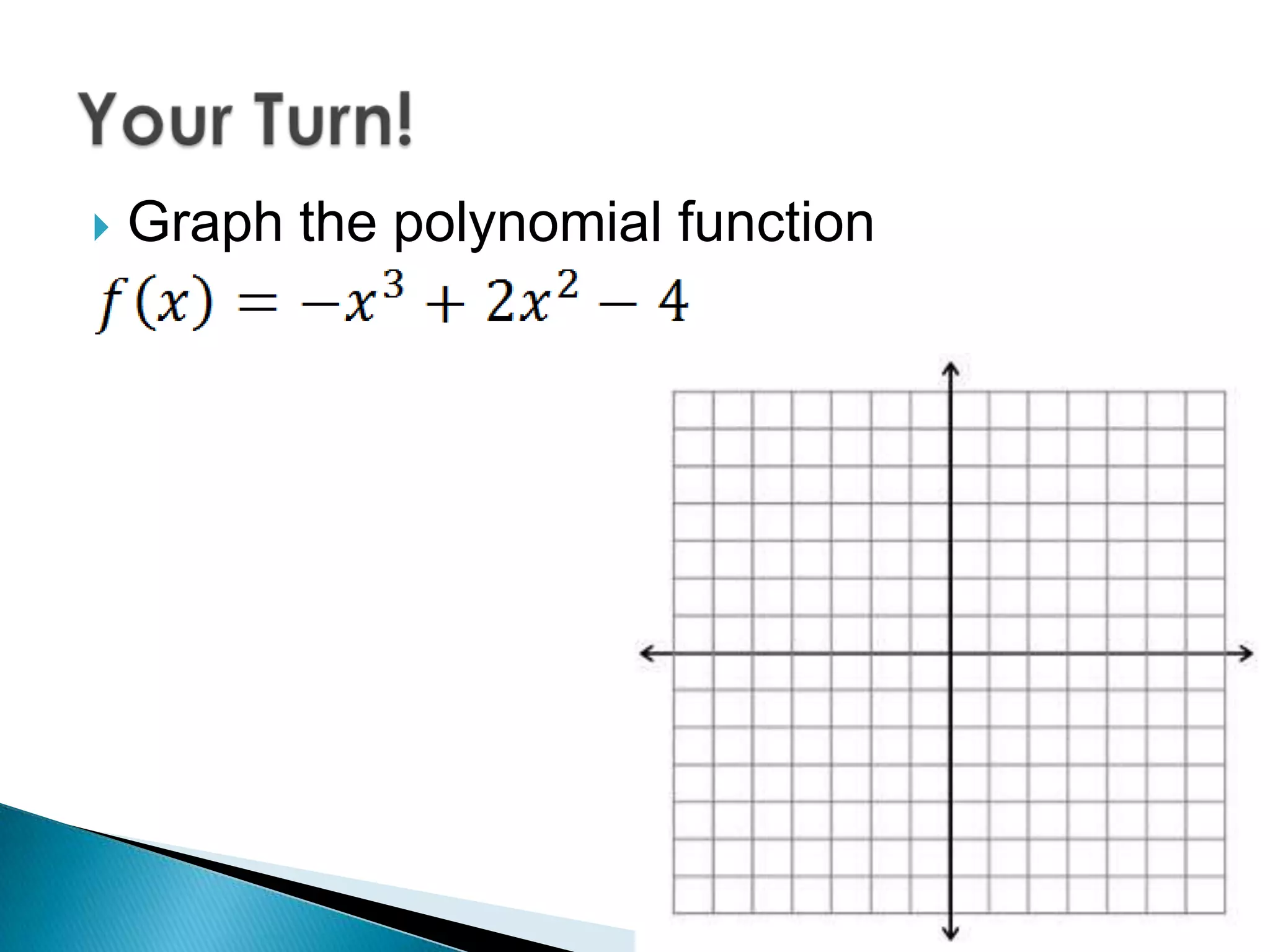
This document discusses how to identify and analyze polynomial functions. It defines polynomials as functions of the form f(x) = anxn + an-1xn-1 + ... + a1x + a0 where the exponents are whole numbers and the coefficients are real numbers. It explains how to determine the degree, type, leading coefficient, and end behavior of polynomial functions. Examples are provided for evaluating polynomials, sketching graphs, and identifying properties from the graphs like the degree, leading coefficient, and number of bumps.

2.  A function of the form:
where , the exponents are all whole
numbers, and the coefficients are all real
numbers.
an is the leading coefficient.
a0 is the constant term.
n is the degree.

3. Degree Type Standard Form
0 Constant
1 Linear
2 Quadratic
3 Cubic
4 Quartic

4.  Determine whether the function is a polynomial.
 If so, write in standard form and identify the
degree, type, and leading coefficient.
 Examples:

5.  Direct Substitution – plug in the given
value for x
 Example: Evaluate
for x = 3.

6.  The behavior of the graph as x approaches
positive infinity (+∞) or negative infinity (-∞).
 Written: as
and as
Example:

7.  Describe the end behavior of the graph.

8.  Write your two functions.
 Sketch a graph of both functions
(use graphing calculator, then copy)
 For each graph, identify:
1. The degree
2. Is the degree odd or even?
3. Leading coefficient (+ or -)
4. End behavior
5. Number of “bumps”/changes in direction

10.  Make a table of values and plot some
points. Connect them with a curve.
 Check for correct end behavior.
 Example: Graph

11.  Graph the polynomial function