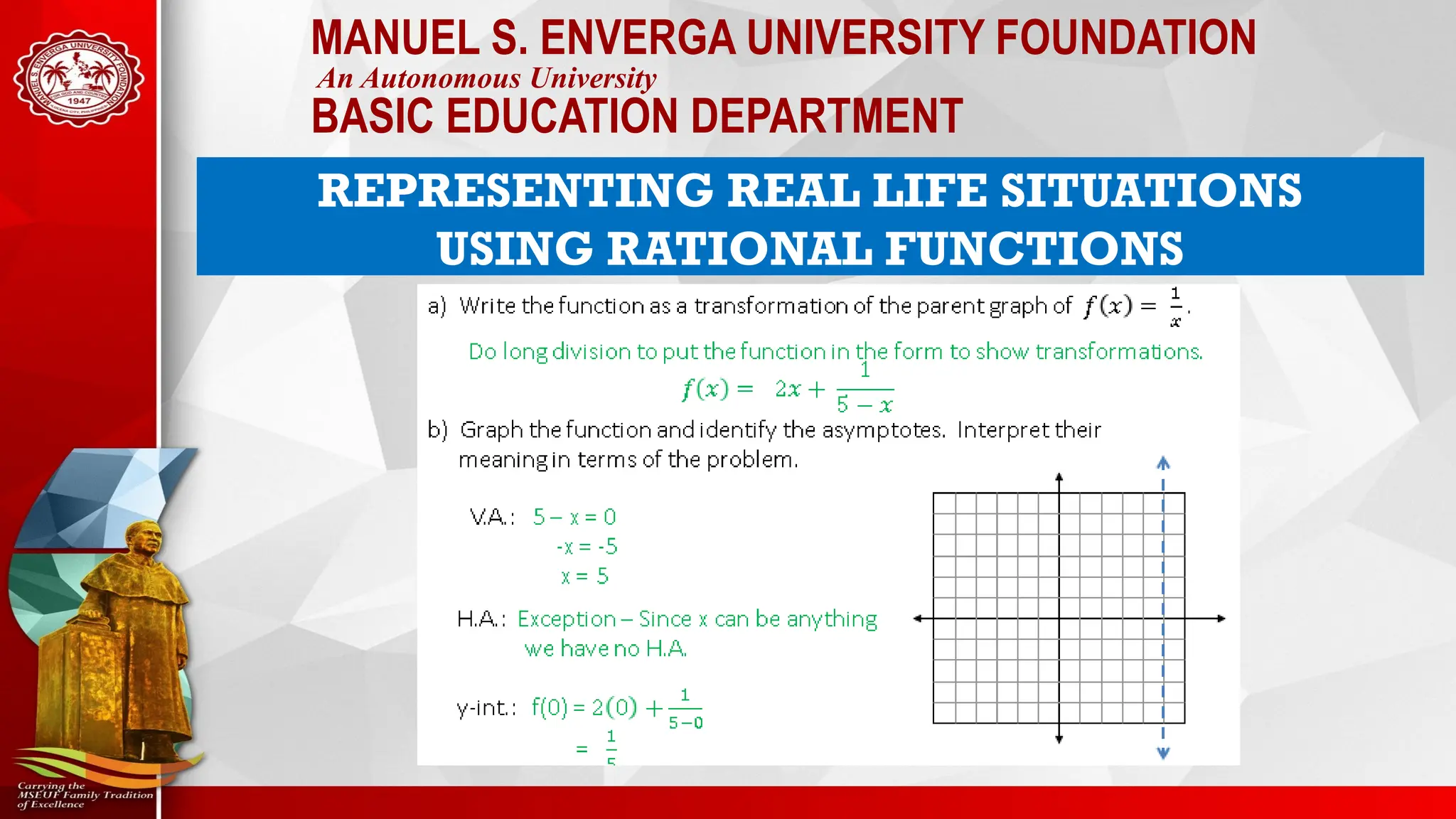
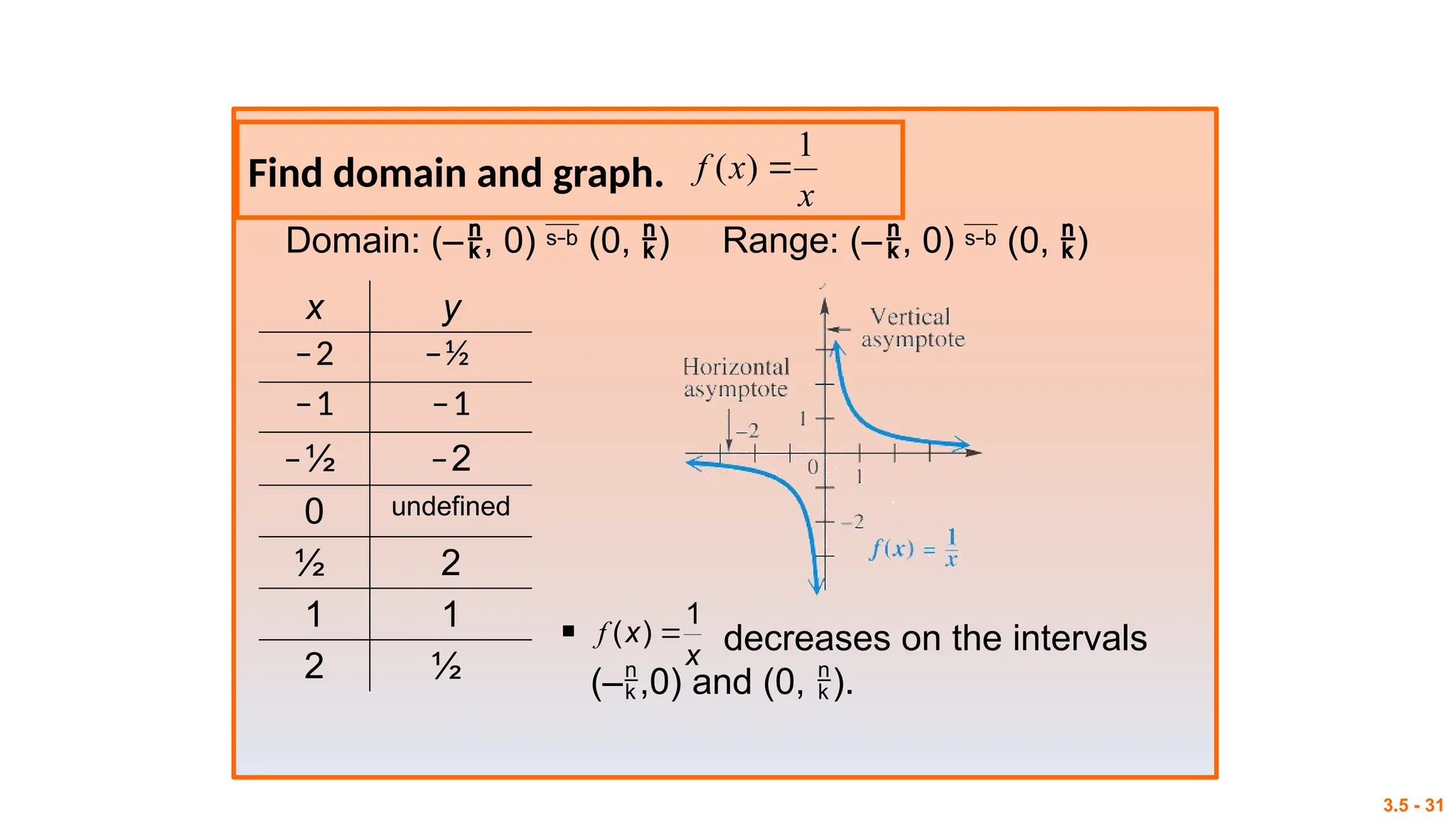
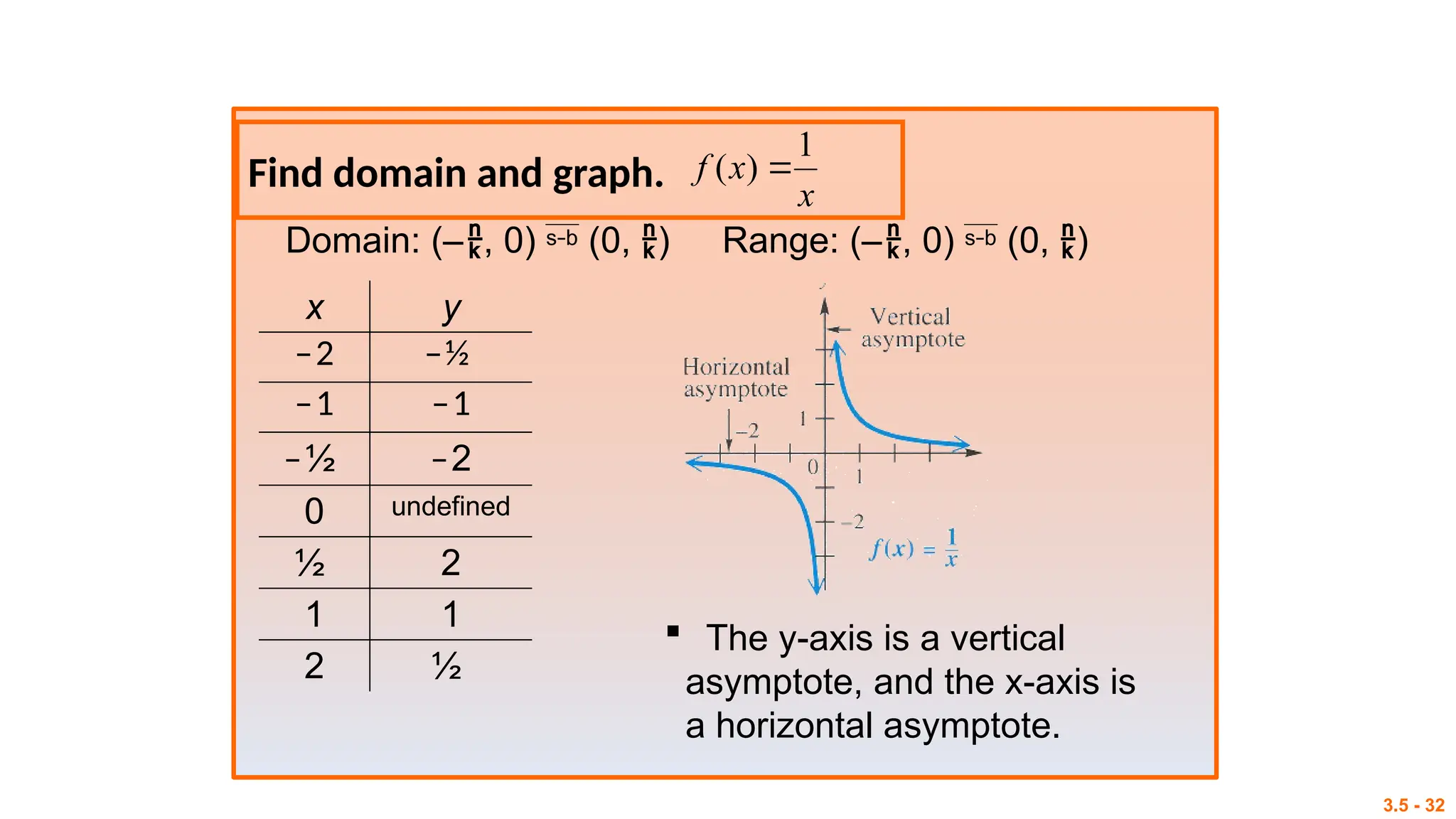
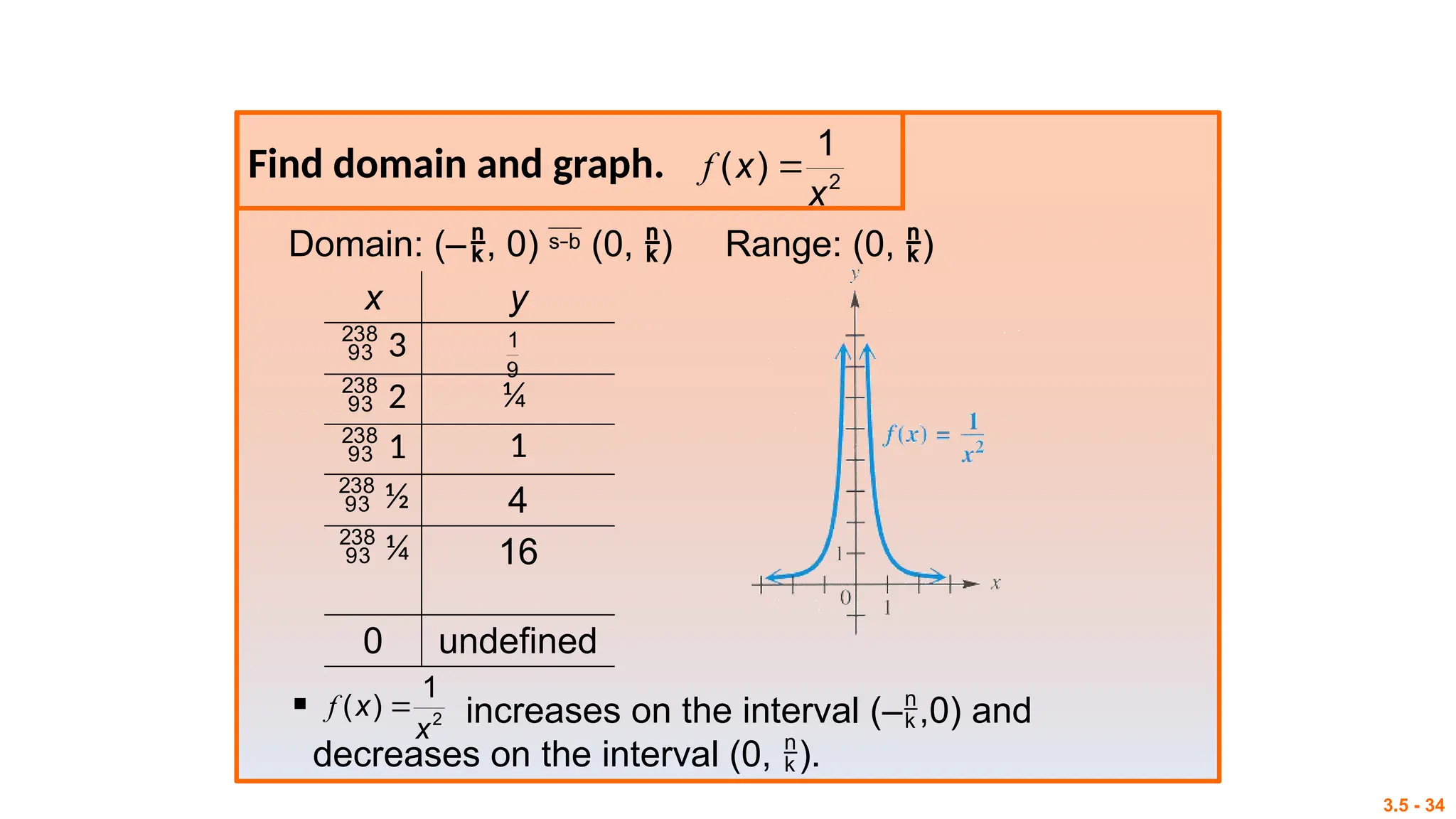
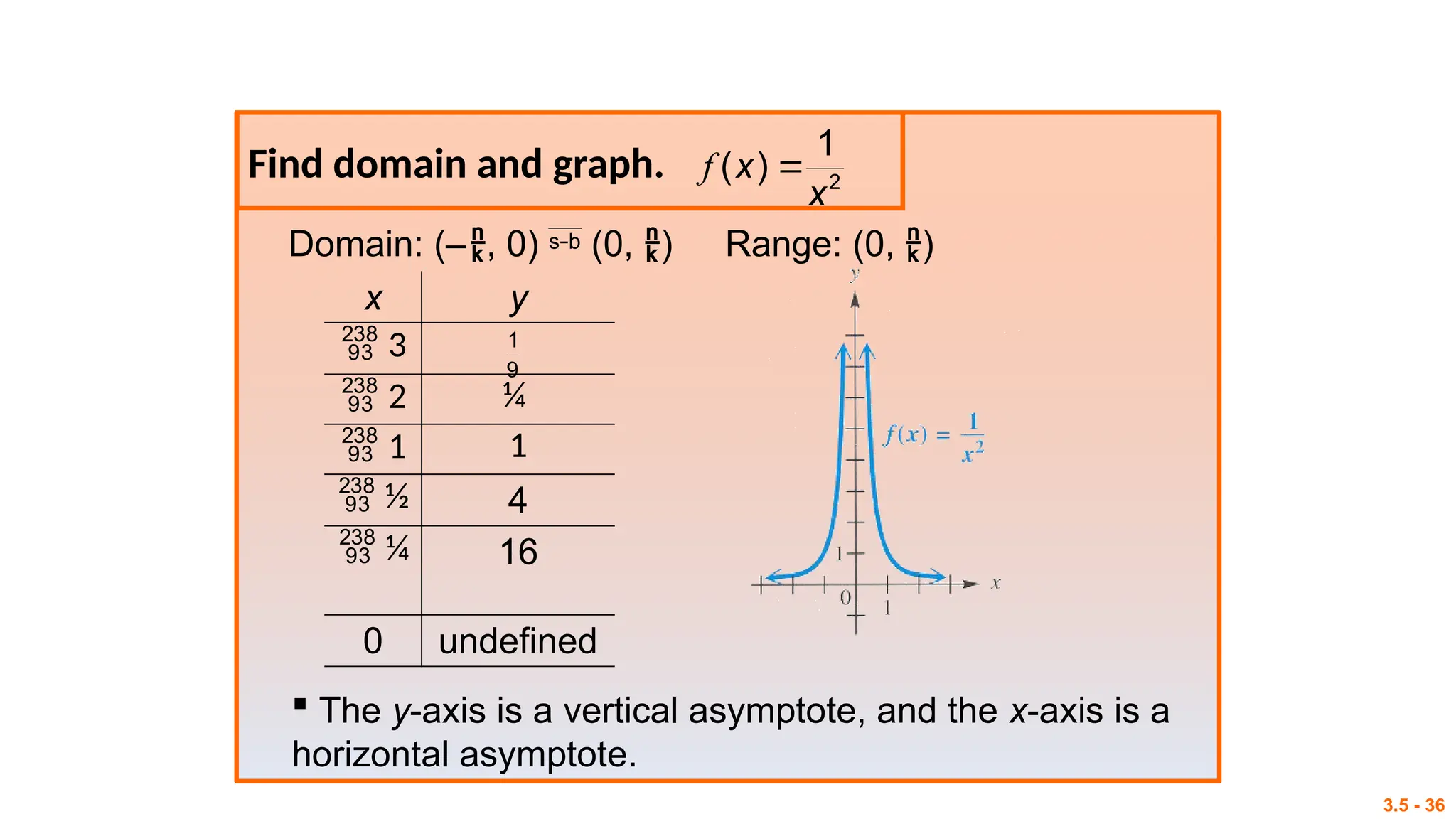
The document outlines session objectives for a mathematics course focused on rational functions, including representation of real-life situations, solving equations, and graphing techniques. It covers key concepts like vertical and horizontal asymptotes, domain and range, and includes various activities and analysis tasks for students. Conclusively, it aims to equip learners with problem-solving skills related to rational, exponential, and logarithmic functions.