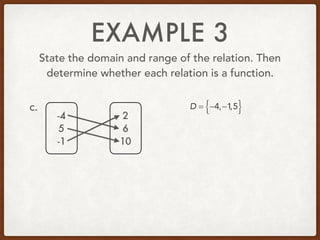
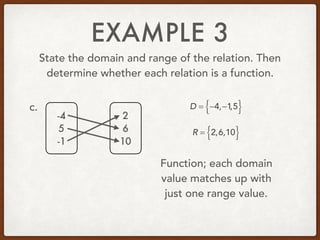
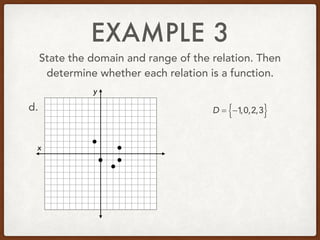
The document discusses identifying the domain and range of functions. The domain is the set of all x-coordinates in a relation, while the range is the set of all y-coordinates. A relation is a function if each element in the domain is mapped to only one element in the range - in other words, if each x-value has a single, unique y-value. The document provides examples of stating the domain and range of relations and determining whether they represent functions.

1. REPRESENTING
FUNCTIONS
SECTION 0-1

2. ESSENTIAL QUESTION
How do you identify the domain and range of functions?

3. VOCABULARY
1. Domain:
2. Range:
3. Quadrants:
4. Mapping:
5. Function:

4. VOCABULARY
1. Domain:
2. Range:
3. Quadrants:
4. Mapping:
5. Function:
The set of all of the x-coordinates in a relation

5. VOCABULARY
1. Domain:
2. Range:
3. Quadrants:
4. Mapping:
5. Function:
The set of all of the x-coordinates in a relation
The set of all of the y-coordinates in a relation

6. VOCABULARY
1. Domain:
2. Range:
3. Quadrants:
4. Mapping:
5. Function:
The set of all of the x-coordinates in a relation
The set of all of the y-coordinates in a relation
The four areas created by the x-axis and
y-axis; Quadrant I is where everything is positive,
then rotate counterclockwise to name the rest

7. VOCABULARY
1. Domain:
2. Range:
3. Quadrants:
4. Mapping:
5. Function:
The set of all of the x-coordinates in a relation
The set of all of the y-coordinates in a relation
The four areas created by the x-axis and
y-axis; Quadrant I is where everything is positive,
then rotate counterclockwise to name the rest
Shows how each element in the domain
is paired with an element in the range

8. VOCABULARY
1. Domain:
2. Range:
3. Quadrants:
4. Mapping:
5. Function:
The set of all of the x-coordinates in a relation
The set of all of the y-coordinates in a relation
The four areas created by the x-axis and
y-axis; Quadrant I is where everything is positive,
then rotate counterclockwise to name the rest
Shows how each element in the domain
is paired with an element in the range
Each element in the domain matches with
only one element in the range.

9. EXAMPLE 1
State the domain and range of the relation. Does this
relation represent a function?
−2,−1( ), −1,0( ), 1,−5( ), 2,7( ){ }

10. EXAMPLE 1
State the domain and range of the relation. Does this
relation represent a function?
−2,−1( ), −1,0( ), 1,−5( ), 2,7( ){ }
D = −2,−1,1,2{ }

11. EXAMPLE 1
State the domain and range of the relation. Does this
relation represent a function?
−2,−1( ), −1,0( ), 1,−5( ), 2,7( ){ }
D = −2,−1,1,2{ } R = −5,−1,0,7{ }

12. EXAMPLE 1
State the domain and range of the relation. Does this
relation represent a function?
−2,−1( ), −1,0( ), 1,−5( ), 2,7( ){ }
D = −2,−1,1,2{ } R = −5,−1,0,7{ }
Yes, this is a function. Each value in the domain only
matches with one value in the range.

13. EXAMPLE 2
Name the quadrant in which P(2, -6) is located.
x
y

14. EXAMPLE 2
Name the quadrant in which P(2, -6) is located.
x
y
I

15. EXAMPLE 2
Name the quadrant in which P(2, -6) is located.
x
y
III

16. EXAMPLE 2
Name the quadrant in which P(2, -6) is located.
x
y
III
III

17. EXAMPLE 2
Name the quadrant in which P(2, -6) is located.
x
y
III
III IV

18. EXAMPLE 2
Name the quadrant in which P(2, -6) is located.
x
y
III
III IVP

19. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
3,2( ), 4,1( ), 6,2( ), 8,0( ){ }a.

20. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
3,2( ), 4,1( ), 6,2( ), 8,0( ){ }a.
D = 3,4,6,8{ }

21. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
3,2( ), 4,1( ), 6,2( ), 8,0( ){ }a.
D = 3,4,6,8{ }
R = 0,1,2{ }

22. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
3,2( ), 4,1( ), 6,2( ), 8,0( ){ }a.
D = 3,4,6,8{ }
R = 0,1,2{ }
Function; each domain
value matches up with
just one range value.

23. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
b. x y
0 -2
3 2
6 2

24. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
b. x y
0 -2
3 2
6 2
D = 0,3,6{ }

25. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
b. x y
0 -2
3 2
6 2
D = 0,3,6{ }
R = −2,2{ }

26. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
b. x y
0 -2
3 2
6 2
D = 0,3,6{ }
R = −2,2{ }
Function; each domain
value matches up with
just one range value.

27. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
c.
-4
5
-1
2
6
10
x y

28. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
c. D = −4,−1,5{ }
-4
5
-1
2
6
10
x y

29. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
c. D = −4,−1,5{ }
R = 2,6,10{ }
-4
5
-1
2
6
10
x y

30. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
c. D = −4,−1,5{ }
R = 2,6,10{ }
Function; each domain
value matches up with
just one range value.
-4
5
-1
2
6
10
x y

31. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
d.
x
y

32. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
d. D = −2,0,2,3{ }
x
y

33. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
d. D = −2,0,2,3{ }
R = −2,−1,1,2{ }
x
y

34. EXAMPLE 3
State the domain and range of the relation. Then
determine whether each relation is a function.
d. D = −2,0,2,3{ }
R = −2,−1,1,2{ }
Not a function; when
the domain value is 3,
there are two possible
range values
x
y

35. SUMMARY
What are the domain and range of a relation?
How do you know whether a relation is a function?