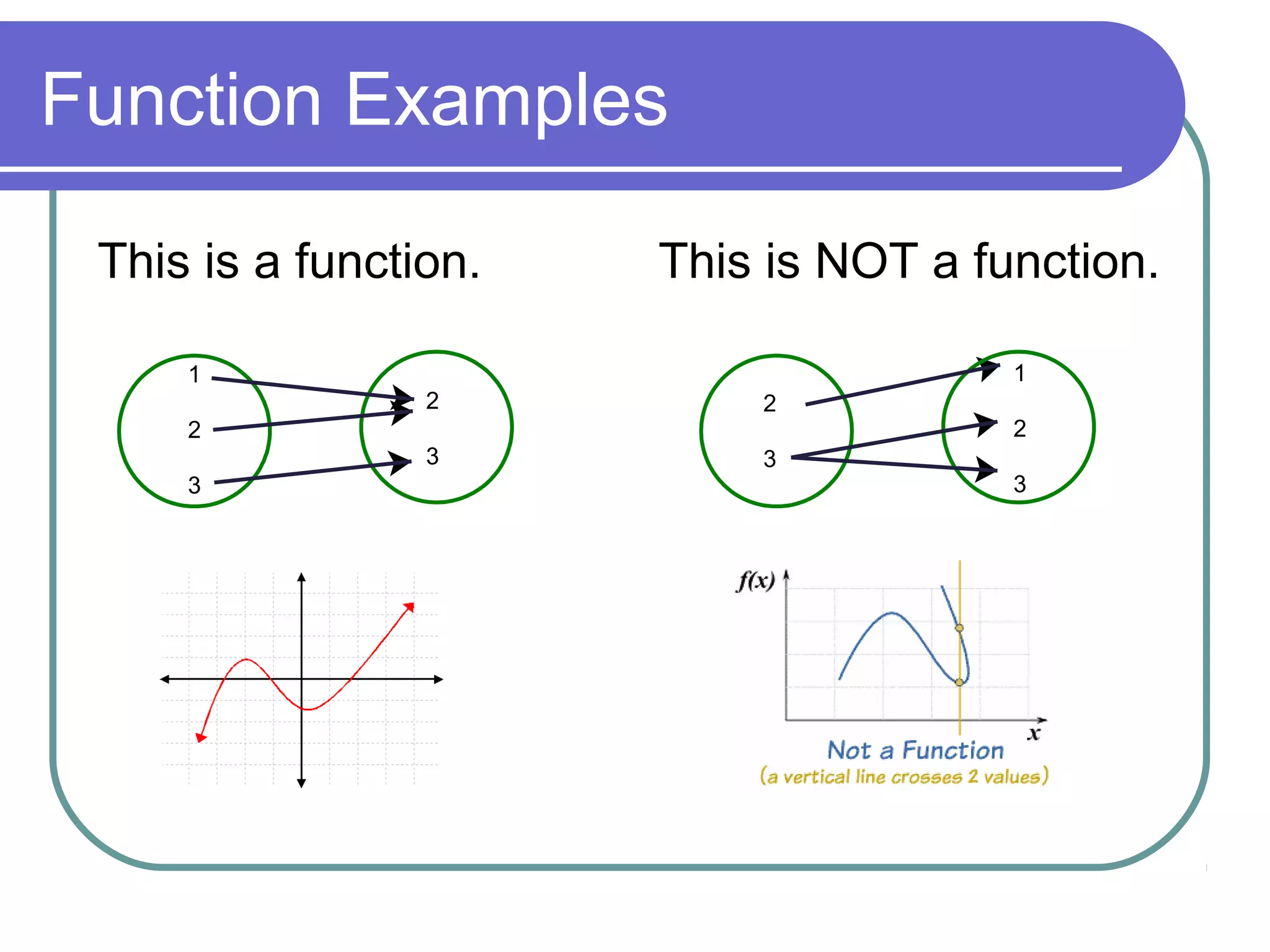
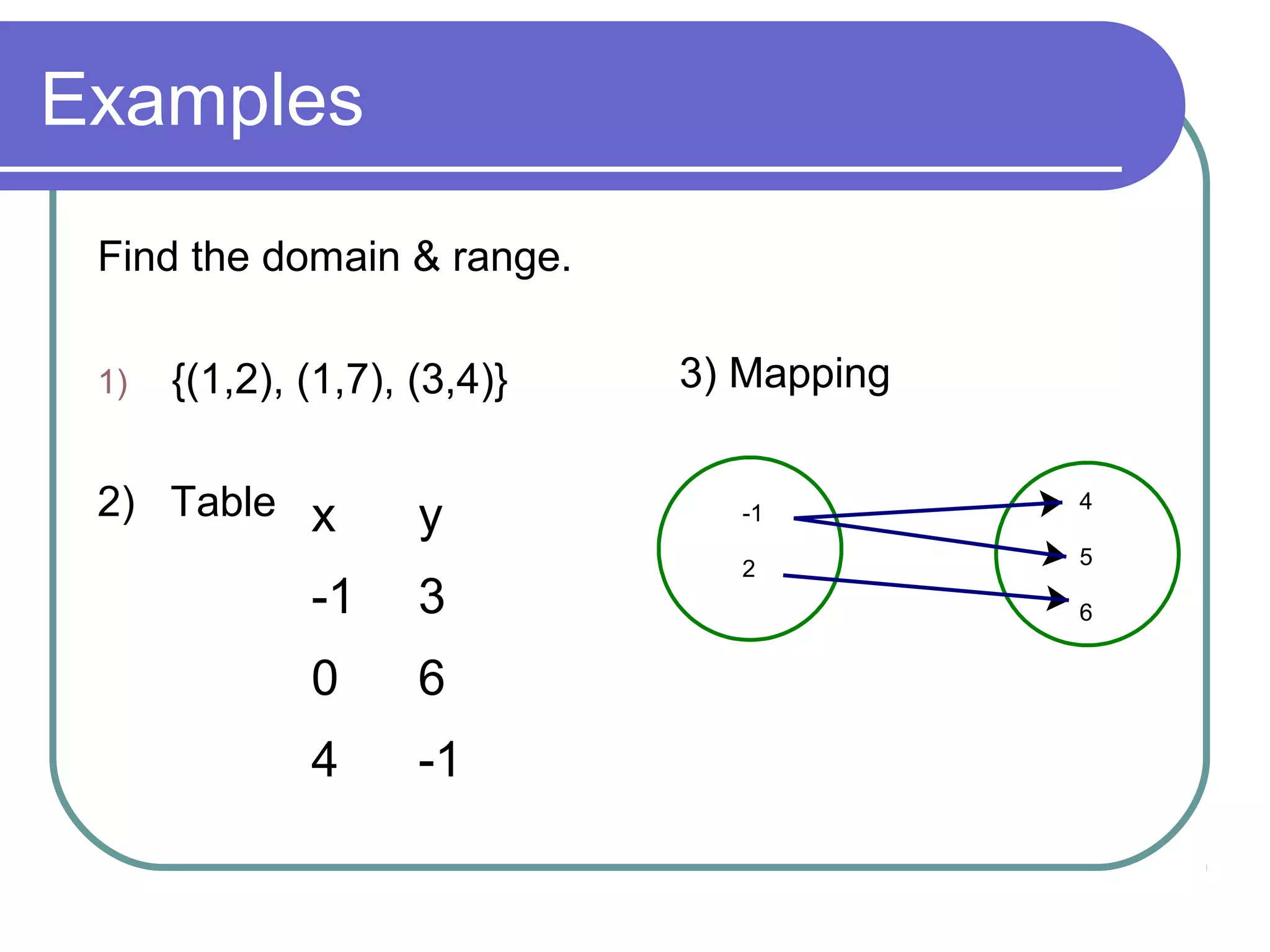
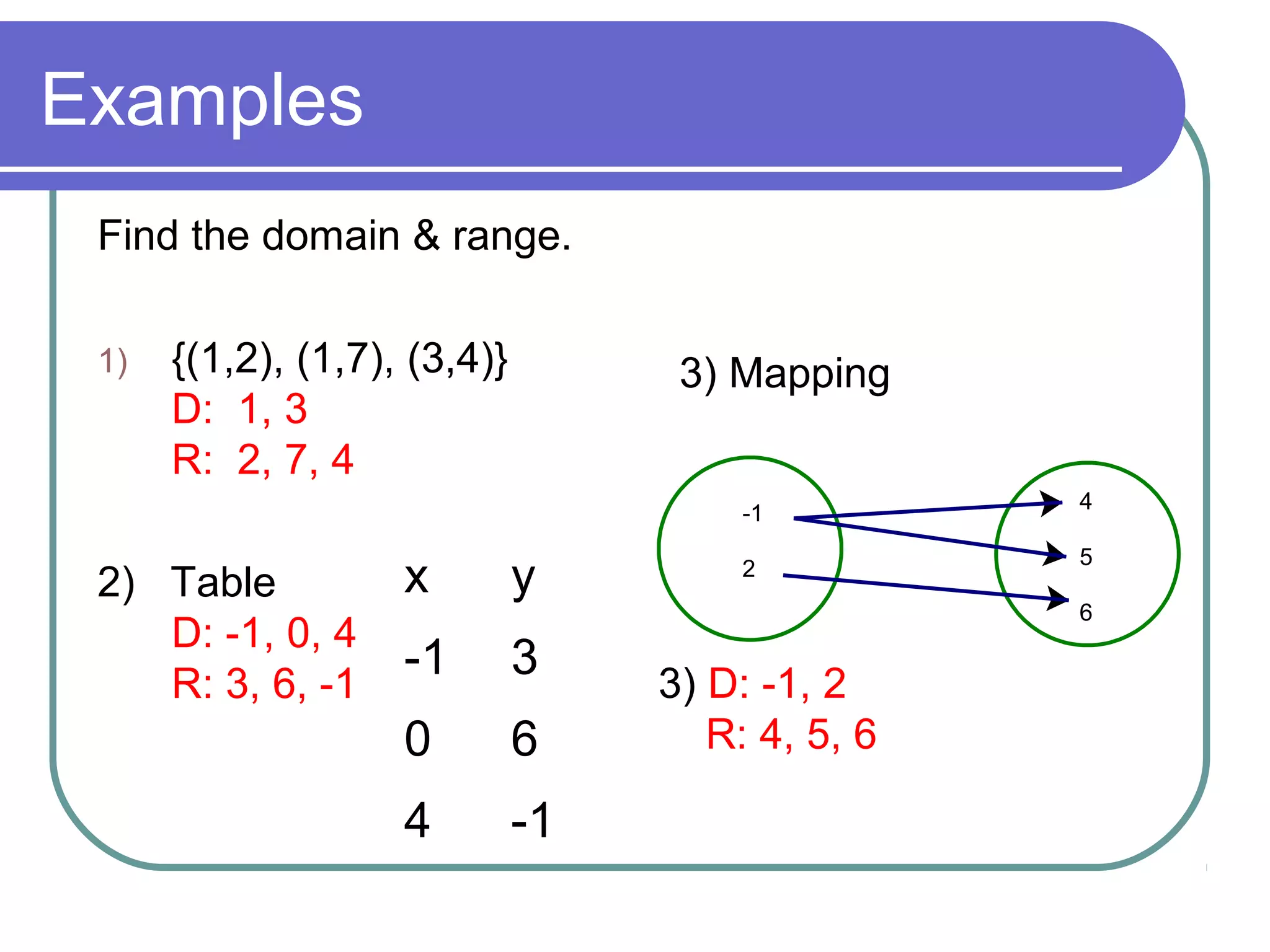
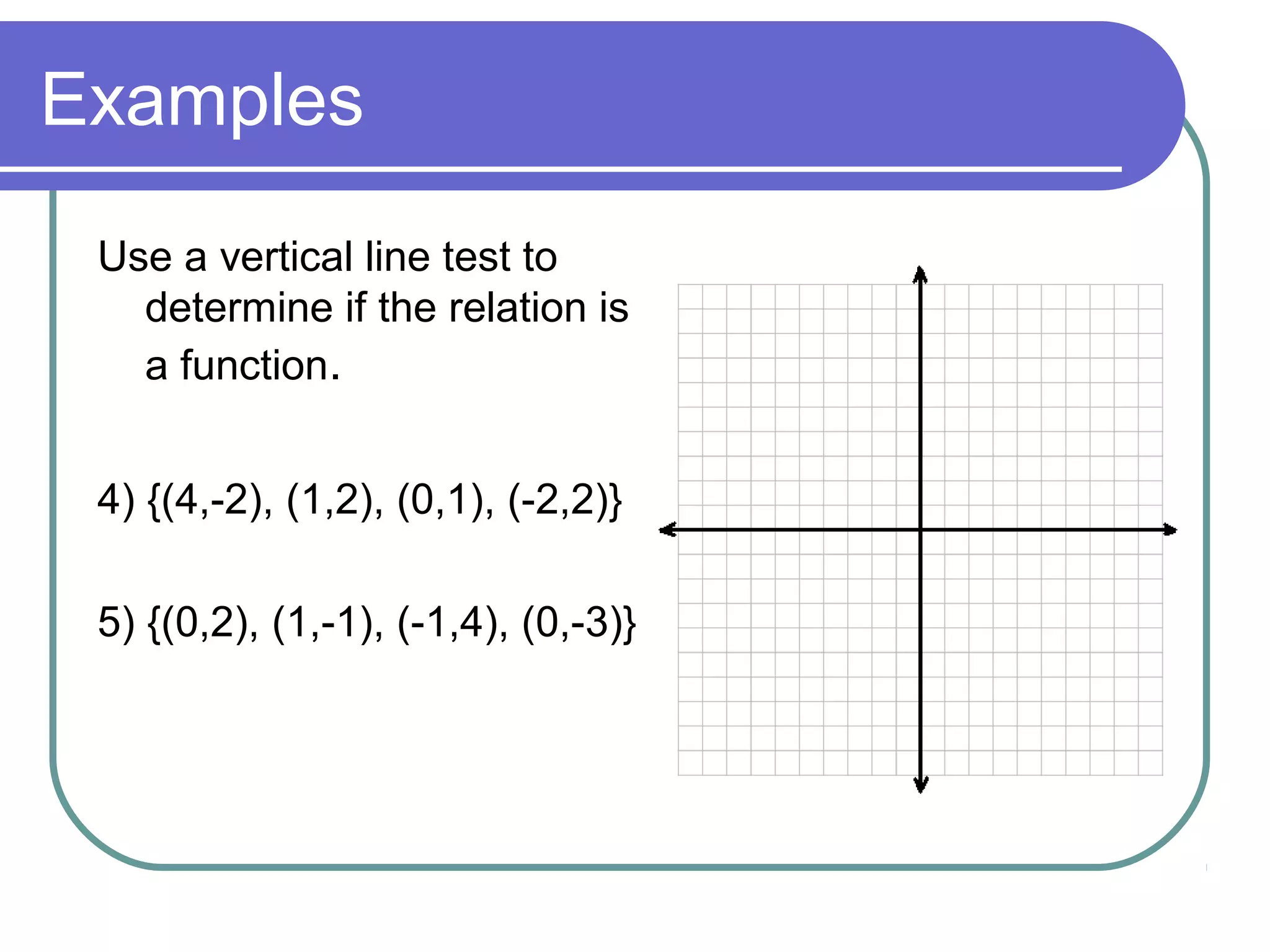
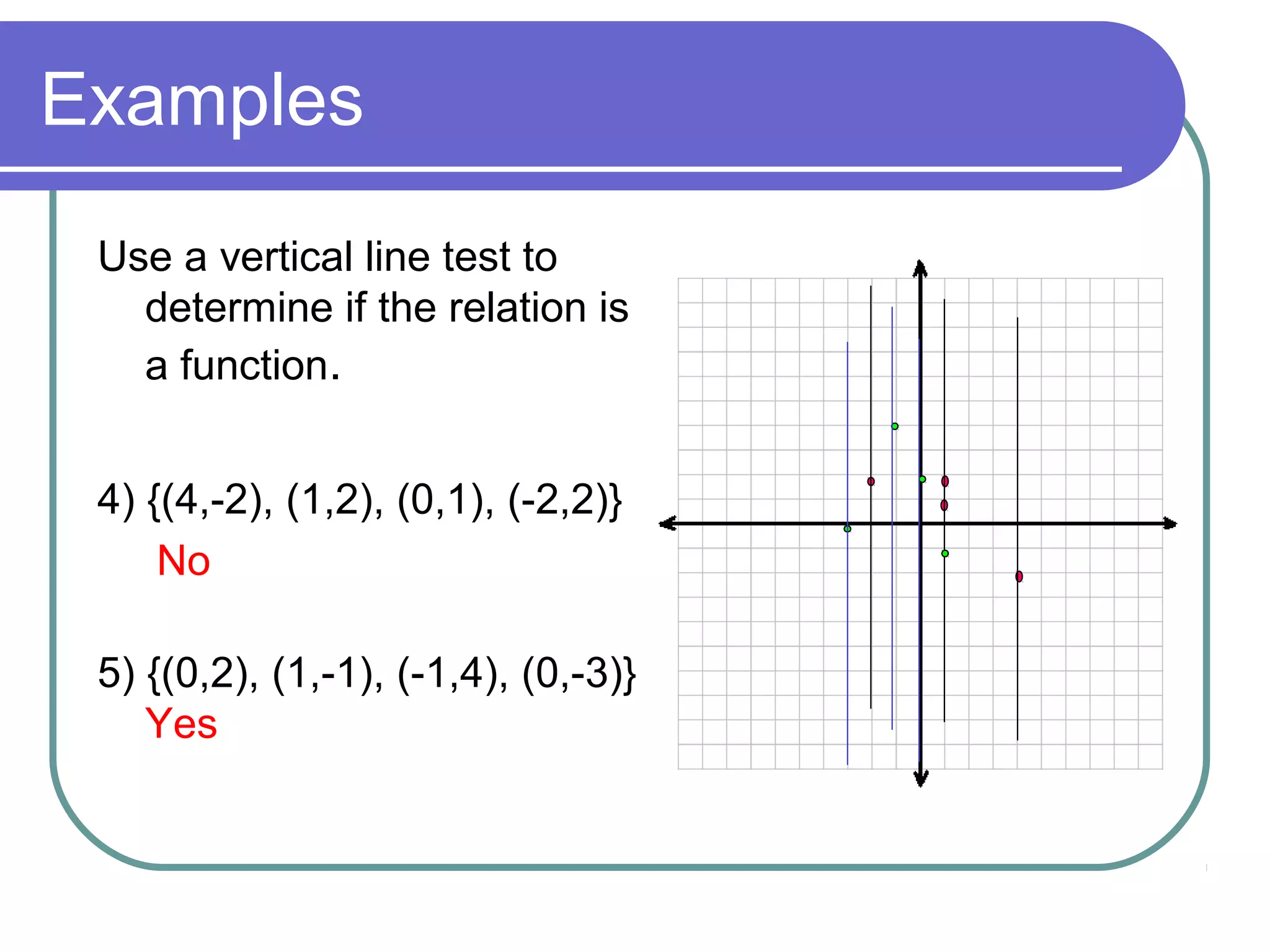
The document summarizes key concepts about relations and functions including: 1) It defines relation, domain, range, and function. 2) It provides examples of relations that are and are not functions using ordered pairs, tables, and mappings. 3) It shows how to determine if a relation is a function using a vertical line test and mappings. 4) It gives examples of finding the domain and range of relations and determining if other relations are functions.

1. Math 2
Relations and Functions
Function Rules, Tables & Graphs

2. Vocabulary
Relation – set of ordered pairs
Domain – x values
Range – y values
Function – relation that assigns exactly
one value in the range to each value in
the domain

3. Function Examples
This is a function. This is NOT a function.
1
2
3
2
3
1
2
3
2
3

4. Examples
Find the domain & range.
1) {(1,2), (1,7), (3,4)}
2) Table x y
-1 3
0 6
4 -1
3) Mapping
4
5
6
-1
2

5. Examples
Find the domain & range.
1) {(1,2), (1,7), (3,4)}
D: 1, 3
R: 2, 7, 4
2) Table
D: -1, 0, 4
R: 3, 6, -1
x y
-1 3
0 6
4 -1
3) Mapping
4
5
6
-1
2
3) D: -1, 2
R: 4, 5, 6

6. Examples
Use a vertical line test to
determine if the relation is
a function.
4) {(4,-2), (1,2), (0,1), (-2,2)}
5) {(0,2), (1,-1), (-1,4), (0,-3)}

7. Examples
Use a vertical line test to
determine if the relation is
a function.
4) {(4,-2), (1,2), (0,1), (-2,2)}
No
5) {(0,2), (1,-1), (-1,4), (0,-3)}
Yes

8. Examples
Use a mapping to
determine if the relation
is a function.
6) {(3,-2), (8,1), (9,2), (3,3)}
7) {(6,0), (7,-1), (6,0), (2,6)}
Find the range if the
domain is {-4, -2, 0, 4}.
8) y = -2x + 1
9) f(x) = 3x – 7
10) y = x3
+ 2

9. Examples
Model the rule with a table and a graph.
Use D={ -2, -1, 0, 1, 5}
11)f(x) = 3x + 4 12) f(x) = |x| - 1

10. Examples
Model the rule with a table and a graph.
Use D={ -2, -1, 0, 1, 5}
13) y = x2
– 1 14) y = 8 - x