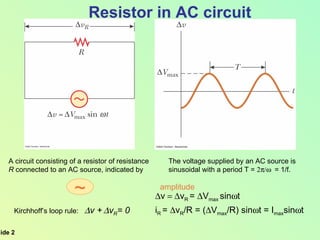
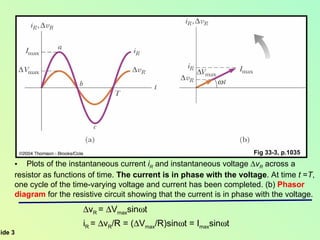
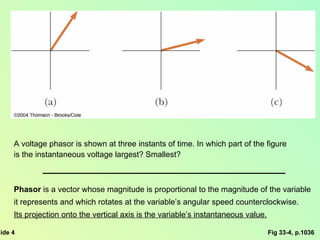
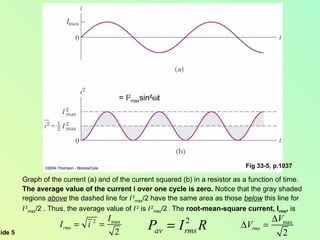
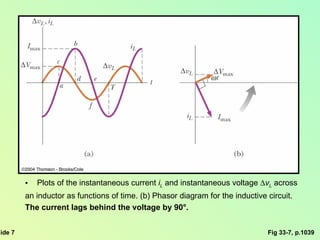
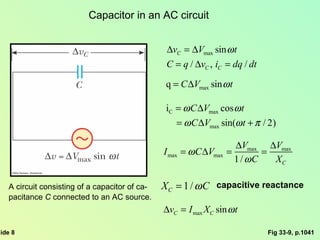
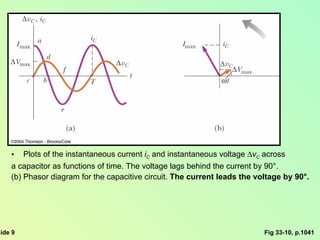
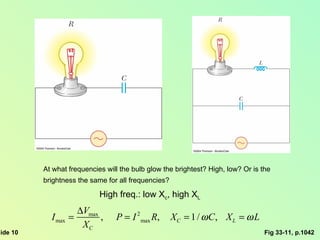
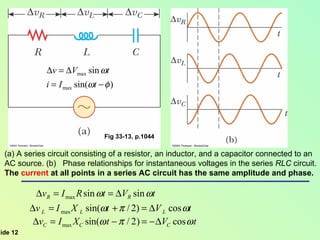
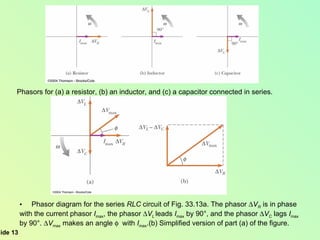
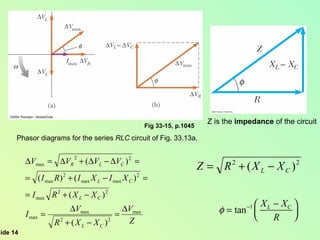
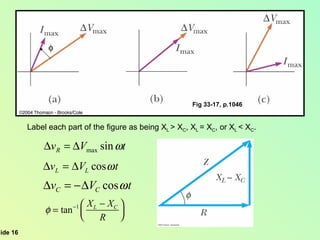
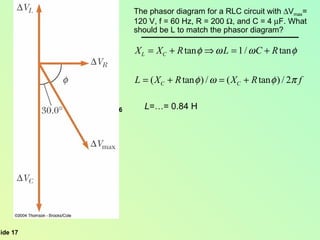
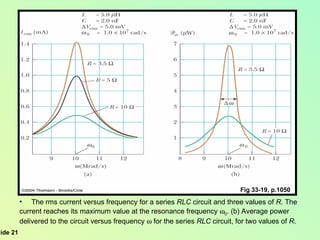
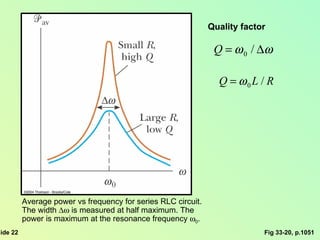
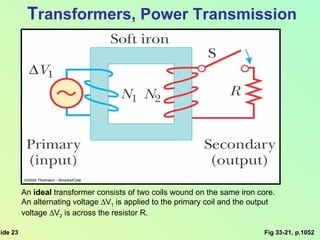
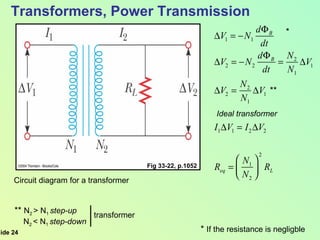
This document summarizes key concepts about alternating current (AC) circuits including resistors, inductors, and capacitors in AC circuits. It discusses the RLC series circuit, power in AC circuits, and resonance. It also covers transformers and how they are used for power transmission by stepping voltages up or down. Resonance occurs at the resonance frequency when the inductive reactance equals the capacitive reactance in a RLC series circuit, resulting in maximum current. Transformers use magnetic induction to change AC voltages efficiently for applications like power distribution.

2. The voltage supplied by an AC source is sinusoidal with a period T =  = 1/f. A circuit consisting of a resistor of resistance R connected to an AC source, indicated by Resistor in AC circuit  v  v R =  V max sin  t i R =  v R /R = (  V max /R) sin  t = I max sin  t Kirchhoff’s loop rule:  v +  v R = 0 amplitude ~

4. Fig 33-4, p.1036 A voltage phasor is shown at three instants of time. In which part of the figure is the instantaneous voltage largest? Smallest? Phasor is a vector whose magnitude is proportional to the magnitude of the variable it represents and which rotates at the variable’s angular speed counterclockwise. Its projection onto the vertical axis is the variable’s instantaneous value.

5. Fig 33-5, p.1037 Graph of the current (a) and of the current squared (b) in a resistor as a function of time. The average value of the current i over one cycle is zero. Notice that the gray shaded regions above the dashed line for I 2 max /2 have the same area as those below this line for I 2 max /2 . Thus, the average value of I 2 is I 2 max /2 . The root-mean-square current, I rms , is = I 2 max sin 2  t

6. Fig 33-6, p.1038 A circuit consisting of an inductor of inductance L connected to an AC source. inductive reactance Inductors in an AC circuit Kirchhoff’s law Instantaneous current in the inductor

8. Fig 33-9, p.1041 A circuit consisting of a capacitor of ca- pacitance C connected to an AC source. capacitive reactance Capacitor in an AC circuit

10. Fig 33-11, p.1042 At what frequencies will the bulb glow the brightest? High, low? Or is the brightness the same for all frequencies? High freq.: low X c , high X L

14. Fig 33-15, p.1045 Phasor diagrams for the series RLC circuit of Fig. 33.13a. Z is the impedance of the circuit

16. Fig 33-17, p.1046 Label each part of the figure as being X L > X C , X L = X C , or X L < X C . 

17. Fig 33-18, p.1046 The phasor diagram for a RLC circuit with  V max = 120 V, f = 60 Hz, R = 200  , and C = 4  F. What should be L to match the phasor diagram? L =…= 0.84 H

18. A series RLC circuit has  V max =150 V,  = 377 s -1 Hz, R= 425  , L= 1.25 H, and C = 3.5  F. Find its Z, X C , X L , I max , the angle  between current and voltage, and the maximum and instantaneous voltages across each element. X C = 471  X L = 758  Z = 513  I max = 0.292 A  = -34 o

19. Power in an AC Circuit The average power delivered by the source is converted to internal energy in the resistor Pure resistive load:  = 0  No power losses are associated with pure capacitors and pure inductors in an AC circuit ( ) Momentary values, average is 0

20. Resonance in a Series RLC Circuit A series RLC circuit is in resonance when the current has its maximum value The resonance frequency  0 is obtained from X L = X C ,  L= 1/  C : At resonance, when  0 , the average power is maximum and has the value

22. Fig 33-20, p.1051 Quality factor Average power vs frequency for series RLC circuit. The width  is measured at half maximum. The power is maximum at the resonance frequency  0 .

23. Fig 33-21, p.1052 An ideal transformer consists of two coils wound on the same iron core. An alternating voltage  V 1 is applied to the primary coil and the output voltage  V 2 is across the resistor R. T ransformers, Power Transmission

24. Fig 33-22, p.1052 Circuit diagram for a transformer ** ** N 2 > N 1 step-up N 2 < N 1 step-down transformer Transformers, Power Transmission Ideal transformer * * If the resistance is negligble

25. p.1053 Nikola Tesla (1856–1943), American Physicist

26. Fig 33-23, p.1053 The primary winding in this transformer is attached to the prongs of the plug. The secondary winding is connected to the wire on the right, which runs to an electronic device. (120-V to 12.5-V AC) Many of these power-supply transformers also convert alternating current to direct current.

27. p.1053 This transformer is smaller than the one in the opening photograph for this chapter. In addition, it is a step-down transformer. It drops the voltage from 4 000 V to 240 V for delivery to a group of residences.